Образец протокола №2 эксперимента по методу «да-нет»

Протокол № 2 2 серия

Порядковый номер пробы	Вид пробы	Ответ испытуемого	Исход пробы
1	S	нет	N/S – пропуск стимула
2	n	Да	Y/n – ложная тревога
3	S	да	Y/S – правильное обнаружение
4	n	нет	N/n – правильное отрицание
5	S	нет	N/S – пропуск стимула
. . .	. . .	. . .	. . .
200	S	да	Y/S – правильное обнаружение
	(S) = 150 (n) = 50		(Y/S) = обн = 119 (Y/n) = лт = 24

Используя алгоритм, уже применявшийся для расчетов P_обн и P_лт в первой серии, во второй серии получаем:

P_обн = = 0,79;

P_лт = = 0,48.

Таким образом, изменив значение априорных вероятностей появления стимула в пробе q_(S) и его отсутствия q_(n), получаем увеличение и P_обн, и одновременно P_лт, что совершенно закономерно.

2) Построение графика px.

Графически построение PX возможно двумя способами:

а) в линейных координатах (по оси x - P_лт, по оси y - P_обн);

b) в Z-координатах (так называемых «двойных нормальных» координатах: по оси x - Z_лт, по оси y - Z_обн).

Построение графика РХ в общем виде в обычной системе координат нами уже производилось в 2.2.3 (см. рис.8). При построении РХ этим способом по экспериментальным данным достаточно нанести на поле графика две точки с координатами, полученными в 1 и 2 сериях (рис.13).

Для каждой экспериментальной точки определяются доверительные интервалы (при выбранной доверительной вероятности β) по осям P_обн и P_лт – на рисунке они представлены в виде горизонтальных и вертикальных отрезков, проходящих через экспериментальные точки. На практике построение такой PX применяется редко, так как не дает простого способа графического расчета d.

Гораздо чаще встречается построение PX в Z-координатах, которые также называются двойными нормальными координатами, поскольку построены исходя из предположения, что исходные величины подвергаются Z-преобразованию Фишера, опирающемуся на нормальный (гауссовский) закон распределения плотности вероятности. В используемом нами подходе предполагается, что распределения сенсорных эффектов f(s)и f(n) подчиняются именно нормальному закону распределения.

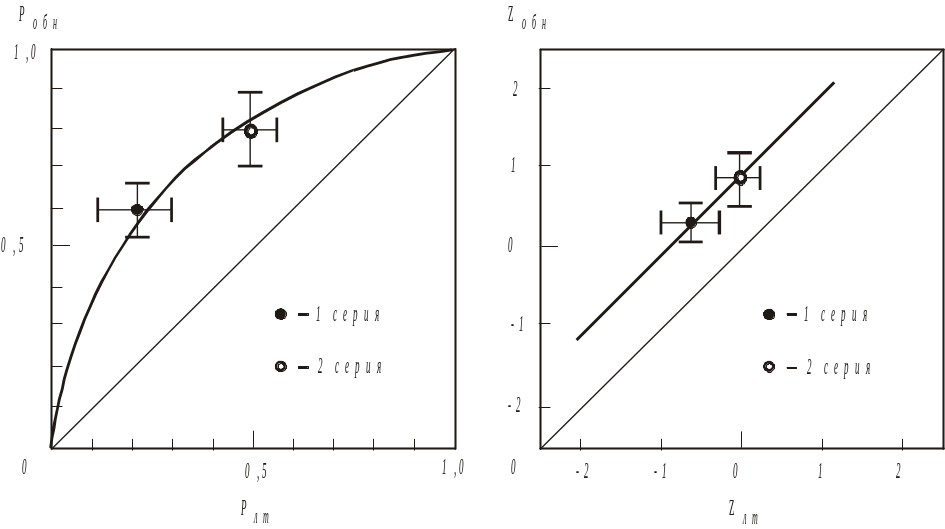
Рис.13. Рабочие характеристики наблюдателя в линейных (слева) и двойных нормальных (справа) координатах (β≤0,95)

Для того, чтобы построить PX в Z-координатах, надо перевести значения P_обн и P_лт в Z-единицы. Сделать это можно, используя специальные таблицы Z-преобразования, где даны рассчитанные значения интеграла нормального распределения, и которые приводятся в любом руководстве по теории вероятности и математической статистике.

Для нашего примера имеем: