1. Додавання двійкових чисел без знаків

Додавання в двійковій системі числення відбувається подібно до звичайного дода­вання в десятковій системі. Додаються два розряди, які розміщені у числі на одній по­зиції. При виникненні переносу він передається в старший розряд і там додається. В загальному додавання можна описати наступними формулами:

S. = х. XOR у. XOR с.

її У і і

C_x__x = (х. AND у) OR (х. AND с.) OR (у. AND с.)

^со = °

де: S. - і-тий розряд суми, х., у. - і-ті розряди першого та другого доданків відповідно, с. - розряд переносу.

Ці формули отримані з наступної таблиці істинності (табл. 6.5).

Таблиця 6.5

с. ... .1 ......	х. . • - t	If	S: т
0	0	0	0	0
0	0	1	І	0
0	1	0	І	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Якщо результат, який мав би бути отриманий після додавання, є більшим, ніж може вміститися в даній розрядній сітці, то старший розряд втрачається і така ситуація на­зивається втратою результату через переповнення.

Приклади виконання операції додавання двійкових чисел без знаків приведено на рис. 6.7.

11 11 10 110 0 11

110 10 110

¹0 1 1 0 1 ¹0 ¹1 1 0 1 0 0 0 0 0 1

+

+

1

1 0 0 0 1 0 0 1

0 10 110 0

Переповнення

Рис. 6.7. Приклади виконання операції додавання двійкових чисел без знаків

*

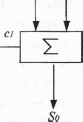
Позначимо оператор виконання операції однорозрядного двійкового додавання від­повідно до табл. 6.5 знаком суми, як це показано на рис. 6.8.

Хі уг

Т Бі

Рис. 6.8. Оператор однорозрядного двійкового додавання

Тут Б - і-й розряд суми, х, у. - і-ті розряди першого та другого доданків відповідно, с. та с - відповідно і-й та (і+1)-й розряди переносу. Тоді граф алгоритму п-розрядного додавання буде мати вигляд, показаний на рис. 6.9. Показаний на рис. 6.9. алгоритм на­зивається алгоритмом додавання двійкових чисел з послідовним переносом, оскільки перенос проходить через всі оператори однорозрядного двійкового додавання.

хо уо

	Хп-1 Л'п-1 1 1		Хп-2 уп-2 1 1		XI VI і 1
Сп ^	X	Сп-1		Сп-2 ^ ...	X

Рис. 6.9. Граф алгоритму п-розрядного додавання двійкових чисел з послідовним переносом

Сі

Вхідними даними тут є двійкові числа х_п1, х_{п 2}, ..., х₀ та у_{п 1?} у_п2, ..., у₀, а вихідним - двійкове число 5,5,..., Б , яке є сумою вхідних чисел. Показаний алгоритм додаван­ня є доволі простим. Недоліком представленого алгоритму є його суттєва часова склад­ність, тобто велика кількість операцій, які знаходяться на критичному шляху, оскільки

Сі+1

со

т

А

▼

▼

для отримання останнього розряду суми перенос повинен бути сформованим всіма опе­раторами однорозрядного двійкового додавання. Для зменшення кількості операцій, які знаходяться на критичнохму шляху, створено ряд алгоритмів додавання, в яких скороче­но кількість послідовних операцій при формуванні переносу. Це здійснюється шляхом паралельного формування переносів для всіх розрядів (так званий прискорений пере­нос), або паралельного формування переносів для груп розрядів (так званий частково- прискорений перенос), або використання алгоритму за методом вибору переносу.