Задача № 2
На основе исходных данных задачи № 1 и рассчитанных при решении задачи параметров линейного тренда:
Построить прогнозную полиноминальную адаптивную модель первого порядка.
Сделать по полученной модели прогнозные расчеты динамики прожиточного минимума в регионе с временем учреждения прогноза 4 месяца (по месяцам) и определить доверительные интервалы прогноза.
Порядок решения
1. Из решения задачи № 1 параметры линейного тренда: а =..., b =... . Прогнозный полином первого порядка имеет вид:
(2*)
где
параметры
уравнения, рассчитываемые на основе
экспоненциальных средних первого и
второго порядков.
Для расчета экспоненциальных средних определяется параметр сглаживания
и
параметр
Формула экспоненциальной средней любого порядка имеет следующий вид:
где R – порядок средней,
t – порядковый номер
уровня динамического ряда. При этом
Начальные условия задачи (
и
)
определяется на основе параметров
уравнения линейного тренда, рассчитанных
в задаче 1 по следующим соотношениям:
Экспоненциальная средняя первого порядка – (k=1) для первого уровня динамического ряда (t = 1) будет равна:
Экспоненциальная средняя второго порядка для первого уровня ряда:
=
Высчитываем последовательно все экспоненциальные средние всех уровней и заносим их в таблицу 2.1.
На базе экспоненциальных средних определяются параметры полинома первого порядка для всех уровней динамического ряда со сдвигом на один шаг вперед:
;
Например,
;
Выравненные значения будут равны:
Последние полученные на основе динамического ряда параметры, т.е. аn+1 и bn+1 и будут параметрами прогнозного полинома первого порядка.
Расчеты провести в следующей таблице:
Таблица 2.1
Построение модели прогнозного полинома первого порядка
№ п/п |
yt |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n+1 |
|
|
|
|
|
|
|
2. Прогнозные значения показателя рассчитываются но формуле (2*), подставляя в нее соответствующее время упреждения.
Доверительный интервал прогноза рассчитывается по формуле:
где
- прогнозное
значение показателя определенное по
прогнозному полиному на время упреждения
- ошибка прогноза на время упреждения
L
- ошибка прогноза на время упреждения
L
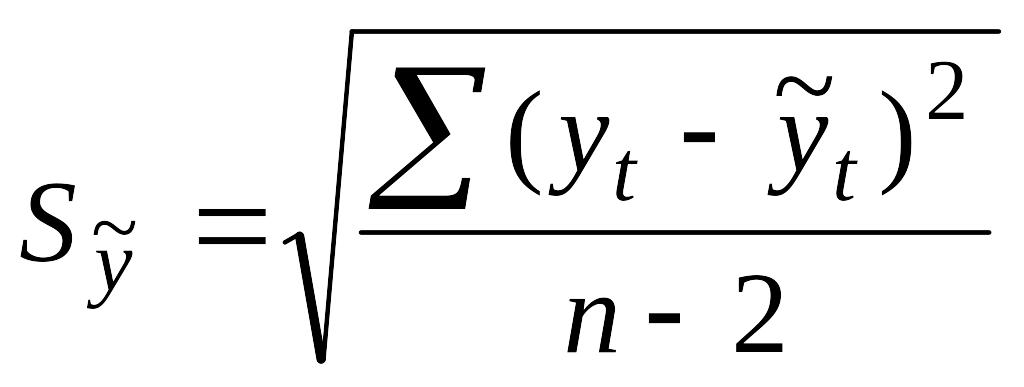
Расчеты представить в следующей таблице:
Таблица 2.2
Прогноз по прогнозному полиному первого порядка
Время упреждения (L) |
KL |
Ошибка прогноза (SpL) |
Прогноз |
||
нижняя граница |
средняя граница |
верхняя граница |
|||
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|