Прототип b13 № 99615

Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?

Решeние:

Обозначим объем бака за 1. Тогда три насоса, работая вместе, заполнят бак за

минут.

Ответ: 10.

Прототип b13 № 99614

Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?

Решeние:

Первый мастер выполняет 1/12 работы в час, а второй — 1/6 работы в час. Следовательно, работая вместе, мастера выполняют работы в час. Поэтому всю работу мастера выполнят за 4 часа. Другое рассуждение. Время работы равно отношению объёма к скорости её выполнения. Поэтому два мастера, работая вместе, выполнят заказ за

часа.

Ответ: 4.

Прототип b13 № 99613

Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Решeние:

Рабочий выполняет 1/15 часть заказа в час, поэтому за 3 часа он выполнит 1/5 часть заказа. После этого к нему присоединяется второй рабочий, и, работая вместе, два рабочих должны выполнить 4/5 заказа. Чтобы определить время совместной работы, разделим этот объём работы на совместную производительность:

часов.

Тем самым, на выполнение всего заказа потребуется 6 + 3 = 9 часов.

Ответ: 9.

Прототип b13 № 99596

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

Решeние:

Пусть км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна км/ч. Пусть первый раз мотоциклисты поравняются через часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому

.

Таким образом, мотоциклисты поравняются через  часа или через 20 минут.

Ответ: 20.

Прототип b13 № 26579

Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути – со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.

Решeние:

Пусть км/ч – скорость первого автомобиля, тогда скорость второго автомобиля на первой половине пути равна  км/ч. Примем расстояние между пунктами за 2. Автомобили были в пути одно и то же время, отсюда имеем:

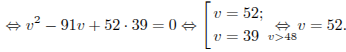
Таким образом, скорость первого автомобиля была равна 52 км/ч.

Ответ: 52.

Прототип b13 № 26590

От пристани A к пристани B отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 1 км/ч большей отправился второй. Расстояние между пристанями равно 420 км. Найдите скорость первого теплохода, если в пункт B оба теплохода прибыли одновременно. Ответ дайте в км/ч.

Решeние:

Пусть км/ч — скорость первого теплохода, тогда скорость второго теплохода по течению равна км/ч. Первый теплоход находился в пути на 1 час больше, чем второй, отсюда имеем:

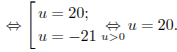
Таким образом, скорость первого теплохода равна 20 км/ч.

Ответ: 20.