
- •Минобринауки россии
- •Контрольная работа Предмет: Статистика
- •Задача №1
- •Решение
- •Задача №2 Вариант 2
- •Сравнительные данные по некоторым странам мира за 1995 год
- •Виды абсолютных величин:
- •Формы учета абсолютных величин:
- •Решение
- •Задача №3
- •Вариант 2
- •Абсолютные показатели вариации включают:
- •Среднее линейное отклонение простое:
- •Решение
- •Задача №4
- •Вариант 2
- •Решение
- •Задача №5
- •Вариант 2
- •Решение
- •Задача №6 Вариант 2
- •Статистика осуществляет классификацию индексов по следующим признакам:
- •Решение
Вариант 2
Динамика численности занятого населения в сфере жилищно-коммунального хозяйства и непроизводственных видов бытового обслуживания России характеризуется следующими показателями:
Годы |
Численность занятого населения, тыс. чел. |
1990 1991 1992 1993 1994 1995 |
4238 4305 4227 4243 4394 4500 |
Первый период: 1990-1992 гг.
Второй период: 1993-1995 гг.
Теория
Ряд, расположенных в хронологической последовательности значений статистических показателей, представляет собой временной (динамический) ряд.
Статистические показатели, характеризующие изучаемый объект, называют уровнями ряда.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на:
- моментные;
- интервальные.
Абсолютный
прирост (базисный) ![]() ,
где
,
где ![]() –
любой уровень,
–
любой уровень, ![]() –
первый уровень ряда.
–
первый уровень ряда.
Абсолютный
прирост (цепной) ![]() ,
где
–
любой уровень,
,
где
–
любой уровень, ![]() –
предшествующий уровень ряда.
–
предшествующий уровень ряда.
Средний
абсолютный прирост ![]() ,
где
–
первый уровень ряда,
,
где
–
первый уровень ряда,
![]() –
последний уровень ряда, n – количество
уровней.
–
последний уровень ряда, n – количество
уровней.
Коэффициент
роста (базисный) ![]() ,
где
–
любой уровень,
–
первый уровень.
,
где
–
любой уровень,
–
первый уровень.
Коэффициент
роста (цепной) ![]() ,
где
–
любой уровень,
–
предшествующий уровень ряда.
,
где
–
любой уровень,
–
предшествующий уровень ряда.
Темп
роста ![]() %.
%.
Темп
прироста ![]() %.
%.
Абсолютное
значение одного процента прироста![]() .
.
Средний уровень ряда динамики характеризует типичную величину абсолютных уровней.
Способы расчета зависят от вида динамических рядов.
Интервальный ряд.
а) при условии равных интервалов формула среднего уровня ряда находится по формуле простой средней арифметической:
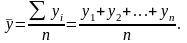
б) при условии неравных интервалов применяется формула средней арифметической взвешенной, весами служат промежутки времени

Моментный ряд
а) моментный ряд динамики с равностоящими датами времени
Средний уровень ряда определяется по формуле средней хронологической
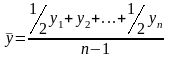
Формула для расчета среднего коэффициента роста для равностоящих рядов динамики:
 ,
,
где т — число уровней ряда динамики в изучаемом периоде, включая базисный.
Решение
Вид динамического ряда – интервальный.
Примем 1990 год за базисный.
Результаты расчетов базисных и цепных величин показаны в табл. 10
Таблица 10
Годы |
Числен-ность заня-того населе-ния, тыс. чел. |
Абсолютные приросты ∆y, тыс. чел.
|
Темпы роста Тр, % |
Темпы прироста Тпр, % |
Абсо-лютное значение 1% прироста Аi, тыс. чел. |
||||
Цеп-ные |
Базис-ные |
Цеп-ные |
Базис-ные |
Цеп-ные |
Базис-ные |
||||
1990 1991 1992 1993 1994 1995 |
4238 4305 4227 4243 4394 4500 |
- 67 -78 16 151 106 |
- 67 -11 5 156 262 |
- 101,6 98,2 100,4 103,6 102,4 |
100 101,6 99,7 100,1 103,7 106,2 |
- 1,6 -1,8 0,4 3,6 2,6 |
- 1,6 -0,3 0,1 3,7 6,2 |
- 41,88 43,33 40,00 41,94 40,77 |
|
Итого |
25907 |
- |
- |
- |
- |
- |
- |
- |
|
Примеры расчетов:
∆уцепной=4305-4238=67 тыс, чел.
∆убазисный=4227-4238=-78 тыс чел.
Тр цепной=4305/4238*100%=101,6%
Тр базисный=4227/4238*100%=99,7%
А= -78/-1,8=43,33 тыс. чел.
Остальные расчеты выполнены аналогично.
Рассчитаем среднегодовой темп роста:
Тср=(1,016*0,982*1,004*1,036*1,024)1/5**100%=(1,062)1/5*100%=101,2%
Результаты расчетов по двум периодам представлены в табл. 11
Таблица 11
Первый период 1990-1992 гг. |
Второй период 1993-1995 гг. |
||||||
уср, тыс. чел. |
∆уср, тыс. чел. |
Тр, % |
Тпр, % |
уср, тыс. чел. |
∆уср, тыс. чел. |
Тр, % |
Тпр, % |
4256,7 |
-5,5 |
99,9 |
-0,1 |
4379,0 |
128,5 |
103,0 |
3,0 |
По данным таблицы видно, что численность занятого населения в первом периоде падала, так как темп прироста отрицательный, а во втором периоде выросла на 3%.
