Задача №3

Для каждого варианта задачи №3 рассчитайте среднюю арифметическую и структурные средние (моду и медиану) вариационных рядов. Проанализируйте степень колеблемости признака с помощью всех показателей вариации. Сделайте выводы об однородности совокупности и типиности средней арифметической.

Используя исходные данные своих вариантов представьте интервальные вариационные ряды в виде гистограммы, полигона и кумуляты.

Вариант 2

Таблица 8

Среднедушевой размер общей площади, кв. км.	Число домохозяйств в процентах к итогу
До 5,0 5,0-7,0 7,0-9,0 9,0-13,0 13,0-15,0 15,0-20,0 20,0 и более	1,0 2,5 5,3 19,6 13,3 24,4 33,9
Итого	100,0

Теория

Вариацией называется различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени.

Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.

Абсолютные показатели вариации включают:

• размах вариации 

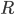
• среднее линейное отклонение 

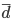
• дисперсию 

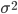
• среднее квадратическое отклонение 

Размах вариации — это разность между максимальным и минимальным значениями признака

Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.

Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность  .

При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю  , либо возводить значения отклонений в квадрат 

Среднее линейное отклонение   — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.

Среднее линейное отклонение простое:

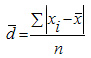
Среднее линейное отклонение взвешенное применяется для сгруппированных данных:

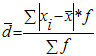
Наиболее совершенной характеристикой вариации является среднее квадратическое отклонение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение ( ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Среднее квадратическое отклонение простое:

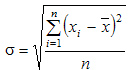
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:

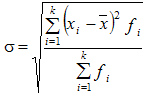
Дисперсия  - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия простая:

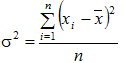
Дисперсия взвешенная:

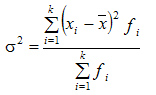
Более удобно вычислять дисперсию по формуле:

которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.

Для несгрупиированных данных:

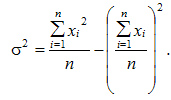
Для сгруппированных данных:

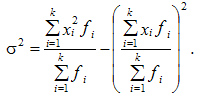
Частоты вариационного ряда – это абсолютная численность отдельных групп с различными значениями признака.

Частости вариационного ряда – удельные веса (доли) отдельных групп в общей численности совокупности.

Гистограмма – столбиковая диаграмма, для построения которой на оси абсцисс откладываются отрезки, равные величине интервалов вариационного ряда. На отрезках строят прямоугольники, высота которых в принятом масштабе соответствует частотам (или частостям).

Гистограмма легко может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить отрезками прямых, при этом середины верхних сторон двух крайних прямоугольников соединить с осью абсцисс в точках, отстоящих в принятом масштабе на величину интервалов от середины первого и последнего интервалов.

Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости.

Простая средняя арифметическая — Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности

Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

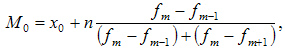
где:  — значение моды,  — нижняя граница модального интервала,  — величина интервала,  — частота модального интервала,  — частота интервала, предшествующего модальному,  — частота интервала, следующего за модальным.

Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части. При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

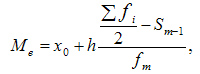
где:  — искомая медиана,  — нижняя граница интервала, который содержит медиану,  — величина интервала,  — сумма частот или число членов ряда,  - сумма накопленных частот интервалов, предшествующих медианному,  — частота медианного интервала.

Расчет модального и медиального значений для вариационных рядов с неравными интервалами осуществляется по формулам, аналогичным выше, только вместо показателей частот (частостей) используются показатели плотности распределения (находятся как отношение частот (частостей) к величине интервала).