3.1 Помехоустойчивые коды

Это коды, способные обеспечивать обнаружение и определение места одной и более одной ошибок в кодовых комбинациях. Для понимания механизма обнаружения ошибок можно рассмотреть геометрическую интерпретацию -разрядного кода, например, . Вершины куба, представленного на рисунке 3.1, есть кодовые комбинации. Переход от одной комбинации к другой – это переход от одной вершины куба к другой.

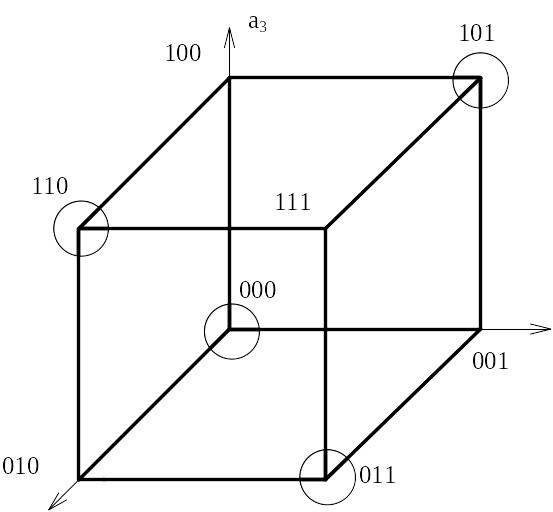
Рисунок 3.1

Некоторые основные определения. Кодовое расстояние – минимальное число граней, которое нужно пройти от одной вершины к другой. Вес кодовой комбинации (по Хэммингу) – число единиц в кодовой комбинации. Кодовое расстояние (КР) определяет число разрядов, отличных у двух рассматриваемых кодовых комбинаций, и алгебраически может быть найдено путем их поразрядного сложения. Вес суммы и даст значение КР для этих комбинаций. Минимальное кодовое расстояние – минимальное КР из всех для рассматриваемого кода. То есть если КР определяется только для двух комбинаций, то минимальное КР – это уже характеристика всего кода.

Отсюда можно сделать вывод, что для избыточных кодов . Если строго , то при изменении одного разряда будет получена неиспользуемая (запрещенная) кодовая комбинация. Помехоустойчивый код – это код с . На рисунке 3.1 представлен 3-разрядный код. Если из использовать только четыре отмеченных кружками, то получим код с , что хорошо видно. Это код с проверкой на четность – простейший помехоустойчивый код. Значение любого его разряда равно сумме по модулю 2 всех остальных. Если изменить один разряд (или нечетное число разрядов), то это правило будет нарушено. Действительно, новая комбинация будет из множества запрещенных.

Если – число возможных ошибок, то

(3.2)

для обнаружения без исправления t ошибок и

.

(3.3)

для обнаружения и исправления t ошибок.

Обобщенное требование будет иметь вид:

,

(3.4)

где – число обнаруживаемых ошибок;

– число исправляемых ошибок.

Очевидно, что должно быть . Из всего следует:

• кодовая комбинация (далее вектор кода или просто вектор) с числом ошибок меньше коду не принадлежит и наоборот;

• из (3.2) – два разных вектора кода при появлении в них до ошибок могут дать одинаковый вектор из числа запрещенных, что и не позволяет различить эти ошибки;

• для различения ошибок каждому вектору кода для каждого варианта размещения ошибок должен соответствовать только один запрещенный вектор, что и позволяет определить место ошибки. Это условие обеспечивается выполнением (3.3) или (3.4).

Можно сказать, что помехоустойчивость обеспечивается информационной избыточностью таких кодов.

3.2 Построение кодов Хэмминга (кодирование)

Коды Хэмминга являются наиболее используемыми и, в то же время, самыми наглядными помехоустойчивыми кодами. Относятся к числу разделимых кодов, то есть таких, у которых информационные разряды и избыточные (контрольные) разделяются.

Для любого помехоустойчивого кода первой задачей является определение минимально необходимого числа проверочных разрядов . Задавшись числом исправляемых ошибок , число контрольных разрядов можно определить из неравенства:

,

(3.5)

где – общая разрядность кода, ;

- число сочетаний из по .

Эта оценка не связывает прямо с и может оказаться завышенной, что нежелательно, так как это ведет к увеличению общей разрядности кода. Но в процессе построения самого кода можно будет уточнить величину .

Коды Хэмминга представляют собой пример так называемых линейных групповых кодов (ЛГК), которые полностью описываются математически. ЛГК – конечная группа двоичных векторов разрядностью , для которой определена операция суммирования по . ЛГК может быть задан перечислением этих векторов, либо матричным представлением, в которой из всей группы будут представлены только линейно-независимые вектора. Матрица, содержащая все такие вектора ЛГК, называется порождающей:

,

(3.6)

где каждая строка есть вектор ЛГК.

Таким способом может быть задан обычный натуральный не избыточный код, например, для . В этом случае , то есть :

,

(3.6)

откуда могут быть получены все вектора кода ( - суммирование по ):

строка 1 – 1 0 0; строка 2 – 0 1 0; строка 3 – 0 0 1;

строки 12 – 1 1 0; строки 13 – 1 0 1; строки 23 – 0 1 1;

строки 123 – 1 1 1; единичный элемент ЛГК – 0 0 0.

То есть получены все 8 комбинаций кода разрядностью .

Для кодов Хэмминга порождающая матрица будет иметь вид:

,

(3.7)

или

,

где – единичная матрица информационных разрядов;

– матрица проверочных разрядов.

Введем обозначения:

- , – исходный натуральный код;

- – вектор натурального кода размерностью .

;

- . – ЛГК;

– вектор ЛГК размерностью .

;

.

Тогда правило кодирования будет иметь вид:

,

(3.8)

где - умножение вектора на матрицу.

В результате будут получены элементы вектора :

; ; … ;

;

;

…

.

Выражения для , ,…, есть выражения для определения значений контрольных разрядов, то есть логическое задание кодера кода Хэмминга. Остается задать подматрицу , число столбцов которой равно числу вводимых проверочных разрядов.

Для построения прежде задается число исправляемых ошибок . Из этого определяется величина и по (3.5) число проверочных разрядов . Каждый их столбцов подматрицы получают как результат линейной комбинации 2-х, 3-х и так далее до столбцов матрицы . Если велико и таких комбинаций недостаточно, то остальные столбцы подматрицы получают путем линейной комбинации уже полученных столбцов . При этом анализируются:

• вектора-строки матрицы – каждая строка должна иметь вес ;

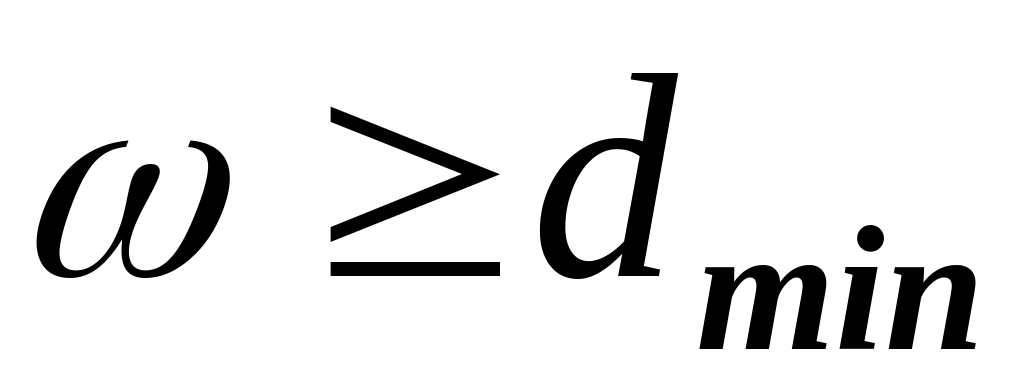• вектора-столбцы (проверочные вектора) , полученные из – вес каждого должен быть ;

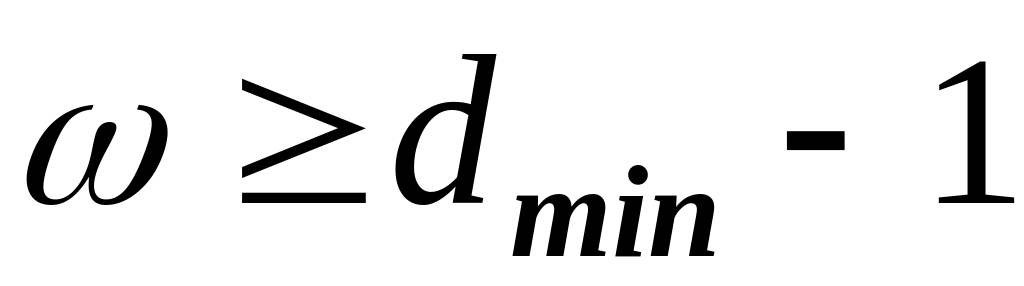• вектора-столбцы (проверочные вектора) , полученные из – вес каждого должен быть ;

• попарно все строки – для каждой пары КР должно быть ;

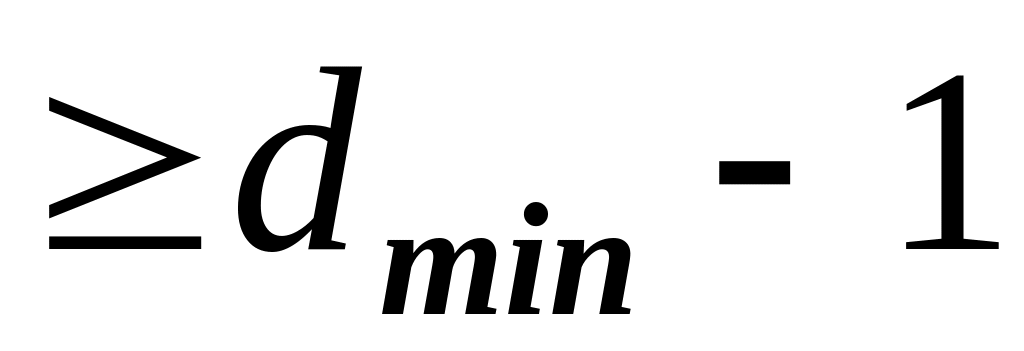• попарно все столбцы – для каждой пары КР должно быть .

По достижении требуемых условий проверяются все остальные вектора кода, получаемые как линейные комбинации строк матрицы – каждый из них также должен иметь вес . Наконец, минимальный вес вектора из всех векторов кода даст значение истинного , то есть это является проверкой правильности формирования образующей матрицы.

Замечание: при больших и можно построить много вариантов подматрицы . Из всех следует брать прежде всего тот, который содержит в как можно меньше единиц, так как каждая единица – это одна операция  в (3.8).
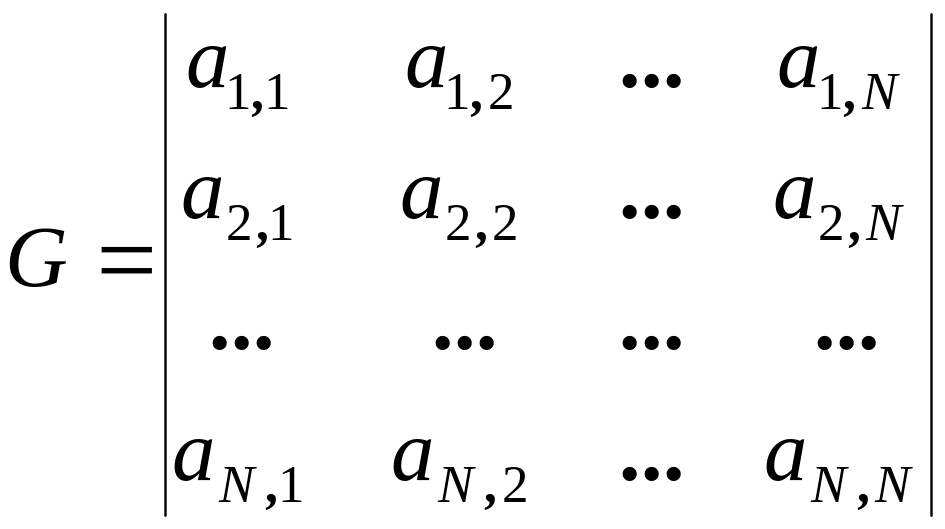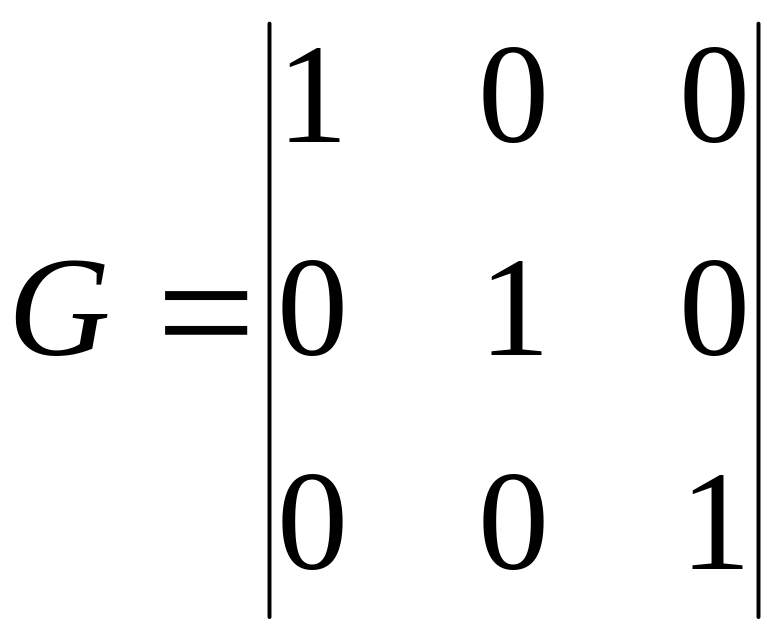