1 Цель работы Целью работы является изучение основных характеристик случайных процессов по их реализациям на конечном интервале времени.

2. Задачи работы

Основными задачами работы являются:

1. Изучение харктеристик случайных процессов на примере шумоподобных сигналов, получаемых с использованием генераторов псевдослучайных чисел.

2. Изучение способов получения псевдослучайных сигналов алгоритмическими и аппаратными способами.

3. Краткие теоретические сведения

Физические явления, рассматриваемые в инженерных задачах, описываются, как правило, функциями времени, называемыми реализациями процесса. Физические явления, будущее поведение которых с вполне приемлемой точностью может быть предсказано на основе физических соображений, называют детерминированными. Однако многие явления, которые имеют место в различных устройствах и системах, недетерминированы. Каждая серия измерений дает свою реализацию процесса, которая с малой вероятностью повторится в будущем и которую невозможно предсказать с необходимой точностью. Эти процессы и порождающие их физические явления называются случайными.

3.1 Характеристики случайных процессов

Случайные процессы описываются статистическими характеристиками. Из определения случайного процесса следует, что случайный процесс или описывающая его случайная функция есть переменная во времени случайная величина. Следовательно, возможными значениями случайного процесса – его реализациями являются функции времени , ,…, .

Рассматривая множество таких реализаций, можно получить следующие основные характеристики.

Одномерная функция распределения. Реализации исследуемого процесса рассматриваются в выбранный момент , строится вероятностная функция:

,

(2.1)

где меняется в диапазоне .

Таким образом, для каждого сечения получим распределение вероятности. На рисунке 2.1 представлены функции распределения для случайного и детерминированного процессов.

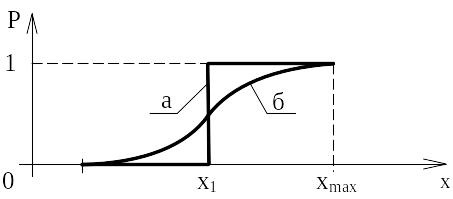
а - детерминированный процесс, ;

б - случайный процесс

Рисунок 2.1 – Функции распределения

Одномерная плотность вероятности случайного процесса. Определяется также для конкретного временного сечения на множестве реализаций в случае, если функция распределения имеет частную производную:

.

(2.2)

На рисунке 2.2 представлены одномерные плотности распределения для случайного и детерминированного процессов. Можно видеть, что две эти функции характеризуют случайный процесс только в отдельных сечениях и не определяют связь между этими сечениями.

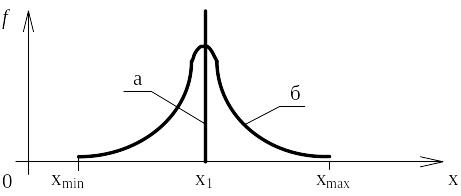
а - детерминированный процесс, x(t₁) = x₁;

б - случайный процесс

Рисунок 2.2 – Плотность функции распределения

Более полную характеристику случайных процессов дают многомерные функции распределения и их плотности, которые связывают более одного сечения по времени:

,	(2.3)
.	(2.4)

Рассмотренные функции определяют характер распределения процесса по сечениям. Следующие характеристики дают информацию об усредненном значении и степени разбросанности по каждому сечению.

Математическое ожидание случайного процесса является функцией времени и для каждого сечения определяется как среднее на множестве реализаций:

.

(2.5)

Дисперсия случайного процесса также является функцией времени и характеризует разброс (максимальное отклонение) значения процесса для конкретного сечения:

.

(2.6)

Необходимо отметить, что и не характеризуют взаимосвязь между сечениями процесса и могут принимать одни и те же значения для различных по изменению во времени случайных процессов.

Наиболее полно взаимосвязь между произвольными сечениями характеризуют корреляционные функции (КФ). В простейшем случае для одного процесса по его реализациям определяют автокорреляционную функцию (АКФ), связывающую два произвольных сечения и :

.

(2.7)

где – двумерная плотность вероятности случайного процесса .

Если положить , то получится выражение (2.6) для дисперсии случайного процесса. Рассматривая более двух сечений, получают КФ порядка более второго, которые и характеризуют связь между этими сечениями.

Наконец, можно рассмотреть два разных процесса и определить для них плотность вероятности двух процессов по двум произвольным сечениям :

.

(2.8)

Подставляя в (2.7) вместо и соответственно и двух разных процессов и (2.8), получают выражение для определения степени взаимосвязи двух процессов по двум произвольным сечениям, называемое взаимной КФ.

Использование характеристик (2.1) … (2.8) крайне неудобно из-за необходимости получать достаточно большое число реализаций случайного процесса, что иногда бывает просто невозможно. Рассмотренные характеристики являются наиболее общими и используются в случаях, когда характер случайных процессов дополнительно не определен по типам, классификационным признакам.

В то же время, анализируя процессы, можно выделить ряд важных признаков и свойств, позволяющих работать с более удобными по форме характеристиками. Среди наиболее важных свойств следует выделить свойство стационарности. Случайный процесс обладает свойством стационарности, если его математическое ожидание есть величина постоянная, а КФ зависит только от разности аргументов:

.

(2.9)

В этом случае дисперсия случайного процесса будет определяться значением КФ при . Также КФ стационарных случайных процессов сохраняют свойство четности. Действительно, в (2.7) изменение порядка следования и не меняет общего результата, следовательно, по (2.9) будет выполняться:

.

(2.10)

Аналогично для двух стационарных процессов определяется взаимная КФ, зависящая только от разности аргументов и сохраняющая свойство четности. Другим важным свойством, которым могут обладать случайные процессы, является свойство эргодичности. Стационарный процесс является эргодическим, если любая статистическая характеристика, определяемая на множестве реализаций, с вероятностью, близкой к единице, равна соответствующей характеристике, определяемой усреднением по времени любой, достаточно продолжительной реализации этого процесса.

Свойство эргодичности очень важно, поскольку позволяет усредненные на множестве реализаций характеристики приравнивать к характеристикам, усредненным во времени по одной реализации. Это существенно упрощает процедуру анализа случайных процессов. В этом случае рассмотренные характеристики для стационарных и эргодических процессов будут иметь вид:

,	(2.11)
,	(2.12)
.	(2.13)

где – длительность реализации случайного процесса.

Необходимо отметить, что эргодичность не обусловлена стационарностью процесса. Строго математически свойство эргодичности для стационарного процесса проявляется при условии неограниченного убывания модуля АКФ при :

при .

(2.14)

где - сколь угодно малое положительное число;

– сколь угодно большое положительное число.

Типичный вид АКФ случайного стационарного эргодического процесса представлен на рисунке 2.3.

K_x

D_x



0 _инт 

Рисунок 2.3 – Корреляционная функция случайного