1.2Анализ функционирования системы массового обслуживания

Полагая, что покупатели прибывают в магазин «случайно» можно считать, что вероятность прибытия покупателя за любой малый промежуток времени [t, t+], начинающийся в произвольный момент времени t и имеющий продолжительность  с точностью до пренебрежимо малых величин пропорционально величине  c некоторым коэффициентом ⁵>0. Вероятность того, что за этот промежуток времени в магазин не прибудет ни одного покупателя может быть приблизительно оценена как 1-.

Исходя из этого, в теории вероятностей делаются выводы:

• промежутки времени  между двумя приходами покупателей подчиняются экспоненциальному распределению

_(t) = *exp(-*), t  0

• вероятность того, что за любой промежуток времени Т в магазин прибудет k покупателей (клиентов, заявок…) может быть определена как

т.е входной поток покупателей является пуассоновским.

 - интенсивность входного потока, т.е. среднее число заявок, поступающих в СМО в единицу времени.

 = 1/ [чел/мин; руб/час; чеков/час; кг/час…]

где  - среднее значение интервала времени между двумя соседними заявками (приходами покупателей).

• Случайное время ожидания в очереди начала обслуживания тоже можно считать распределенным экспоненциально.

f(t) = *exp(-t_оч)

где  - интенсивность движения очереди( среднее число заявок, поступающих на обслуживание в единицу времени;

 = 1/t_оч . t_оч - среднее значение времени ожидания в очереди.

• Выходной поток заявок (заявок, прошедших обслуживание) связан с потоком обслуживания в канале СМО также, в большинстве случаев, подчиняется показательному закону распределения с плотностью

F(t_обсл) = *exp(-t_обсл) ( 1‑0)

где  - интенсивность обслуживания в канале (одним продавцом…), т.е. среднее число заявок (клиентов), обслуживаемых в единицу времени.

 = 1/t_обсл = [ чел/мин; руб./день; кг./час; докум./день….]

• Одной из наиболее важных характеристик СМО, связывающей показатели  и , является интенсивность нагрузки (),

 = /, ( 1‑0)

которая показывает степень согласованности входного потока заявок с интенсивностью их обслуживания.

Величину  часто называют приведенной плотностью потока требования (заявок) или интенсивностью нагрузки - среднее число требований, приходящихся на среднее время обслуживания одного требования.

Важно заметить, что параметр  характеризует степень согласованности входного потока ( например, покупателей в магазине) с интенсивностью потока обслуживания. Процесс обслуживания будет стабилен при  < n. Если же   n, то в системе будет возрастать средняя длина очереди и среднее время ожидания покупателей начала обслуживания, и, следовательно, проектируемая СМО будет работать неустойчиво.

Рассмотрим наиболее общий случай СМО, когда n – канальная система работает в режиме с ожиданием обслуживания и с ограничением на длину очереди (в очереди не может быть более m требований). При этом, мы предполагаем, что входящий поток требований на обслуживание описывается пуассоновским законом распределения с интенсивностью , а время обслуживания требований распределено по показательному закону с интенсивностью .

• Вероятность того, что в системе отсутствуют требования (Р₀) может быть определена по формуле:

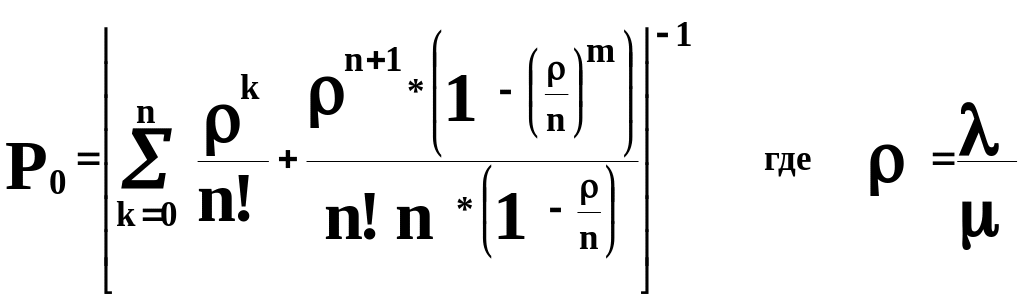
( 1‑0)

• Вероятность того, что в системе обслуживания находятся k требований на обслуживание (P_k) может быть определена как:

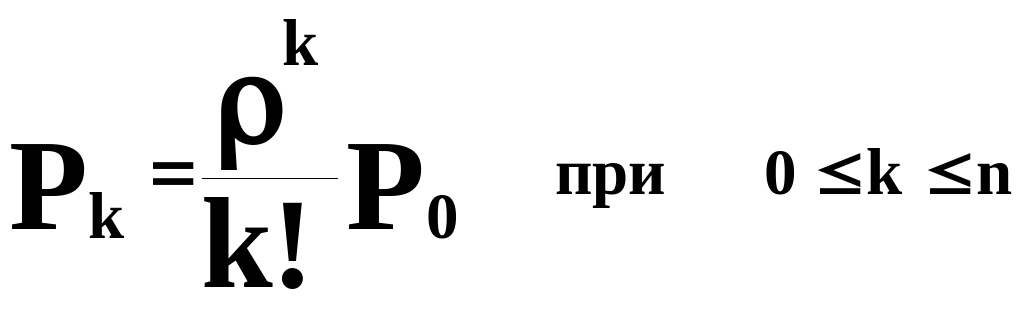( 1‑0)

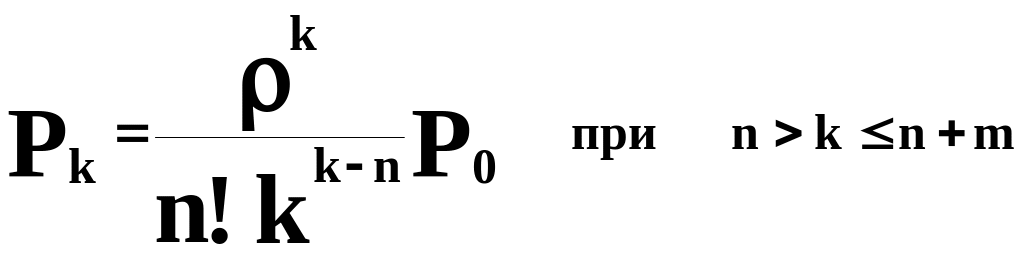( 1‑0)

Отношение /n часто обозначается через Х и называется уровнем загрузки системы.

Х = /n ( 1‑0)

Если Х = /n <1, то очередь на обслуживание не образуется и система находится в стационарном состоянии, которое характеризуется тем, что вероятность поступления определенного количества требований в течении заданного промежутка времени зависит только от его продолжительности.

• Вероятность отказа в обслуживании требования (заявки, клиента…), если в систему поступает n+m⁶ заявок на обслуживание

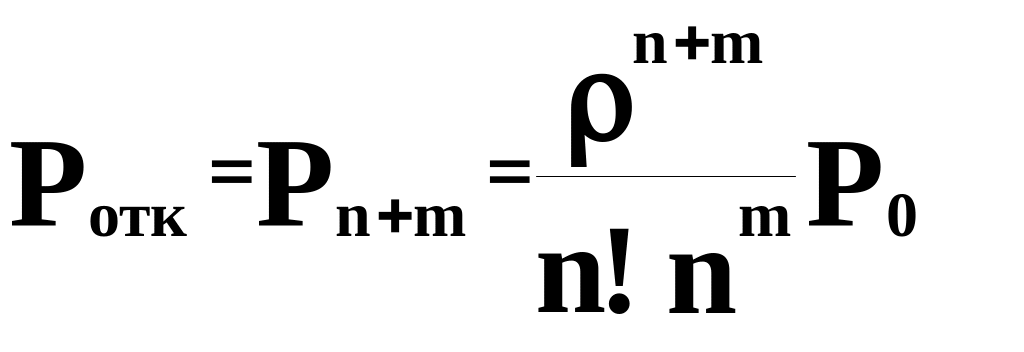( 1‑0)

• Вероятность обслуживания поступившей заявки (или относительная пропускная способность СМО)

P_обсл=1- Р_отк. ( 1‑0)

Абсолютная пропускная способность системы (число фактически обслуженных требований в единицу времени)

А=*Р_обсл. ( 1‑0)

среднее число занятых каналов⁷ обслуживания

( 1‑0)

так как А – это интенсивность потока обслуживания заявок, а каждый канал способен в единицу (в среднем) обслуживать  заявок.

• Коэффициент использования (занятости) каналов

К_зан = Х*Р_обсл = z_ср/n ( 1‑0)

• Коэффициент простоя каналов обслуживания

К_прос=т = 1-К_зан = 1-N_ср/n = 1-X*P_обсл. ( 1‑0)

• Среднее число требований (заявок) в очереди

L_ср =1*P_n+1+2*P_n+2+…m*P_n+m =

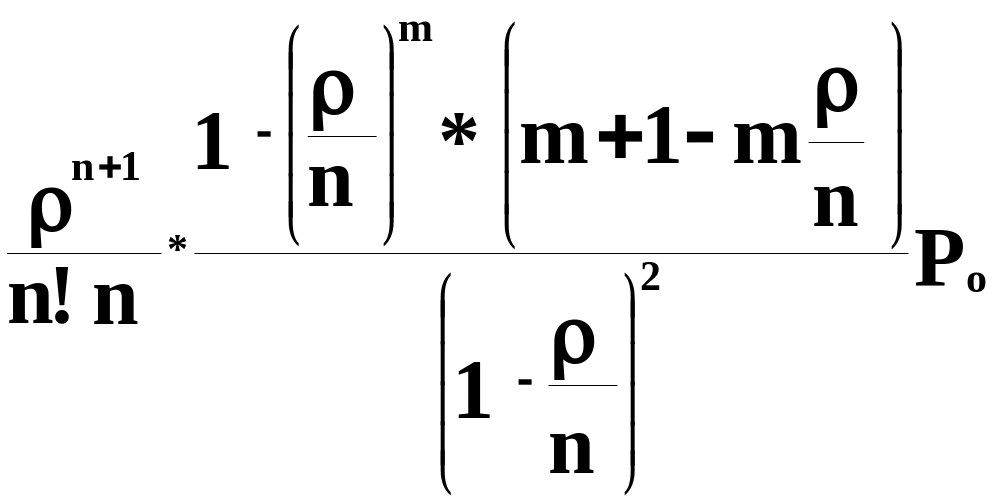( 1‑0)

• Среднее время обслуживания требований

Т_{ср(обсл)} = Р_обсл/ ( 1‑0)

• Среднее время ожидания в очереди

T_{ср(ож. оч)}= (1/n)P_n+(2/n)P_n+1…+(m/n)P_n+m+1 =

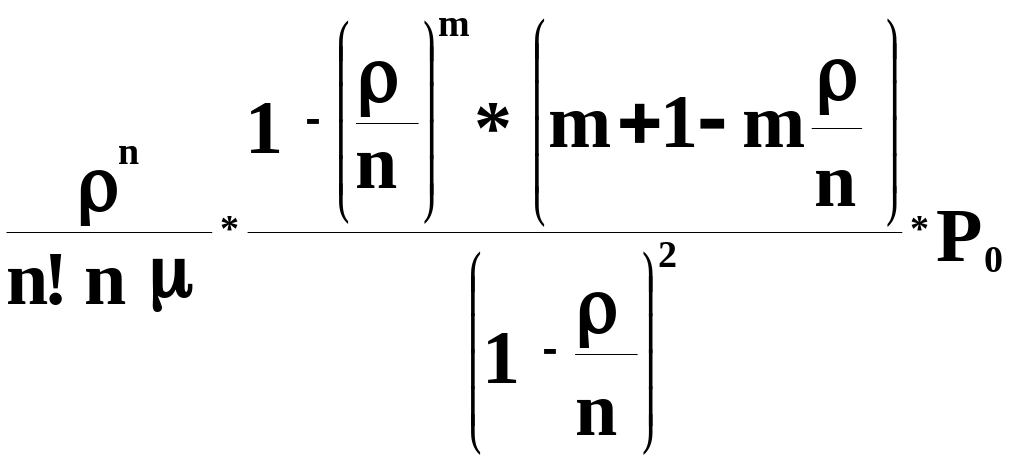
( 1‑0)

Так как, если заявка на обслуживание поступит в тот момент, когда все каналы заняты и очереди нет, то время ожидания составит в среднем 1/n, а если заявка поступит в тот момент, когда в очереди находится одно требование на обслуживание, 2/n и т.д.

• Среднее время пребывания заявки в СМО

Т _{ср. СМО} = T_{ср(ож. оч)} + t_{ср(обсл} ( 1‑0)

₎ Образование очереди возможно только тогда, когда вновь поступившая заявка застанет на обработке в системе не менее n требований на обслуживание⁸, т.е когда в СМО будет находиться n, n+1, n+2,…n+m-1 требований на обслуживание. Учитывая то, что заявки в СМО поступают независмо друг от друга, вероятность того, что все каналы обслуживания будут заняты равна сумме вероятностей Р_n, P_n+1, P_n+2,…P_n+m-1.

Отсюда вероятность образования очереди:

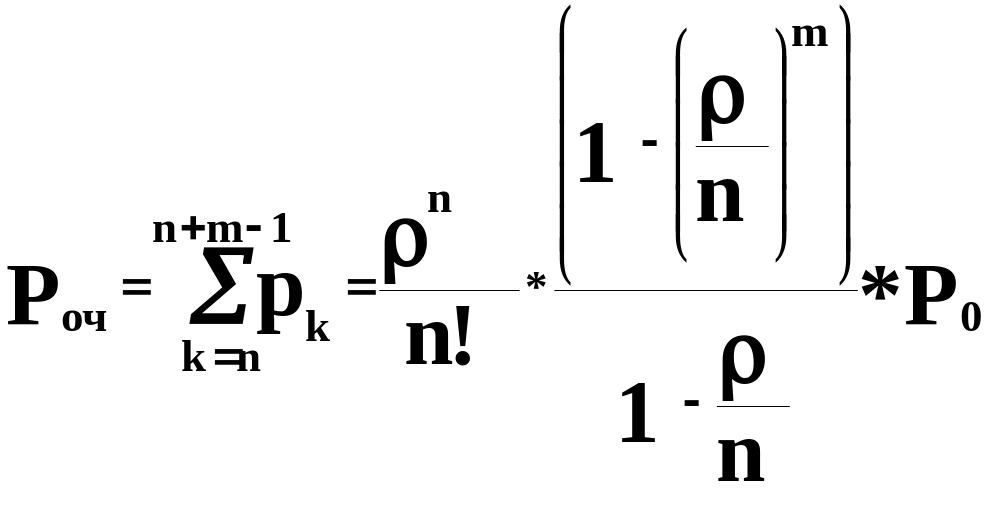
( 1‑0)

Выше были приведены формулы для расчета основных характеристик СМО для случая, в котором допускается возникновение очереди при наличии ограничения на ее длину⁹.

Если m=0, то мы имеем дело с первым частным случаем СМО – системы с отказами. Наиболее типичным примером такой СМО является работа стола заказов (или справочной службы) по телефону – если все телефоны заняты приемом заказов, то звонок нового покупателя получает отказ – сигнал занято.

В том случае, когда m  ¹⁰ , то получаем СМО с ожиданием без ограничения на длину очереди