6.Программная реализация конечного автомата
Программа, моделирующая работу конечного автомата, обеспечивает различение допускаемых и не допускаемых цепочек. Цепочки символов вводятся с клавиатуры компьютера, программа различения цепочек имеет как автоматический, так и пошаговый режим работы и отражает на экране монитора изменение состояний автомата в процессе различения цепочек. При переходе автомата в заключительное состояние (последовательность входных символов образует допустимую цепочку) и появлении признака конца цепочки программа формирует сигнал различения цепочки. При наличии цепочек, не принадлежащих языку полученной грамматики, программа формирует сигнал ошибки и указывает последнее из состояний автомата, в котором он находился до появления ошибочного символа.
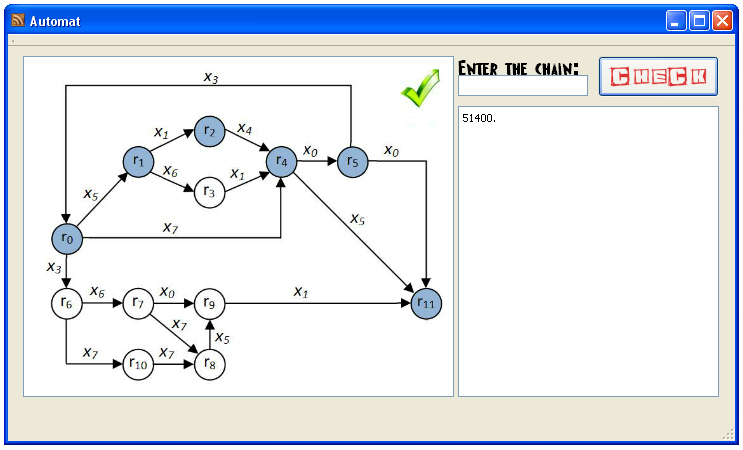
Рис.6. Пример распознанной цепочки
Рис.7. Пример нераспознанной цепочки
7.Использование сетей петри при переходе от грамматики к минимальному автомату
Для построения сети Петри рассмотрим полученную во втором пункте курсовой работы праволинейную грамматику G”. Это можно сделать, если поставить в соответствие нетерминальным символам места в сети, а терминальным символам – переходы сети. Обозначим места кружками, а переходы – прямоугольниками (полочками). Будем помечать места и переходы соответствующими терминальными и нетерминальными символами. Поскольку сеть Петри – двудольный граф, соединение дугами мест разрешается только через переходы, а переходов - через места.
Если в правой части
некоторого правила вывода из R
имеет место катенация терминалов, то в
сети Петри между переходами, помеченными
терминалами, появляются дополнительные
позиции. Эти позиции помечаются символами
левой части правила вывода с верхними
индексами 1,2,…. Поэтому фрагмент сети
Петри, соответствующий первому правилу
вывода (S
x5,x1,x4,A),
будет иметь следующий вид (рис.8).
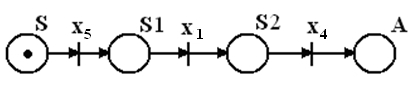
Рис.8
При построении остальных фрагментов сети Петри, соответствующих последующим правилам вывода, можно использовать ранее обозначенные места, но не переходы. Таким образом, места могут иметь по несколько входящих и исходящих дуг, но переходы – только по одной входящей и не более одной исходящей дуги (исходящей дуги может не быть, если в правой части правила вывода отсутствует замыкающий нетерминал).
Построим по полученным правилам вывода R’ сеть Петри (рис.9).
Рис.9
Построенная сеть представляет собой автоматную сеть Петри, и места можно трактовать как состояния конечного автомата, а переходы – как входные символы. Чтобы обеспечить полное соответствие построенной сети Петри автомату Мура, необходимо ввести не показанную на рис.9 заключительную позицию Z, в которую можно направить дуги из переходов, не имеющих исходящих дуг.
Если теперь рассмотреть отдельные фрагменты сети на рис.9, то нетрудно заметить одинаковые фрагменты: места А,В,С с одинаковыми инцидентными им переходами x0 и x5, а также еще два идентичных фрагмента с местами D и Е, каждому из которых инцидентны по два выходных перехода x3 и x0. Аналогично можно отметить места F1 и F7, F2 и F5, а также F3, F6 и F8. В то же время места S1 и S3 идентичны по входу, т.е. из места S в места S1 и S3 дуги идут через переходы x5.
Функционирование сети не изменится, если «склеить» идентичные фрагменты, что будет соответствовать минимизации числа состояний автомата. Источником недетерминированности могут быть места, из которых исходят дуги, являющиеся входящими дугами переходов, помеченных одинаковыми терминалами. В данном случае таким местом является начальное состояние S и переходы x5. Таким образом, производится устранение недетерминированности. В результате получим сеть Петри с минимальным числом мест (рис.10).
Можно также установить взаимно-однозначное соответствие между сетью на рис.10 и исходным орграфом.
Для этого местам сети ставятся в соответствие состояния автомата, а переходам – пометки на дугах.
Рис.10