4.Преобразование недетерминированного конечного автомата в детерминированный

Детерминированный конечный автомат это пятерка А=(Q,V,М,S,Z), где Q - алфавит состояний; V - входной алфавит; М - функция переходов (Q*VР(Q)); S - начальное состояние; Z - множество заключительных состояний; SZ.

В этом автомате, в отличие от недетерминированного, всегда одно начальное состояние, а также отсутствуют альтернативные состояния, в которые переходит автомат при подаче на вход одного и того же входного символа.

В рассматриваемом примере такими состояниями являются q₁ и q₃, в которые переходит автомат из состояния q_o под воздействием х₅.

Преобразование недетерминированного конечного автомата в детерминированный основано на замене альтернативных состояний одним, эквивалентным этим состояниям, например:

Здесь три альтернативных состояния X,Y,Z в недетерминированном конечном автомате представляются одним [XYZ] в детерминированном, которое представляет первые три состояния. Следовательно, если недетерминированный конечный автомат представляют пятеркой А=(Q,V_T,M,S,Z), то эквивалентный детерминированный конечный автомат имеет вид А=(Q,V_T,М',S,Z).

Алфавит состояний Q' определяется через подмножество алфавита Q.

Функция переходов М определяется как M([q₁,q₂,…,q_k],T)= [R₁,R₂,…,R_t], если в недетерминированном конечном автомате M({q₁,q₂,...,q_k},T) = {R₁,R₂,...,R_t}.

Начальное состояние S'=[S₁,S₂,...,S_i]=q_0, еcли S={S₁,S₂,...,S_i}.

Множество заключительных состояний Z' образуется из элементов, в которых присутствует хотя бы одно состояние из множества Z недетерминированного конечного автомата.

Построенный по этим правилам эквивалентный детерминированный конечный автомат допускает одни и те же входные цепочки, что и исходный недетерминированный.

Рис.2

В рассматриваемом примере недетерминированность автомата локально проявляется в том, что из некоторого его состояния q_i исходят несколько дуг, помеченных одним и тем же символом х_j (рис.2).

Недетерминированность в этом случае может быть легко устранена «склеиванием» двух состояний q₁ и q_k в одно q_1,k . При этом q_{1, k} инцидентны все исходящие дуги х_г, х_р, x_t, являющиеся исходящими дугами состояний q₁ и q_k (рис.3).

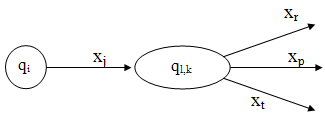
Рис.3

Общий алгоритм нахождения детерминированного конечного автомата, эквивалентного недетерминированному, может быть описан следующим образом:

1. Построить начальное состояние S' и отметить им первую строку таблицы переходов.

2. Определить все состояния Q', которые могут быть достигнуты из данного состояния.

3. Если во вновь определенных состояниях не встречаются такие, которые отмечали ранее строки таблицы, то для них надо выделить новые строки и повторить п.2.

4. В таблице переходов выделить заключительные состояния Z'.

Таблица 5

	X0	X1	X2	X3	X4	X5	X6	X7
q0				q10		q1,3		q7
q1,3		q2					q4
q2					q5
q4		q6
q5	q8					q19
q6	q9					q19
q7	q9					q19
q8	q19			q0
q9	q19			q0
q10							q11,17	q14
q11,17	q18							q12
q12						q13
q13		q19
q14								q15
q15						q16
q16		q19
q18		q19
q19

В результате применения этого алгоритма от автомата, орграф которого представлен на рис.1, можно перейти к эквивалентному детерминированному автомату, таблица переходов которого приведена в табл.5, а орграф на рис.4.

Из рис.1 нетрудно видеть, что в рассматриваемом примере «источниками недетерминированности» является всего два состояния - q₀ и q₁₀. Очевидно, что если «склеить» пару состояний {q₁ и q₃} и пару состояний {q₁₁ и q₁₇} образовав новые состояния q_1,3 и q_11,17, то недетерминированность устраняется.

Орграф на рис.4 задает все допустимые последовательности входных символов, которые соответствуют всем цепочкам терминалов, выводимых в данной грамматике.

Очевидно, что для определения с помощью распознающего автомата запрещенных последовательностей входных символов (невыводимых цепочек) орграф следует дополнить состоянием q₂₀ «Ошибка», в которое должны вести дуги, исходящие из всех остальных состояний автомата (в том числе и заключительного). Эти дуги должны быть помечены дизъюнкциями входных символов, отличных от символов, помечающих дуги, выходящие из данного состояния, или инверсией дизъюнкции этих символов, например, для состояния q_1,3 в состояние q₂₀ должна вести дуга, помеченная дизъюнкцией x₀ v x₂ v x₃ v x₄ v x₅ v x₆, или, иначе, (в силу ортогональности входных символов).

В орграфе (рис.4) этого не сделано, чтобы не усложнять картину, однако в табл.5 состояние q₂₀ «Ошибка» введено (последняя строка), и можно считать, что во все ее пустые клетки вписано состояние q₂₀. В этом случае табл.5 задает полностью определенный детерминированный конечный автомат.

Рис.4

Анализируя полученный граф, можно выявить девять цепочек переходов по графу: 51400; 5145; 5615; 56100; 700; 75; 36751; 3601; 37751; и три цепочки: 51403; 56103; 703; при которых происходит возвращение к начальному состоянию автомата S = q₀.