
Содержание отчета
Отчет составляется каждым студентом индивидуально и должен содержать:
наименование и цель работы;
исходные данные;
результаты расчетов показателей надежности и график функций P(t) в среде MATHCAD;
выводы по работе;
ответы на контрольные вопросы.
Контрольные вопросы
Как изменится надежность при последовательном соединении элементов системы с увеличением их числа?
Как определяется надежность последовательной системы в период нормальной эксплуатации?
Как изменится надежность системы, состоящей из параллельно соединенных элементов, при увеличении их числа?
Как определяется надежность параллельной системы, состоящей из равнонадежных элементов, в период нормальной эксплуатации?
Приложение 1
Пример выполнения лабораторной работы №4
Последовательная система
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
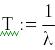
![]()
![]()
![]()
![]()

окончание прил. 1
Параллельная система
![]()
![]()
![]()
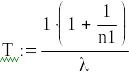
![]()
![]()
![]()
![]()

Лабораторная работа №5
Определение
надежности резервируемых систем
ЦЕЛЬ РАБОТЫ: определение показателей надежности резервируемых систем.
ОБОРУДОВАНИЕ: персональный компьютер с установленным программным продуктом MATHCAD.
ОСНОВНЫЕ СВЕДЕНИЯ
Общее резервирование с постоянно включенным резервом и с целой кратностью. При экспоненциальном законе распределения
![]() ;
;
![]() ;
;
 ,
,
где λ0
– интенсивность отказов основной или
любой резервной системы, равная
![]() .
.
Раздельное резервирование с постоянно включенным резервом и с целой кратностью. При экспоненциальном законе распределения, равнонадежных элементах и одинаковой кратности их резервирования
![]() ;
;
![]() ;
;
![]() ,
,
где λ – интенсивность отказов одного элемента системы.
Общее резервирование замещением с целой кратностью. При экспоненциальном законе распределения надежности нерезервированных систем
![]() ;
;
 ;
;
![]() ,
,
где
![]() .
.
Раздельное резервирование замещением с целой кратностью. При экспоненциальном законе распределения и равнонадежных элементах
![]() ;
;
 ;
;
где λ
– интенсивность отказов одного элемента,
![]() .
.
Порядок выполнения работы
Используя методические указания и рекомендуемую литературу, изучить основные показатели надежности определение показателей надежности резервируемых систем.
Используя оборудование выполнить задание по согласованию с преподавателем в соответствии с таблицей 3.
Таблица 3
№ |
Содержание задания |
1 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 1 000 часов при общем резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 2, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,6*10-3, 1/ч |
продолжение табл. 3
№ |
Содержание задания |
2 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 1 100 часов при общем резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 3, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,5*10-3, 1/ч |
3 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 1 200 часов при общем резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 4, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,4*10-3, 1/ч |
4 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 1 300 часов при общем резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 5, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,3*10-3, 1/ч |
5 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 1 400 часов при общем резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 6, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,2*10-3, 1/ч |
6 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 000 часов при раздельном резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 2, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,6*10-3, 1/ч |
продолжение табл. 3
№ |
Содержание задания |
7 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 200 часов при раздельном резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 3, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,5*10-3, 1/ч |
8 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 400 часов при раздельном резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 4, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,4*10-3, 1/ч |
9 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 600 часов при раздельном резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 5, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,3*10-3, 1/ч |
10 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 800 часов при раздельном резервировании с постоянно включенным резервом и с целой кратностью, если система имеет кратность резервирования m = 6, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,2*10-3, 1/ч |
11 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 000 часов при общем резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 2, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,6*10-3, 1/ч |
продолжение табл. 3
№ |
Содержание задания |
12 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 200 часов при общем резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 3, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,5*10-3, 1/ч |
13 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 400 часов при общем резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 4, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,4*10-3, 1/ч |
14 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 600 часов при общем резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 5, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,3*10-3, 1/ч |
15 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 2 800 часов при общем резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 6, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,2*10-3, 1/ч |
16 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 6 000 часов при раздельном резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 2, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,6*10-3, 1/ч |
окончание табл. 3
№ |
Содержание задания |
17 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 6 200 часов при раздельном резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 3, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,5*10-3, 1/ч |
18 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 6 400 часов при раздельном резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 4, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,4*10-3, 1/ч |
19 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 6 600 часов при раздельном резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 5, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,3*10-3, 1/ч |
20 |
Определить вероятность безотказной работы PС(t), интенсивность отказов и среднюю наработку до отказа системы за 6 800 часов при раздельном резервировании замещением с целой кратностью, если система имеет кратность резервирования m = 6, основная нерезервированная система содержит четыре равнонадежных последовательно соединенных элемента с интенсивностью отказов λ = 0,2*10-3, 1/ч |
СОДЕРЖАНИЕ ОТЧЕТА
Отчет составляется каждым студентом индивидуально и должен содержать:
наименование и цель работы;
исходные данные;
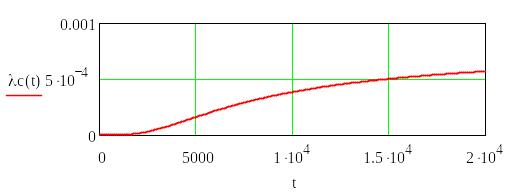
результаты расчетов показателей надежности и графики функций PС(t) и λ С(t) в среде MATHCAD;
выводы по работе;
ответы на контрольные вопросы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
В чем заключается информационное, временное и структурное резервирование?
Что понимают под общим и раздельным резервированием?
В чем заключается постоянное резервирование и резервирование замещением?
Чем отличаются ненагруженный, облегченный и нагруженный режимы резервирования?
Приложение 2
Пример выполнения лабораторной работы №5
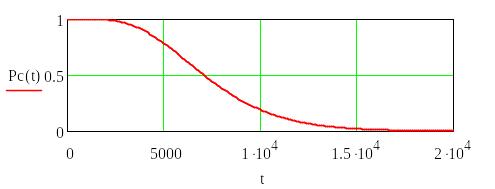
Система с общим резервированием с постоянно включенным резервом и с целой кратностью
![]()
![]()
![]()
![]()
![]()
![]()
![]()
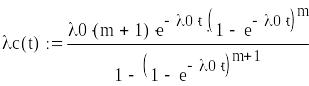
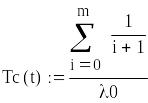
![]()
![]()
![]()


Продолжение прил. 2
Система с раздельным резервированием с постоянно включенным резервом и с целой кратностью
![]()
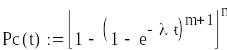
![]()

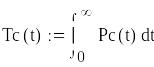
![]()
![]()
![]()

Продолжение прил. 2
Система с общим резервированием замещением
с целой кратностью
![]()
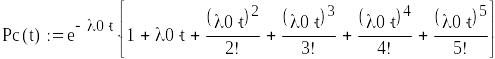
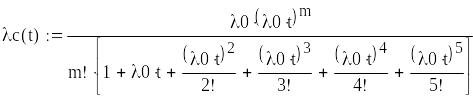
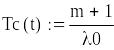
![]()
![]()
![]()
![]()
окончание прил. 2
Система с раздельным резервированием замещением
с целой кратностью
![]()
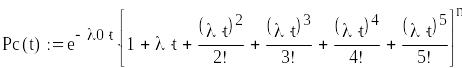
![]()
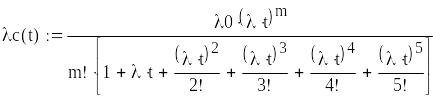
![]()
![]()
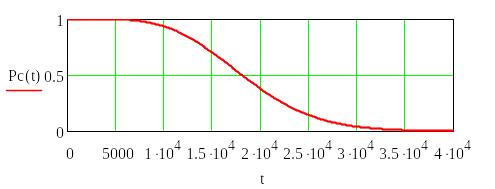
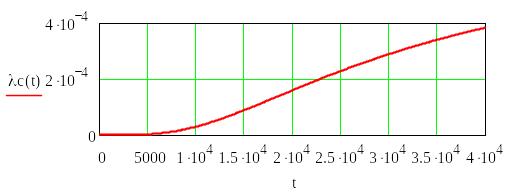
Лабораторная работа №6
Определение надежности восстанавливаемых элементов и изделий
ЦЕЛЬ РАБОТЫ: определение показателей надежности восстанавливаемых систем.
ОБОРУДОВАНИЕ: персональный компьютер с установленным программным продуктом MATHCAD.
ОСНОВНЫЕ СВЕДЕНИЯ
Для нерезервированной
восстанавливаемой системы независимо
от ее начального состояния (G0
или G1)
при
![]() вероятности P0(t)
и P1(t)
стремятся
к постоянным значениям:
вероятности P0(t)
и P1(t)
стремятся
к постоянным значениям:
![]() ;
;
![]() .
.
При экспоненциальных законах распределения времени наработки до отказа и времени восстановления случайный процесс работы восстанавливаемой системы после истечения некоторого времени стабилизируется, и вероятность застать систему работоспособной в произвольный момент времени остается постоянной. Система с указанным свойством называется эргодической, а сам процесс – марковским случайным процессом.
Случайный процесс называется марковским, если для любого момента времени вероятности всех состояний системы в будущем зависят только от ее состояния и не зависят от того, когда и как система перешла в это состояние. Переход системы из состояния в состояние происходит под воздействием потоков отказов и восстановлений. Если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими, то случайный процесс – марковский процесс.
Для различных типов дублированной системы (m=1) коэффициент готовности kГ имеет различные значения.
Для системы с постоянно включенным резервом и неограниченным восстановлением с графом состояний, представленным на рис. 13,
![]() .
.

Рис. 13
Для системы с постоянно включенным резервом и ограниченным восстановлением с графом состояний, представленным на рис. 14,
![]() .
.

Рис. 14
Для системы с резервированием замещением и неограниченным восстановлением с графом состояний, представленным на рис. 15,
![]() .
.

Рис. 15
Для системы с резервированием замещением и ограниченным восстановлением с графом состояний, представленным на рис. 16,
![]() .
.

Рис. 16
