Содержание

Лабораторная работа №4 14

Лабораторная работа №5 19

29

Лабораторная работа №6 30

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 36

Теоретические сведения

В настоящее время оценку надежности технических систем производят на основе методик, рекомендованных в межгосударственных стандартах ГОСТ 27.203-83 «Общие требования к методам оценки надежности по параметрам качества изготовляемой продукции», ГОСТ 27.204-83 «Технические требования к методам оценки надежности по параметрам производительности».

Технические системы с позиции надежности могут быть: последовательными, параллельными и комбинированными.

Простейшая расчетная модель системы из последовательно соединенных элементов приведена на рис. 1.

Рис. 1

При расчете надежности последовательной системы используем теорему умножения вероятностей, согласно которой вероятность совместного проявления независимых событий равна произведению вероятностей этих событий.

Тогда, вероятность безотказной работы системы равна произведению вероятностей безотказной работы отдельных элементов

.

Чем больше элементов включает в себя последовательная система, тем ниже вероятность ее безотказной работы.

В системе с параллельным соединением элементов (рис. 2) представляет интерес знание вероятности безотказной работы всей системы, системы без одного, без двух и т.д. элементов в пределах сохранения системой работоспособности даже при пониженных показателях.

Система из одинаковых элементов, соединенных параллельно, отказывает тогда, когда отказывают все ее элементы. В этом случае все элементы выполняют одну и ту же функцию, работают одновременно и равнонадежны.

По теореме умножения вероятностей вероятность отказа параллельной системы

,

Рис. 2

Тогда вероятность безотказной работы параллельной системы

.

Чем больше параллельных элементов содержит система, тем выше вероятность ее безотказной работы.

Надежность резервированных систем. Для достижения высокой надежности технических систем состоящих из элементов с ограниченным ресурсом вводят избыточность (резерв). Применяют: структурное, информационное и временное резервирование.

Информационное резервирование предполагает избыточное кодирование информации, которая используется в системе.

Временное резервирование возможно тогда, когда в процессе функционирования система имеет резерв времени, вследствие чего может осуществляться повторный расчет данных или другие контрольные процедуры.

Структурное резервирование заключается в использовании дополнительных элементов, которые при отказе основных элементов принимают на себя их функции. При этом возможно резервирование на уровне всей системы в целом (общее резервирование) или на уровне отдельных ее элементов (раздельное резервирование).

Структурное резервирование может осуществляться постоянно или замещением.

При постоянном структурном резервировании резервные элементы работают непрерывно во времени вместе с основными элементами в том же (нагруженном) режиме.

При резервировании замещением в случае отказа основного элемента его замещает один из резервных элементов. Резервные элементы могут находиться в ненагруженном, облегченном и нагруженном режимах.

При ненагруженном резерве резервные элементы находятся в выключенном состоянии и до момента их включения вместо основного элемента не могут отказать.

При облегченном резерве резервные элементы находятся в облегченном режиме до момента их включения вместо основного элемента. Во время ожидания в резерве они могут отказать, но с вероятностью меньшей вероятности отказа основного элемента.

При нагруженном резерве резервные элементы находятся в том же режиме, что и основной элемент, их надежность не зависит от того, в какой момент они включились вместо основного.

Общее резервирование с постоянно включенным резервом и с целой кратностью показано на рис. 3.

Рис. 3

Вероятность безотказной работы представленной на рис. 3 системы

Раздельное резервирование с постоянно включенным резервом и с целой кратностью показано на рис. 4.

Рис. 4

Вероятность безотказной работы представленной на рис. 4 системы

.

Общее резервирование с дробной кратностью и постоянно включенным резервом показано на рис. 5.

В этом случае, система «k из n» работоспособна, если работоспособны не менее k элементов из n. Кратность резервирования .

Для определения вероятности безотказной работы P(t) применим метод полной группы событий. Система работоспособна, если за время t осуществляется одно из событий: A₀ – все элементы исправны; A₁ – один элемент отказал, (n – 1) элементов исправны; … A_k – (n – k) элементов отказали, k элементов исправны. Общее число таких событий равно , а вероятность события A_i (если все элементы равнонадежны):

.

Рис. 5

Общее резервирование замещением с целой кратностью показано на рис. 6.

В этом случае работает только одна основная система, остальные системы отключены с помощью специальных переключающих устройств и находятся в «холодном» резерве. При отказе основной системы она отключается, а на ее место подключается одна из резервных систем. Таким образом, резервированная система откажет при возникновении (m+1)-го отказа. Предполагается, что системы, находящиеся в резерве, отказывать не могут и что переключающие устройства абсолютно надежны.

Раздельное резервирование замещением с целой кратностью показано на рис. 7.

Вероятность безотказной работы представленной на рис. 7 системы

,

где P_i(t) – вероятность безотказной работы системы из-за отказов элементов i-го типа, резервированных по способу замещения.

Рис. 6

Рис. 7

Раздельное резервирование замещением с дробной кратностью показано на рис. 8.

Этот вид резервирования применяется, если все элементы системы выполняют одинаковые функции. Основная система имеет n элементов, а m элементов находятся в «холодном» резерве. При отказе любого работающего элемента на его место подключается любой из резервных. Кратность резервирования – m/n.

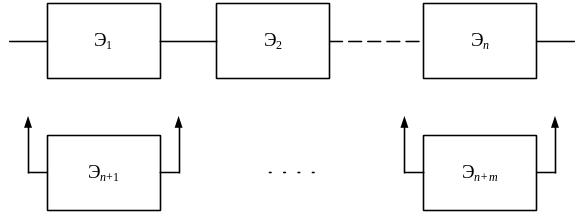
Рис. 8

Надежность нерезервированных восстанавливаемых систем. Нерезервированная восстанавливаемая система в произвольный момент времени может находиться в одном из двух состояний: работоспособном (G₀) и неработоспособном (G₁). Процесс ее функционирования можно отразить графом состояний, представленным на рис. 9. Из состояния G₀ в состояние G₁ система переходит в результате отказов с интенсивностью λ, а из G₁ в G₀ – в результате восстановления с интенсивностью μ.

Рис. 9

При простейших потоках отказов и восстановлений λ=const и μ=const. Последнее равенство означает, что производительность труда ремонтника постоянна и не зависит от времени. Поэтому время восстановления имеет экспоненциальное распределение:

;

.

Основным показателем надежности нерезервированной восстанавливаемой системы является коэффициент готовности k_Г.

Пусть P₀(t) и P₁(t) – вероятность того, что в момент времени t система находится в состояниях G₀ и G₁. Тогда и коэффициент готовности .

Если в начальный момент времени система работоспособна (состояние G₀), и , то

;

.

На рис. 10 представлены графики показателей надежности нерезервированной восстанавливаемой системы, находящейся в начальный момент в состоянии G₀.

Рис. 10

Если в начальный момент времени система неработоспособна (состояние G₁), и , то

;

.

На рис. 11 представлены графики показателей надежности нерезервированной восстанавливаемой системы, находящейся в начальный момент в состоянии G₁.

Рис. 11

Надежность резервированных восстанавливаемых систем. Резервирование с восстановлением является эффективным средством повышения надежности, с помощью которого можно добиться сколь угодно высокой надежности.

Резервированная восстанавливаемая система в произвольный момент времени может находиться в одном из трех состояний: исправном (G₀), неисправном, работоспособном (G₁) и неработоспособном (G₂). Процесс ее функционирования отражает граф состояний, представленный на рис. 12. Из состояния G₀ в состояние G₁ и в состояние G₂ система переходит в результате отказов с интенсивностью λ₀₁ и λ₀₂ соответственно, из G₁ в G₂ – в результате G₀ – отказов с интенсивностью λ₀₂, а из G₁ и G₂ в G₀ – в результате восстановления с интенсивностью µ₁₀ и µ₂₀.

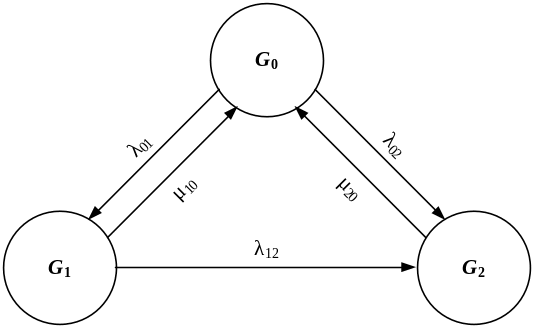
Рис. 12

Основным показателем надежности резервированной восстанавливаемой системы также является коэффициент готовности k_Г.

Лабораторная работа №4

Определение надежности систем, состоящих из

последовательно и параллельно соединенных элементов

ЦЕЛЬ РАБОТЫ: определение показателей надежности систем, состоящих из последовательно и параллельно соединенных элементов.

ОБОРУДОВАНИЕ: персональный компьютер с установленным программным продуктом MATHCAD.

ОСНОВНЫЕ СВЕДЕНИЯ

В период нормальной работы для последовательной системы, состоящей из n элементов, справедлив экспоненциальный закон надежности

,

где λ_С – интенсивность отказов системы.

Интенсивность отказов последовательной системы

.

Средняя наработка до отказа последовательной системы

В период нормальной работы для параллельной системы, состоящей из m элементов, справедлив экспоненциальный закон надежности

.

Средняя наработка до отказа параллельной системы

.