Правило большинства в многомерном случае

В 1948 г. Дункан Блэк показал, что если индивидуальные пред­почтения являются одновершинными, то наибольшую поддержку обычно получает вариант медианного избирателя. Отложим по оси абсцисс количество общественного блага, а по оси ординат полез­ность, получаемую от него различными избирателями (см. рис. 4.5). Функции полезности отдельных индивидов, соответствую­щие их предпочтениям относительно объемов производства обще­ственного блага, обозначим V₁ V₂, V₃, V₄, V₅. Очевидно, что наи­большую поддержку получит проект, находящийся в середине этого набора предпочтений. При голосовании по принципу просто­го большинства голос медианного избирателя окажется решаю­щим в кооперации либо со сторонниками ограничения производ­ства общественных благ: (V₁ + V₂) + V₃, либо в кооперации с теми, кто настаивает на расширении их производства: (V₅ + V₄) + V₃.

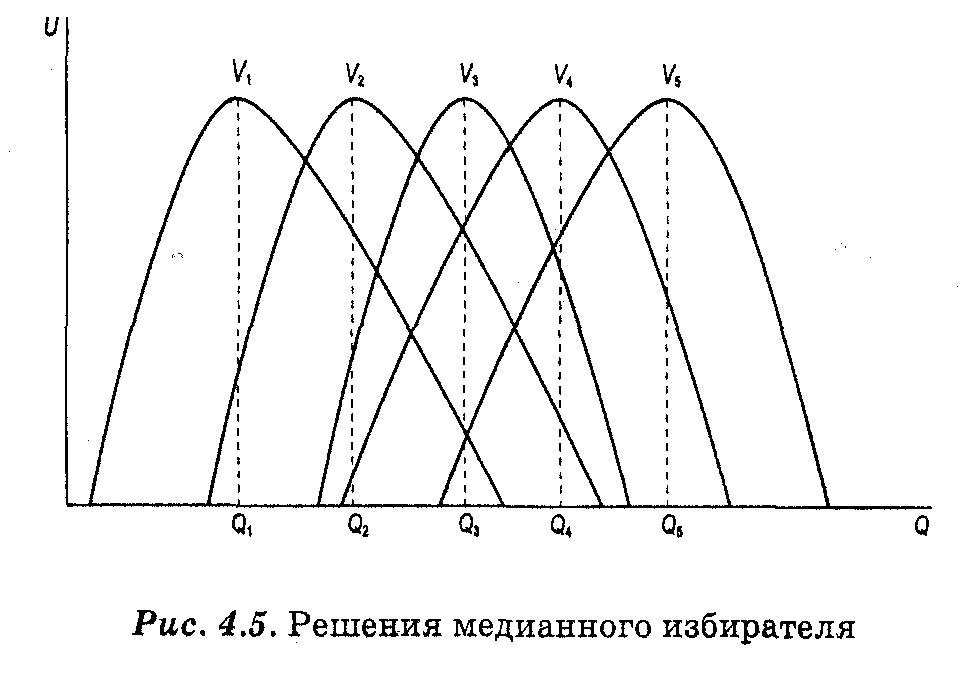
Однако не всегда предпочтения избирателей можно отобразить на одной шкале, как в случае, представленном на рис. 4.5. В жизни гораздо чаще встречаются многомерные варианты, когда надо принимать решения сразу по нескольким вопросам.

Проиллюстрируем это на примере двух общественных благ: Х₁ и Х₂. Допустим сначала, что в выборе участвуют только два избирателя – Андреев и Борисов. Допустим, что замкнутые кривые U_A¹, U_A², U_A³ и т.д. отражают равноценные, с точки зрения Андре­ева, альтернативы, a U_Б¹, U_Б ², U_Б³ и т.д. — равноценные альтерна­тивы Борисова. Очевидно, что все множество Парето-оптимальных решений будет лежать на контрактной линии, соединяющей Аи Б. Если минимально допустимым уровнем полезности являют­ся кривые U_A² и U_Б², то тогда допустимое множество решений проб­лемы составит заштрихованная область на рис. 4.6. При этом не исключено, что кто-то из голосующих может получить большую выгоду за счет других. Например, А удастся переместиться в точ­ку F или Б в точку D.

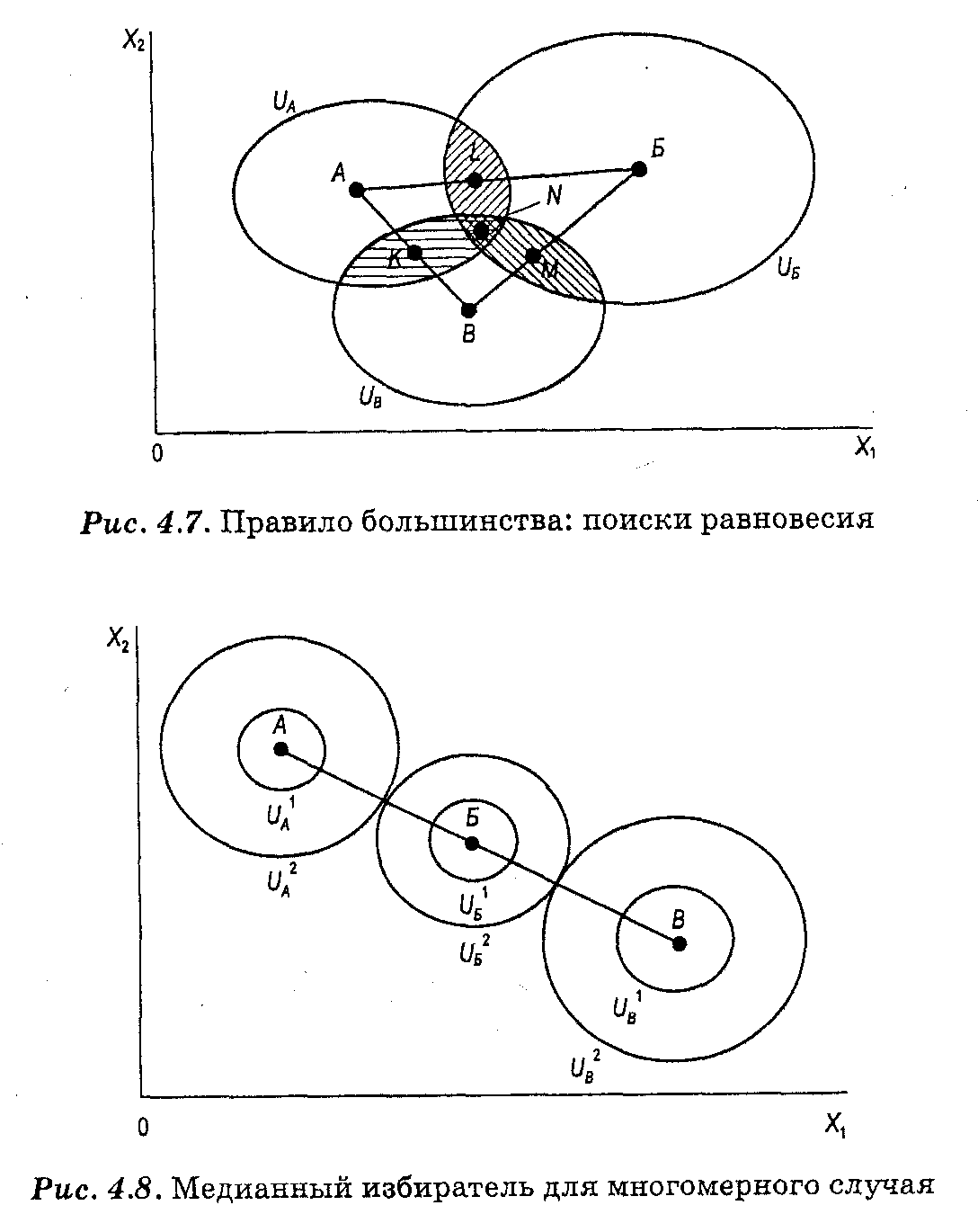
Предположим теперь, что в выборе участвуют три избирате­ля — Андреев, Борисов и Васильев. Отразим предпочтения на­ших избирателей точками А, Б и В. Равновесие может быть дос­тигнуто между ними в окрестностях точки N (см. рис. 4.7). Од­нако возможно создание коалиции. Если, например, Андреев и Васильев договорятся, то они могут предложить вариант К, ко­торый для них выгоднее, чем N.

Наконец, возможен и такой случай, когда предпочтения одно­го из избирателей, например Борисова, находятся между интере­сами Андреева и Васильева (см. рис. 4.8). В этом случае любые принимаемые решения будут на благо этому избирателю, а его го­лос окажется решающим при принятии каждого из них. Таким образом, выводы относительно медианного избирателя могут быть распространены с одномерного на многомерный случай.

Выше мы разобрали позитивный аспект правила большинства. Однако в силу своей широкой распространенности оно имеет и нор­мативный смысл. Многими людьми это правило воспринимается как наиболее справедливый путь решения важных проблем. Так ли это на самом деле? Попытаемся ответить на этот вопрос.

4.3. Правило большинства: нормативная характеристика Теорема Мэя о правиле большинства

Кеннет Мэй первым сделал попытку обосновать соответствие пра­вила большинства принципам справедливости и равенства. В изве­стной теореме Мэй определяет функцию коллективного решения в виде D = f (D_1; D₂, ..., D_n) где п — число индивидов в группе.

Каждое D_i принимает значения 1, 0, -1 («за», «воздержался» и «против» соответственно), отражающие его предпочтения для каж­дой пары вопросов xP_iу, xI_i у, yP_ix, где Р (preference) означает стро­гое предпочтение, I (indifference) — безразличие, или равноцен­ность двух альтернатив, a R (reference) — нестрогое предпочтение. Обозначим нестрогие предпочтения i-го индивида как xR_iy и кол­лектива в целом — xRy. Правило простого большинства интерпрети­руется следующим образом:

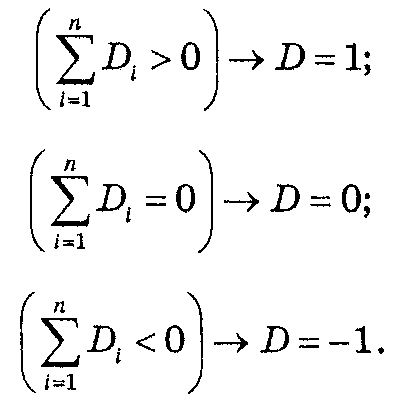
Такая запись позволяет сформулировать правило простого большинства в форме теоремы.

Теорема. Функция группового выбора представляет собой правило простого большинства, если оно удовлетворяет следую­щим четырем условиям (подразумеваемым самим понятием пра­вила простого большинства).

1. При каждом добавлении к целому функция принятия реше­ния принимает значения -1, 0 или 1 и поэтому является дискрет­ной. Фактически это аксиома однозначности: при данном наборе предпочтений функция решений коллектива означает выбор наи­лучшего значения (либо х, либо у, либо равнозначность обоих вари­антов).

2. Изменение любого значения 1 на -1 и -1 на 1 оставляет сумму неизменной. Вторая аксиома фактически равнозначна признанию анонимности принимаемых решений: сдвиг предпоч­тений одного из членов группы (например, от xP_iу к yP_ix) и ответ­ный сдвиг любого другого (например, от yP_jx к хР_jу) оставляет ко­нечный результат рассматриваемой группы неизменным. Поэтому неважно, кто именно принял это конкретное решение.

3. Если ранжирование остается неизменным для любых двух пар альтернатив, то таким же оно будет и при суммировании го­лосов. Третья аксиома говорит о нейтральности предпочтений. Допустим, в данной группе х > у, поэтому если индивиды анализи­руют z и w, как х и у, то z должно предпочитаться w (z >w).

Если ∑D_i = 0 , увеличение любого D_i делает ∑D_i >0 u приносит победу некоторому х. Если ∑D_i > 0 увеличение любого D_i оставит ∑D_i > 0 и не изменит исхода выборов. Четвертая аксиома говорит о том, что существует свойство положительного реагирования (или позитивного отклика): если в качестве итогового решения приня­то xRy, и предпочтения одного из участников изменяются, напри­мер, от yR_iх к xR_iу или от xI_i у к хР_iу, то при неизменности пред­почтений всех других членов группы результат коллективного ре­шения должен содержать хРу.

Покажем, что правило большинства действительно удовлет­воряет всем четырем аксиомам. Сначала проиллюстрируем это для трех первых условий.

[ N(-1) = N(1)] D = ∑D_i = 0, (4-6)

где N(-l) — это число голосов за у, а N(1) — за х.

Предположим, что не выполняется условие

[ N(-l) = N(l)] D = ∑D_i = l. (4-7)

Когда число голосов за у равно числу голосов за х, достигается ре­зультат х.

Переобозначим теперь у в z, a х в w, где голос за z записывает­ся как -1, а голос за w как 1. Поменяем все 1 на -1, а -1 на 1.

По условию независимости последнее изменение не должно повлиять на групповое решение. Все индивиды, относящиеся к х по меньшей мере так же хорошо, как к у (xR_iy), теперь будут отно­ситься к 2 по меньшей мере так же хорошо, как к w. По аксиоме нейтральности, выиграть выборы в результате должен z, если он изначально был х, но z эквивалентен у, а не х. Аксиома однознач­ности нарушена.

Таким образом, выражение (4-7) противоречит первым трем аксиомам. Аналогично можно показать, что выражение (4-8) не­совместимо с первыми тремя аксиомами:

[ N(-l) = N(l)] D = -l. (4-8)

Иными словами, должно выполняться уравнение (4-6).

Из (4-6) и по аксиоме позитивного отклика следует, что

[ N(1) = N(-1) + 1] D = 1. (4-9)

Когда число голосов за х на единицу больше, чем число голо­сов за у, х должен выиграть. Теперь предположим, что когда чис­ло голосов за х на т - 1 больше, чем за у, побеждает х. Измене­ние в предпочтениях одного избирателя меняет разрыв между те­ми, кто предпочитает х, и теми, кто предпочитает у, на величину т (х больше у на m), и это не меняет исход вследствие позитивно­го отклика. Таким образом, четыре приведенных условия озна­чают правило простого большинства.

Теорема Мэя позволяет сделать любопытные выводы. Преж­де всего, если мы начинаем с каких-то правил голосования и четко определим условия, которым они должны удовлетворять, станет очевидным, что по мере увеличения наших требований число реальных кандидатов, соответствующих им, будет сокра­щаться. В частности, Мэй наглядно показал, что при четком вы­полнении сформулированных им правил набор возможных аль­тернатив сокращается до единственного правила простого боль­шинства.

Нормативный характер приведенных выше аксиом позволяет сделать вывод, что эти нормативные черты присущи и самому пра­вилу простого большинства. Нормативный аспект заключен во второй и третьей аксиомах (анонимности и нейтральности).

Характеристика нейтральности как независимости предпочте­ний получила дальнейшее развитие в работах Амартьи Сена. Фак­тически мы абстрагируемся от эффекта присоединения к большин­ству, «эффекта сноба» и т.д., а также от интенсивности предпочте­ний. Нейтральность фактически означает, что подход к любому выбору одинаков, независимо от того, о чем идет речь: о наказании за мелкое хулиганство или о вынесении смертного приговора. Вполне очевидно, что в последнем случае предпосылка о равной ин­тенсивности предпочтений, оправдывающая анонимность, являет­ся неправомерной.