4.2. Правило большинства: позитивный подход Оптимальное большинство

Для того чтобы снизить издержки принятия решений, связанные с правилом единогласия, используют более простые процедуры, например правило большинства. Дж. Бьюкенен и Г. Таллок пред­ложили довольно простую модель, которая показывает, как опре­деляется оптимальное большинство (см. рис. 4.1).

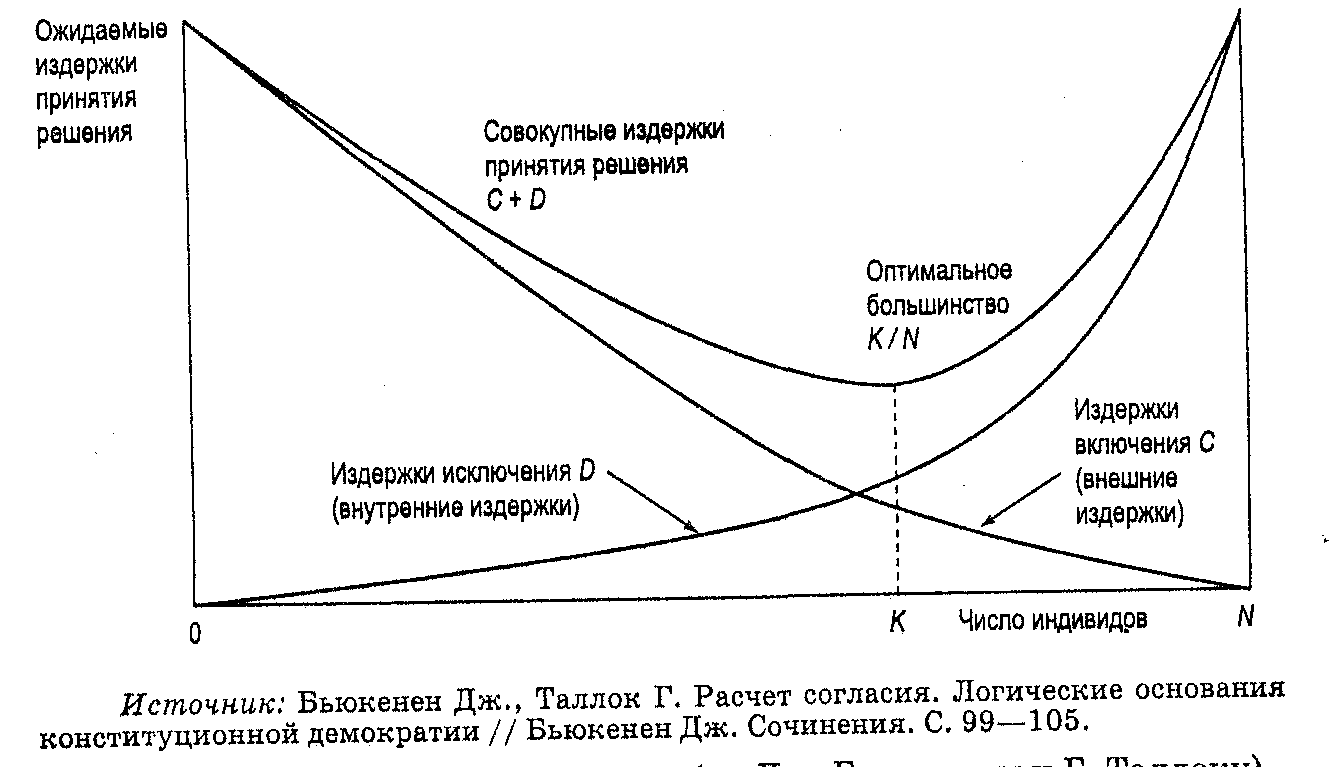
Рис. 4.1. Оптимальное большинство (по Дж. Бьюкенену и Г. Таллоку)

Отложим по оси ординат ожидаемые издержки принятия ре­шений, а по оси абсцисс число индивидов, согласие которых необ­ходимо для осуществления коллективного действия. Тогда издерж­ки, которые несет коллектив при принятии решения, можно раз­делить на две основные группы: внутренние и внешние.

Пусть функция D отражает внутренние издержки, т.е. издерж­ки, заключающиеся в отклонении уровней полезности от тех значе­ний, которые могли быть достигнуты при единогласном принятии решений. Функция затрат принятия решений — это функция вида D_i = f(N_a), где D_i — текущие издержки, которые i-й индивид ожидает понести вследствие участия в коллективных решениях по какому-либо виду деятельности. Если для принятия одного решения требу­ется согласие двух или более индивидов, то необходимы время и уси­лия для достижения такого согласия. Затраты возрастают по мере увеличения размеров группы, необходимой для принятия решений. Чем больше людей входит в состав группы, тем больше будут изде­ржки, потому что требуется дополнительное время, чтобы согласо­вать все интересы. По мере приближения к единогласию происходит резкое увеличение ожидаемых затрат принятия решений.

Функция внешних затрат — это функция типа C_i = f(N_a), где N_a — число индивидов (из группы с общим числом N), которые должны прийти к согласию для того, чтобы было принято решение о коллективных действиях. В самом деле, чтобы коллективные действия осуществились, индивид должен затратить какое-то вре­мя и усилия для выработки коллективного решения и достижения согласия со своими коллегами по группе. По мере увеличения чис­ла индивидов, чье согласие необходимо получить, ожидаемые внешние затраты снижаются. Если соблюдается правило едино­гласия, то затраты, ожидаемые индивидом, должны быть равны нулю, поскольку он добровольно не позволит, чтобы действия дру­гих обусловливали его внешние затраты (раз он может это пред­отвратить). Поэтому кривая С показывает внешние издержки, сокращающиеся по мере приближения к N, т.е. ожидаемые поте­ри полезности в связи с прохождением решения, которое ухуд­шает положение части членов группы.

Рациональный индивид в момент конституционного выбора попытается выбрать такое правило принятия решений, которое позволит ему минимизировать текущую стоимость ожидаемых затрат, связанных с его принятием. Он сможет этого достичь пу­тем минимизации суммы ожидаемых внешних и внутренних зат­рат. Геометрически это означает суммирование по вертикали обе­их этих функций, и тогда суммарные издержки будут равны С + D. Они достигают минимума, когда для принятия решения требуется К голосов. Оптимальное большинство определяется таким количе­ством участников голосования, при котором минимизируется сум­ма обоих видов издержек. Оптимальное большинство будет равно K/N. Естественно, что для каждой группы людей, голосующих по конкретному вопросу, будет свое оптимальное большинство. Если мнения членов группы совпадают, то внешние издержки будут относительно невелики. Поэтому правило простого большинства яв­ляется оптимальным для группы, у которой альтернативные изде­ржки времени имеют относительно большое значение. Если пред­почтения членов группы сильно расходятся друг с другом, возрас­тают потенциальные потери, возникающие в случае игнорирова­ния мнений участников переговорного процесса. Простое больши­нство достигается в ситуации, когда требуется одобрение, равное (N/2) + 1, т.е. 50% голосов плюс один голос.

Действительно, если для принятия решения требуется менее 50% голосов, то существует опасность одновременного (или после­довательного) голосования за два взаимоисключающих варианта. Это сильно затягивает принятие окончательного решения. Допус­тим, сегодня собирается один состав депутатов, и он принимает ре­шение одобрить проект, а завтра — другой, и голосует против него. Рассмотрим простой пример. Существуют четыре группы из­бирателей разной численности: первая группа — 4 избирателя, вторая — 6, третья — 7 и четвертая — 8. Предположим, что есть всего 4 кандидата: Андреев (А), Борисов (Б), Васильев (В) и Гаврилов (Г). Предпочтения каждой из групп представлены в табл. 4.1.

Таблица 4.1