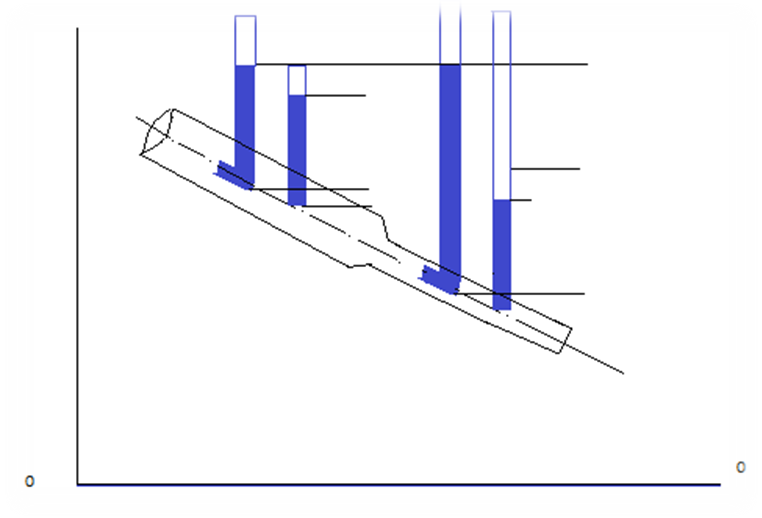
Иллюстрация применения уравнения Бернулли.

1

2

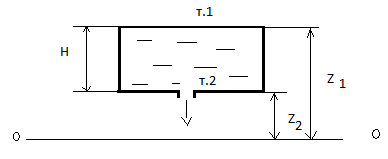
Установим в 2-х поперечных сечениях наклонного трубопровода две вертикальные открытые «пьезометрические» трубки, у одной из которых конец загнут навстречу потоку жидкости.

В прямых вертикальных (незагнутых) трубках жидкость поднимается на высоту, отвечающую гидростатическому давлению в местах их погружения, т.е. эти трубки измеряют статический напор.

В трубках с загнутыми концами уровень жидкости будет выше и показывает сумму статического и динамического напоров. Согласно уравнению Бернулли, жидкость в загнутых трубках в сечениях 1 и 2 поднимается на одну и ту же высоту.

П оскольку > ; ; > ; < ;

В точке, где скорость больше, давление меньше.

Скоростной напор – это разность показаний трубок.

Взаимный переход потенциальной и кинетической энергий и постоянство их суммы.

Хотя уравнение Бернулли получено для ограниченных условий (для идеальной жидкости и установившегося движения), оно позволяет решать основную задачу движения жидкости, связывая скорость и давление.

При движении реальной жидкости начинают действовать силы внутреннего трения и силы трения о стенку трубы. На преодоление возникающего гидравлического сопротивления должна тратиться часть энергии потока (и на потери тепла).

При этом имеем: + + ;

Для реальных жидкостей уравнение Бернулли приобретает вид:

- потерянный напор, характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.

Определение потерь напора является практически важной задачей. Решение дифференциальных уравнений реальных жидкостей, как правило, невозможно.

В качестве практического приложения уравнения Бернулли можно рассмотреть определение скоростей и расходов и времени истечения жидкостей из резервуаров.

1. Истечение жидкостей.

1) Истечение через круглое отверстие в тонком днище при постоянном уровне:

Весь статический напор переходит в кинетическую энергию, т.е. расходуется на создание скорости.(через узкое сечение вытекает струя).

Запишем уравнение Бернулли (для идеальной жидкости):

;

Для открытого сосуда: ; при постоянном уровне 0;

Пренебрегая расстоянием от плоскости отверстия до узкого сечения:

; ;

Следовательно: ; для идеальной жидкости.

При движении реальной жидкости часть напора Н теряется на трение и преодоление сопротивления, вызванного внезапным сужением потока в отверстии.

Для реальной жидкости:

!!!Скорость в узком сечении: ; где: - коэффициент скорости (ϕ ).

Т.к. площадь струи в отверстии больше, чем в самом узком сечении, скорость жидкости в отверстии меньше, чем в узком сечении

; где: Ɛ= коэффициент сжатия струи.

коэффициент расхода, он определяется опытным путём (зависит от Re, формы отверстия и свойств жидкости).

Объёмный расход при истечении:

к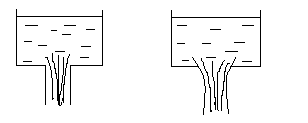 оноид увеличивает Ɛ и ϕ;

ϕ

Ɛ 0,64;

Вакуум расширяет струю.

! !! Для воды

Следовательно, расход жидкости, вытекающей из отверстия в тонком днище, зависит от высоты постоянного уровня жидкости над отверстием и от размера отверстия, но не зависит от формы сосуда.

Это управление применимо для определения расхода жидкости, вытекающей из отверстия в тонкой боковой стенке.

При истечении через насадок (короткий цилиндрический патрубок) происходит дополнительная потеря напора на входе и выходе (ϕ снижается), зато Ɛ 1, т.к. поток заполняет сечение за счёт вакуума.

2) Истечение через отверстие в тонком днище при переменном уровне с целью определения времени опорожнения сосуда.

S

dH

H

Уровень Н снижается, скорость W уменьшается во времени нестационарный процесс.

Определим время уменьшения уровня от до :

За бесконечно малый промежуток времени d , уменьшением уровня можно пренебречь, и объём вытекающей жидкости:

dV=

За тот же промежуток d уровень жидкости понизится на бесконечно малую величину dH и убыль жидкости (при S=const):

dV=-SdH;

Согласно уравнению неразрывности, приравниваем:

;

d ;

Принимая, что коэффициент расхода не зависит от скорости истечения ( ), интегрируем:

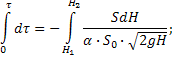
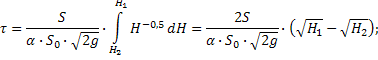
В случае полного опорожнения резервуара и:

При переменном поперечном сечении S=f(H) при интегрировании эта зависимость должна быть учтена (ж/д цистерна, коническое хранилище и др.).

Для обеспечения постоянной скорости истечения и расхода при изменении уровня жидкости, в лабораторной практике применяют сосуд Мариотта:

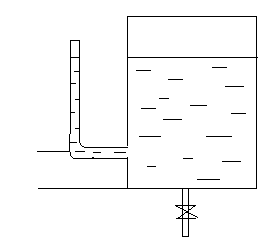
Трубка соединяется с атмосферой. При истечении образуется вакуум и через трубку поступает воздух.

На уровне входа трубки в сосуд в соответствии с законом Паскаля поддерживается атмосферное давление, а, следовательно, и постоянный напор Н.

Скорость истечения постоянна, пока жидкость не достигнет уровня входа трубки.