Режимы движения жидкости.

Впервые изучено Рейнольдсом (1883 г.) подкрашиванием жидкости, вытекающей при постоянном уровне.

Различают: Ламинарное движение => все частицы жидкости движутся по параллельным траекториям и турбулентное движение => отдельные частицы жидкости движутся по хаотическим траекториям, в то время как вся масса жидкости в целом перемещается в одном направлении.

Особенностью турбулентного потока является наличие поперечных перемещений частиц жидкости, приводящих к интенсивному перемешиванию потока по сечению. Для этого требуется большая затрата энергии.

Режим движения жидкости количественно характеризуется значением критерия (безразмерный комплекс).

Критерий Re является мерой соотношения между силами вязкости и инерции в движущемся потоке.

Вероятность турбулизации возрастает с уменьшением вязкости жидкости и с увеличением плотности (мера инерционного отклонения от прямолинейной траектории частиц).

Переход от ламинарного течения происходит скачкообразно, характеризуется критическим значением Re.

По прямым гладким трубам .

При Re<2320 => устойчивый ламинарный режим.

2320<Re<10000 => режим течения неустойчивого турбулентного или переходного (смешанный): при этом может наблюдаться с меньшей вероятностью ламинарное течение.

Re>10000 => устойчивая (развитая) турбулентность.

При движении жидкости через каналы некруглого сечения при расчёте Re используют эквивалентный диаметр:

=4 ;

Гидравлический радиус – отношение площади свободного сечения трубопровода или канала, через которое протекает жидкость, к смоченному периметру:

Для круглой трубы: ;

Квадрата:

Канала прямоугольного сечения: = ;

Кольцевого сечения:

В критерий Re входит (как и в уравнение расхода) средняя ёмкость, а действительные скорости различны по сечению, причём их распределение различно для ламинарного и турбулентного течений.

Для ламинарного потока вид распределения скоростей может быть установлен теоретически.

Распределение скоростей и расход жидкости при установившемся ламинарном потоке

Выделим в потоке жидкости, ламинарно движущемся по трубе радиусом R, цилиндрический слой длиной L и радиусом r ,причём скорость движения жидкости на расстоянии r равна

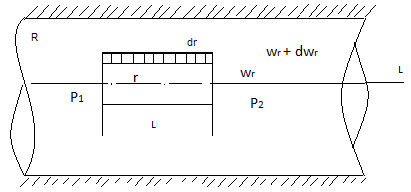
Движение слоя жидкости происходит под действием разности сил давления с обеих сторон цилиндра:

где гидростатические давления.

Одновременно движению цилиндра оказывает сопротивление сила внутреннего трения, действующая по поверхности:

Т=- ; где: F=2 - наружная поверхность цилиндра (знак «-» указывает на убывание скорости с увеличением радиуса: по направлению к стенке).

При установившемся потоке имеем:

( ) ; разделяя переменные и интегрируя:

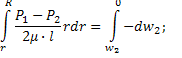
Или: ; (1)

Отсюда следует, что скорость имеет максимальное значение на оси трубы, где r=0;

Отсюда: = (2)

Сопоставляя (1) и (2), находим:

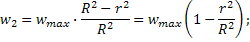
Это закон Стокса, выражающий параболическое распределение скоростей в сечении трубопровода при ламинарном движении.

Эпюра скоростей имеет вид:

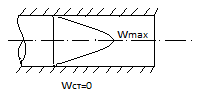
Определим расход жидкости через трубу:

Выделим кольцевое сечение толщиной dr и окружностью 2 .

Расход через кольцевое сечение:

d =

интегрируем: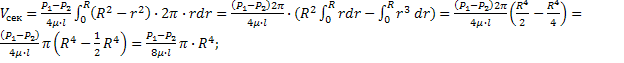

Уравнение Пуазейля.

С другой стороны:

Отсюда средняя скорость:

!!!!!!

При ламинарном течении средняя скорость равна половине максимальной (по оси трубы)!!!!!