B1	9
B2	45
B3	-4
B4	1230
B5	-7
B6	6
B7	2
B8	5
B9	9
B10	0,9
B11	7,5
B12	2,4
B13	20
B14	9

Решения

Задание 1

Студент получил свой первый гонорар в размере 700 рублей за выполненный перевод. Он решил на все полученные деньги купить букет тюльпанов для своей учительницы английского языка. Какое наибольшее количество тюльпанов сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, тюльпаны стоят 60 рублей за штуку и букет должен состоять из нечетного числа цветов? Решение. Налог составит 700   0,13 = 91 рубль. После выплаты налога останется 700 − 91 = 609 рублей. Разделим 609 на 60:

.

Значит, денег хватает на 10 тюльпанов. В букете должно быть нечетное число цветов, поэтому студент купит 9 тюльпанов.

Ответ: 9.

Задание 2

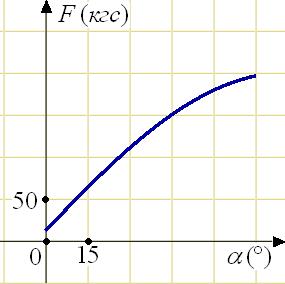В аэропорту чемоданы пассажиров поднимают в зал выдачи багажа по транспортерной ленте. При проектировании транспортера необходимо учитывать допустимую силу натяжения ленты транспортера. На рисунке изображена зависимость натяжения ленты от угла наклона транспортера к горизонту при расчетной нагрузке. На оси абсцисс откладывается угол подъема в градусах, на оси ординат – сила натяжения транспортерной ленты (в килограммах силы). При каком угле наклона сила натяжения достигает 150 кгс? Ответ дайте в градусах. Решение. Из графика видно, что сила натяжения достигает 150 кгс при угле наклона 45 градусов.

Ответ: 45.

Задание 3

Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B(6; 4) и параллельной прямой, проходящей через начало координат и точку A(6; 8). Решение. Уравнение прямой имеет вид: , где  — угловой коэффициент. Тогда , подставляя значения абсцисс и ординат точек и , решая уравнения одновременно, получаем:

.

Так как прямые параллельны, то

.

Теперь подставляя значения и точку с координатами , зная еще, что координата второй точки, принадлежащей прямой, , находим .

Ответ: −4.

Задание 4

В таблице даны тарифы на услуги трех фирм такси. Предполагается поездка длительностью 70 минут. Нужно выбрать фирму, в которой заказ будет стоить дешевле всего. Сколько рублей будет стоить этот заказ?

Фирма такси	Подача машины	Продолжительность и стоимость минимальной поездки *	Стоимость 1 минуты сверх продолжительности минимальной поездки
А	350	Нет	13
Б	Бесплатно	20 мин. — 300 руб.	19
В	180	10 мин — 150 руб.	15

Если поездка продолжается меньше указанного времени, она оплачивается по стоимости минимальной поездки. Решение. Рассмотрим различные варианты. Стоимость поездки на такси фирмы A будет складываться из стоимости 70 минут поездки, то есть 70   13 = 910 руб., а также стоимости подачи такси и будет составлять 350 + 910 = 1 260 руб. Стоимость поездки на такси фирмы Б будет складываться из стоимости минимальной поездки, а также стоимости 50 минут поездки сверх минимальной, то есть 300 + 50   19 = 300 + 950 = 1 250 руб. Стоимость поездки на такси фирмы В будет складываться из стоимости минимальной поездки, а также стоимости 60 минут поездки сверх минимальной и стоимости подачи машины, то есть 150 + 60   15 + 180 = 330 + 900 = 1230 руб.

Ответ: 1230.

Задание 5

Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней. Решение.

Ответ:  −7.

Задание 6

Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6? Решение. значит, треугольник – равносторонний.

Ответ: 6.

Задание 7

Найдите значение выражения . Решение.

= .

Ответ: 2.

Задание 8

На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек экстремума функции на отрезке . Решение. Точки экстремума соответствуют точкам смены знака производной — изображенным на графике нулям производной. Производная обращается в нуль в точках −6, −2, 2, 6, 9. На отрезке функция имеет точек экстремума.

Ответ: 5.

Задание 9

В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна 2; объем пирамиды равен 6. Найдите длину отрезка . Решение. отрезок высотой треугольной пирамиды , ее объем выражается формулой

Таким образом,

Ответ: 9.

Задание 10

Маша включает телевизор. Телевизор включается на случайном канале. В это время по трем каналам из тридцати показывают телевикторины. Найдите вероятность того, что Маша попадет на канал, где телевикторины не идут. Решение. телевикторины не идут по 30 – 3 = 27 каналам. Тогда вероятность того, что Маша попадет на канал, где телевикторины не идут, равна

.

Ответ: 0,9.

Задание 11

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба. Решение. Площадь поверхности получившегося многогранника равна сумме площадей поверхностей куба со стороной 1 и параллелепипеда со сторонами 1, 0,5,  0,5 минус 4 площади основания вырезанной призмы:

.

Ответ: 7,5.

Задание 12

Расстояние (в км) от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле , где  км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров? Решение. Задача сводится к решению уравнений и при заданном значении R:

Следовательно, чтобы видеть горизонт на более далеком расстоянии, наблюдателю нужно подняться на метра.

Ответ: 2,4.

Задание 13

От пристани к пристани отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 1 км/ч большей отправился второй. Расстояние между пристанями равно 420 км. Найдите скорость первого теплохода, если в пункт оба теплохода прибыли одновременно. Ответ дайте в км/ч. Решение. Пусть км/ч – скорость первого теплохода, тогда скорость второго теплохода по течению равна км/ч. Первый теплоход находился в пути на 1 час больше, чем второй, отсюда имеем:

Ответ: 20.

Задание 14

Найдите точку максимума функции . Решение. Найдём производную заданной функции:

.

Найдем нули производной:

.

Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума .

Ответ: 9.

Проверка части С

Начало формы

Содержание критериев оценивания задачи С1	Баллы
Обоснованно получен верный ответ.	2
Решение не содержит логических пробелов, получен ответ, неверный, но только из-за вычислительной ошибки или описки.	1
Все прочие случаи.	0

А) Решите уравнение

Б) Укажите корни уравнения, принадлежащие отрезку

Решение.

А) Преобразуем уравнение, получаем Значит, или где В первом случае во втором случае где Первая серия решений входит во вторую. Б) Отметим решения на тригонометрической окружности. Отрезку принадлежат корни и

Ответ: А) Б)

Содержание критериев оценивания задачи С2	Баллы
Обоснованно получен верный ответ.	2
Верно описана геометрическая конфигурация, построен или описан геометрический объект, который нужно найти, но получен неверный ответ или решение не закончено.	1
Все прочие случаи.	0

Дана правильная треугольная пирамида DABC с вершиной D. Боковое ребро пирамиды равно , высота равна . Найдите расстояние от середины бокового ребра BD до прямой МТ, где точки М и Т — середины ребер АС и AВ соответственно.