B1	3000
B2	4
B3	5
B4	1840
B5	1
B6	8
B7	150
B8	8
B9	17
B10	0,6
B11	5
B12	2,5
B13	240
B14	5

Решения

Задание 1

Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены? Решение. Цена чайника после повышения стала составлять 116% от начальной цены. Разделим 3480 на 1,16:

. Значит, цена чайника до повышения составляла 3000 рублей.

Ответ: 3000.

Задание 2

На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода не выпадало осадков.

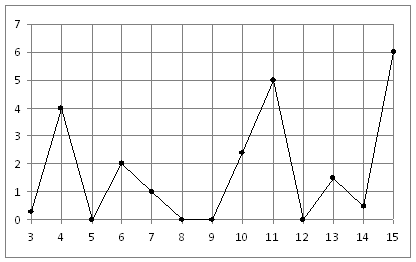Решение. Из графика видно, что 4 дня из данного периода не выпадало осадков (см. рисунок).

Ответ: 4.

Задание 3

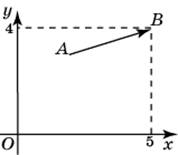Вектор  с концом в точке (5; 4) имеет координаты (3; 1). Найдите сумму координат точки . Решение. Координаты вектора равны разности координат конца вектора и его начала. Координаты точки A вычисляются следующим образом: 5 − x = 3, 4 − y = 1. Откуда x = 2, y = 3. Поэтому сумма координат точки A равна 5.

Ответ: 5.

Задание 4

Для остекления музейных витрин требуется заказать 20 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25  . В таблице приведены цены на стекло и на резку стекол. Сколько рублей будет стоить самый дешевый заказ?

Фирма	Цена стекла (руб. за 1 м2)	Резка стекла (руб. за одно стекло)	Дополнительные условия
A	300	17
Б	320	13
В	340	8	При заказе на сумму больше 2500 руб. резка бесплатно.

Решение. Общая площадь стекла, которого нужно изготовить равна 20   0,25 = 5  . Стоимость заказа в фирме А складывается из стоимости стекла 300   5 = 1500 руб. и стоимости его резки и шлифовки 17   20 = 340 руб. и равна 1840 руб. Стоимость заказа в фирме Б складывается из стоимости стекла 320   5 = 1600 руб. и стоимости его резки и шлифовки 13   20 = 260 руб. и равна 1860 руб. Стоимость заказа в фирме В складывается из стоимости стекла 340   5 = 1700 руб. и стоимости его резки и шлифовки 8   20 = 160 руб. и равна 1860 руб.

Ответ: 1840.

Задание 5

Найдите корень уравнения: . Решение.

Ответ: 1.

Задание 6

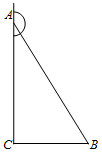В треугольнике угол равен , синус внешнего угла при вершине равен 0,5, . Найдите . Решение. так как

Ответ: 8.

Задание 7

Найдите значение выражения при . Решение.

.

Ответ: 150.

Задание 8

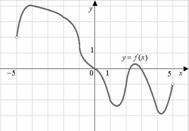На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции  отрицательна.

Решение. Производная функции отрицательна на тех интервалах, на которых функция убывает, т. е. на интервалах (−4,1; 1,5) и (2,6; 4,2). В них содержатся целые точки −4, −3, −2, −1, 0, 1, 3, 4. Их 8 штук.

Ответ: 8.

Задание 9

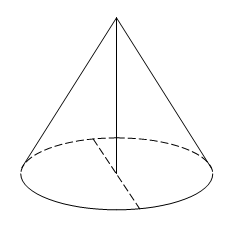Высота конуса равна 15, а диаметр основания – 16. Найдите образующую конуса. Решение. образующая конуса по теореме Пифагора равна

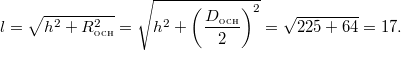
Ответ: 17.

Задание 10

В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам. Решение. Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна

Ответ: 0,6.

Задание 11

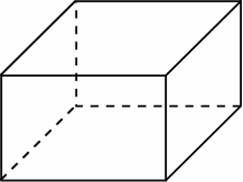Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Решение. Обозначим известные ребра за и , а неизвестное за . Площадь поверхности параллелепипеда выражается как . Выразим : , откуда неизвестное ребро

.

Ответ: 5.

Задание 12

Опорные башмаки шагающего экскаватора, имеющего массу тонн представляют собой две пустотелые балки длиной метров и шириной метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой , где – масса экскаватора (в тоннах), – длина балок в метрах, – ширина балок в метрах, – ускорение свободного падения (считайте м/с ). Определите наименьшую возможную ширину опорных балок, если известно, что давление не должно превышать 140 кПа. Ответ выразите в метрах. Решение. Задача сводится к решению неравенства кПа при известных значениях длины балок м, массы экскаватора т:

м.

Ответ: 2,5.

Задание 13

Расстояние между городами и равно 435 км. Из города в город со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города автомобили встретятся? Ответ дайте в километрах. Решение. Пусть автомобили встретятся на расстоянии км от города , тогда второй автомобиль пройдет расстояние км. Второй автомобиль находился в пути на 1 час меньше первого, отсюда имеем:

.

Ответ: 240.

Задание 14

Найдите наибольшее значение функции на отрезке . Решение. Найдём производную заданной функции: Уравнение не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей. Следовательно, наибольшим значением функции на заданном отрезке является

Ответ: 5.

Проверка части С

Начало формы

Содержание критериев оценивания задачи С1	Баллы
Обоснованно получен верный ответ.	2
Решение не содержит логических пробелов, получен ответ, неверный, но только из-за вычислительной ошибки или описки.	1
Все прочие случаи.	0

А) Решите уравнение Б) Укажите корни уравнения, принадлежащие отрезку

Решение.

А) Преобразуем уравнение:

Значит, или где В первом случае во втором случае где Первая серия решений входит во вторую. 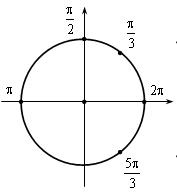Б) Отметим решения на тригонометрической окружности. Отрезку принадлежат корни и

Ответ: А) Б)

Содержание критериев оценивания задачи С2	Баллы
Обоснованно получен верный ответ.	2
Верно описана геометрическая конфигурация, построен или описан геометрический объект, который нужно найти, но получен неверный ответ или решение не закончено.	1
Все прочие случаи.	0

В правильной треугольной пирамиде с основанием точка — середина ребра точка — середина ребра Найдите угол между плоскостями и если

Решение.

Проведем перпендикуляр к — середина Из точки опустим перпендикуляр на плоскость основания. Точка лежит на медиане треугольника Прямая параллельна прямой пересечения плоскостей и и Следовательно, — линейный угол искомого угла между плоскостями. Далее находим:

Откуда

Ответ:

Содержание критериев оценивания задачи С3	Баллы
Обоснованно получен верный ответ.	3
При верной последовательности рассуждений получен ответ, неверный только из-за вычислительной ошибки или описки.	2
Получен ответ, отличающийся от верного только конечным числом точек.	1
Все прочие случаи.	0

Решите систему

Решение.

1.Решим первое неравенство:

2. Решим второе неравенство. Заметим, что при всех При условиях и получаем неравенство

При указанных условиях получаем: или 3. Решением системы является общая часть решений двух неравенств. поэтому Следовательно, или Ответ:

Содержание критериев оценивания задачи С4	Баллы
Обоснованно получен верный ответ.	3
Рассмотрены все возможные геометрические конфигурации. В одном из случаев обоснованно получен верный ответ.	2
Рассмотрены только одна из возможных геометрических конфигураций. Для нее обоснованно получен верный ответ.	1
Все прочие случаи.	0

Четырехугольник KLMP описан около окружности и вписан В окружность. Прямые KL и NM пересекаются в точке P. Найдите площадь треугольника KPN, если известно, что и радиусы окружностей, вписанных в треугольники KPN и LMP равны соответственно r и R.

Решение.

Лучи KL и NM пересекаются в точке P (см. рисунок).

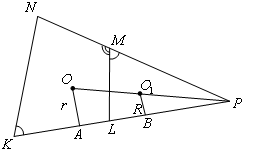
Центры и О окружностей, вписанных в треугольники KPN и LMP соответственно, лежат на биссектрисе МО угла KPN. Окружность, вписанная в четырехугольник KLMP, является также окружностью, вписанной в треугольник KPN и вневписанной окружностью треугольника LMP. Четырехугольник KLMP вписан в окружность, следовательно . Но , откуда . Так как треугольники KPN и LMP имеют еще общий угол KPN, они подобны, причем коэффициент подобия равен отношению радиусов окружностей, вписанных в эти треугольники. Далее имеем: 1) (*); 2) , где p — полупериметр треугольника LPM равный длине отрезка AP; 3) из прямоугольного треугольника ОAP находим , откуда . Подставляя найденное в формулу (*), окончательно получаем

.

Ответ: .

Содержание критериев оценивания задачи С5	Баллы
Обоснованно получен верный ответ.	4
Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку.	3
Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки.	2
Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок.	1
Все прочие случаи.	0

Найдите все положительные значения а, при каждом из которых система имеет единственное решение.