4.3. Числення висловлень.
4.3.1. Аксіоматичні теорії.
Розглянутий нами підхід до логіки висловлень заснований на законах булевої алгебри. Істинність будь-якої формули можна перевірити за допомогою таблиць істинності. Таблиці істинності дають можливість відповісти на багато питань, які стосуються формул алгебри висловлень, наприклад про рівносильність двох формул. Однак більш складні питання логіки висловлень вже не можуть бути вирішені за допомогою алгебри логіки, тобто таблиць істинності. Для вирішення цих проблем використовується інший спосіб опису висловлень – аксіоматичний, при якому використовуються аксіоматичні теорії.
Аксіоматичні
теорії – це формальні системи, які
відповідають численню висловлень. Як
і кожні формальні системи, аксіоматичні
теорії містять
алфавіт, систему аксіом, правила
виведення. Аксіоматична
теорія
будується таким чином:
- визначається набір символів теорії , тобто скінченних послідовностей, які називаються виразами теорії ;
- визначається множина формул, тобто підмножин виразів теорії ;
- визначається підмножина множини формул, які називаються аксіомами теорії ;
-
задається множина
відношень
між формулами, які називаються правилами
виведення.
Нагадаємо поняття тавтологій, здійснених формул і протиріччя.
Формула називається тавтологією (або тотожно істинною), якщо вона істина при будь-яких значеннях змінних, що входять у неї.
Формула F називається здійсненною, якщо вона істина при деяких значеннях істинності її змінних.
Формула F називається тотожно хибною (або протиріччям), якщо вона хибна при будь–яких значеннях її змінних.
Приклад
4.20.
має значення істина при будь-яких
значеннях істинності
.
Це тавтологія (тотожно істина формула).
хибна
при істинному
й хибному
,
при інших значеннях
і
формула
має істинне значення. Ця формула є
здійсненною.
має
хибне значення при будь-яких значеннях
.
Це протиріччя або тотожно хибна формула.
Приведемо твердження, які є очевидними наслідками даних тверджень:
1) – тавтологія тоді й тільки тоді, коли протиріччя.
2) протиріччя тоді й тільки тоді, коли – тавтологія.
3) – тавтологія тоді й тільки тоді, коли и рівносильні.
З погляду логічних міркувань тавтології є не що інше, як логічні закони, тому що при будь–якій підстановці замість змінних тавтології конкретних висловлень у результаті одержимо істинні висловлення. Перелічимо найбільш важливі тавтології:
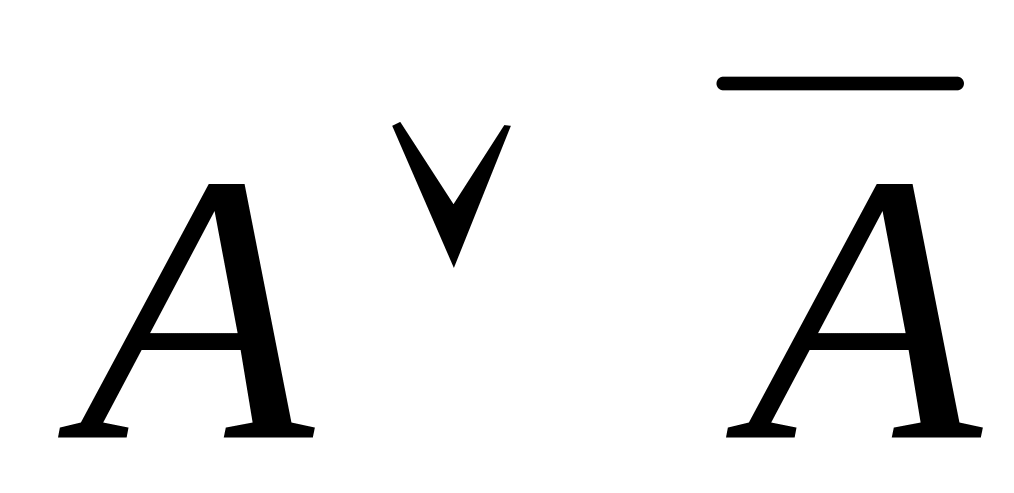(tertium
nondatur),
або закон виключного третього;
;
;
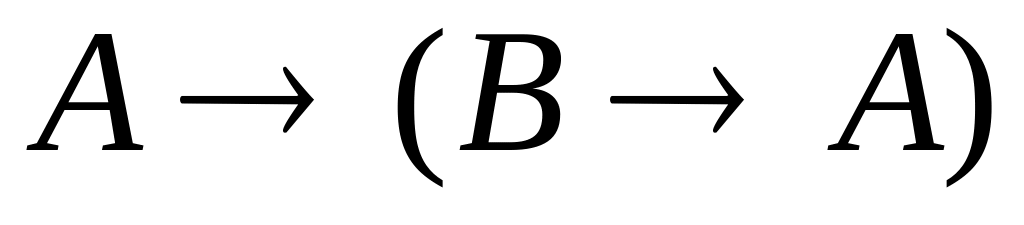(ланцюгове
міркування);
;
;
;
;
;
;
;
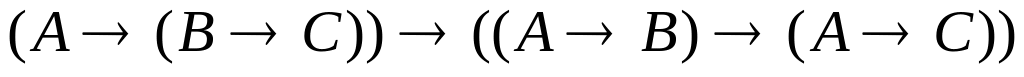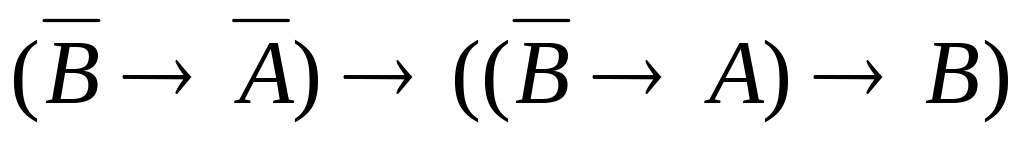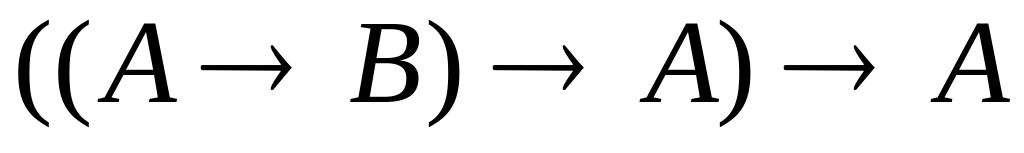(Закон
Пірса).
Кожна з цих тавтологій є аксіомою логіки висловлень.
Кожну із цих тавтологій можна довести за допомогою таблиць істинності. Наприклад доведемо №3 (табл.4.10), №5 (табл.4.11), №9 (табл.4.12)
Таблиця 4.10 |
||||
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Таблиця 4.11 |
||||||||
|
|
|
f1
|
f4
|
f2
|
f3
|
f5
|
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Таблиця 4.12 |
||||
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
