
- •Множества, функции, отношения. Операции над множествами. Соответствия и их свойства. Общее понятие отношения. Бинарные отношения и их свойства. Отношение порядка.
- •Свойства операций над множеством:
- •Бинарные отношения и их свойства.
- •2. Комбинаторика: предмет и задачи. Размещения, перестановки, сочетания без повторений и с повторениями. Биномиальные коэффициенты и соотношения для них. Комбинаторика: предмет и задачи.
- •Число сочетаний с повторениями:
- •Гомоморфизм.
Гомоморфизм.
Гомоморфизм отличается от изоморфизма тем, что соответствие объектов (систем) однозначно лишь в одну сторону. Поэтому гомоморфный образ есть неполное, приближенное отображение структуры оригинала.
Пример.
Картина и местность, грамзаписью и ее
оригинал
DEF
Если
А и В – алгебры сигнатуры
,
то отображение
 называется
гомоморфизмом,
если для всякой 0-арной операции
называется
гомоморфизмом,
если для всякой 0-арной операции
 А при
А при
 для
любой n-арной
операции
для
любой n-арной
операции
 и любых
и любых
 .
Основные
алгебраические структуры.DEF
Кольцо —
это множество R,
на котором заданы две бинарные
операции:
+ и × (называемые сложение и умножение),
со следующими свойствами:
.
Основные
алгебраические структуры.DEF
Кольцо —
это множество R,
на котором заданы две бинарные
операции:
+ и × (называемые сложение и умножение),
со следующими свойствами:
 — коммутативность сложения;
— коммутативность сложения; — ассоциативность сложения;
— ассоциативность сложения; —
существование
нейтрального элемента относительно
сложения;
—
существование
нейтрального элемента относительно
сложения; —
существование
обратного элемента относительно
сложения;
—
существование
обратного элемента относительно
сложения; —
ассоциативность
умножения (некоторые авторы не требуют
выполнения этой аксиомы)
—
ассоциативность
умножения (некоторые авторы не требуют
выполнения этой аксиомы) — дистрибутивность.
— дистрибутивность.
Пример
{0} — тривиальное кольцо, состоящее из одного нуля. Это единственное кольцо, в котором ноль является мультипликативной единицей.
![]() — целые
числа (с
обычным сложением и умножением).
— целые
числа (с
обычным сложением и умножением).
![]() —
кольцо многочленов от n переменных
над полем
—
кольцо многочленов от n переменных
над полем ![]() .
.
![]() —
кольцо вычетов по
модулю натурального числа n.
—
кольцо вычетов по
модулю натурального числа n.
![]() —
кольцо рациональных
чисел,
являющееся полем.
—
кольцо рациональных
чисел,
являющееся полем.
— кольцо вещественных чисел, являющееся полем.
По́лем называется множество F с
двумя бинарными
операциями + (аддитивная
операция,
или сложение)
и ![]() (мультипликативная
операция,
или умножение),
если оно (вместе с этими операциями)
образует коммутативное ассоциативное кольцо c
единицей
(мультипликативная
операция,
или умножение),
если оно (вместе с этими операциями)
образует коммутативное ассоциативное кольцо c
единицей ![]() ,
все ненулевые элементы
которого обратимыDEF
Полугруппа
– это алгебра с одной ассоциативной
бинарной операцией (абстрактное
умножение).Полугруппа с единичным
элементом называется моноидом.
,
все ненулевые элементы
которого обратимыDEF
Полугруппа
– это алгебра с одной ассоциативной
бинарной операцией (абстрактное
умножение).Полугруппа с единичным
элементом называется моноидом.
DEF
Группа
– это моноид и

– это
полугруппа с e
– это алгебра с ассоциативной
операцией, с е, с

DEF
Решетка
 - отношение порядка. Так что : 1)множество
М частично упорядочено 2) наибольшая
нижняя грань и наименьшая верхняя грани
единственны DEF2
Решётка, структура — частично
упорядоченное множество,
в котором каждое двухэлементное
подмножество имеет как точную верхнюю
(sup), так и точную нижнюю (inf) грани. Пример
: множество
всех подмножеств данного
множества, упорядоченное по включению;
- отношение порядка. Так что : 1)множество
М частично упорядочено 2) наибольшая
нижняя грань и наименьшая верхняя грани
единственны DEF2
Решётка, структура — частично
упорядоченное множество,
в котором каждое двухэлементное
подмножество имеет как точную верхнюю
(sup), так и точную нижнюю (inf) грани. Пример
: множество
всех подмножеств данного
множества, упорядоченное по включению;
4.
Особую роль играет
двухэлементное множество В и двоичные
переменные, принимающие значения из В.
будем считать, что В={0, 1}, рассматривая
0 и 1 как формальные символы, не имеющие
арифметического смысла. Алгебра,
образованная множеством В вместе со
всеми возможными операциями на нем,
называется алгеброй
логики.
Функцией
алгебры логики
(или логической функцией) от n
переменных называется n-арная
операция на В. Логическая функция
f(x1,...,хn)
—это функция, принимающая значения 0,
1. Множество всех логических функций
обозначается
 множество всех логических функций n
переменных —
множество всех логических функций n
переменных — .Алгебра,
образованная k-элементным
множеством вместе со всеми операциями
на нем, называется алгеброй
k-значной
логики, а
n-арные
операции на k-элементном
множестве называются k-значными
логическими функциями n
переменных;
множество всех n-значных
логических функций обозначается Рк.
.Алгебра,
образованная k-элементным
множеством вместе со всеми операциями
на нем, называется алгеброй
k-значной
логики, а
n-арные
операции на k-элементном
множестве называются k-значными
логическими функциями n
переменных;
множество всех n-значных
логических функций обозначается Рк.
В сякая
логическая функция n
переменных может быть задана таблицей,
в левой части которой перечислены все
сякая
логическая функция n
переменных может быть задана таблицей,
в левой части которой перечислены все
 наборов значений переменных (т. е.
двоичных векторов длины n),
а в правой части — значения функции на
этих наборах. Переменная xi
в функции f(x1,…,xi,
xi+i,
..., xn)
называется несущественной (или фиктивной),
если f(x1,...,xi-1,
0,xi+1,…,
xn)=f(x1,
..., xi-1,
1, xi+1,...,
xn)
при любых значениях остальных переменных,
т. е. если изменение значения xi
в любом наборе значений x1,
..., хn
не меняет значения функции.
наборов значений переменных (т. е.
двоичных векторов длины n),
а в правой части — значения функции на
этих наборах. Переменная xi
в функции f(x1,…,xi,
xi+i,
..., xn)
называется несущественной (или фиктивной),
если f(x1,...,xi-1,
0,xi+1,…,
xn)=f(x1,
..., xi-1,
1, xi+1,...,
xn)
при любых значениях остальных переменных,
т. е. если изменение значения xi
в любом наборе значений x1,
..., хn
не меняет значения функции.

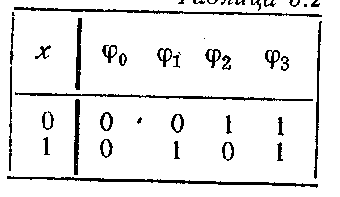 -число
логических функций от n
переменных. Функции
-число
логических функций от n
переменных. Функции
 и
и
 — константы 0 и 1 соответственно; их
значения не зависят от значения
переменной, и, следовательно, переменная
х для них несущественна. Функция
— константы 0 и 1 соответственно; их
значения не зависят от значения
переменной, и, следовательно, переменная
х для них несущественна. Функция
 «повторяет» х:
«повторяет» х:
 .
Функция
.
Функция
 называется отрицанием х (или функцией
НЕ). Логических функций двух переменных—16.
называется отрицанием х (или функцией
НЕ). Логических функций двух переменных—16.
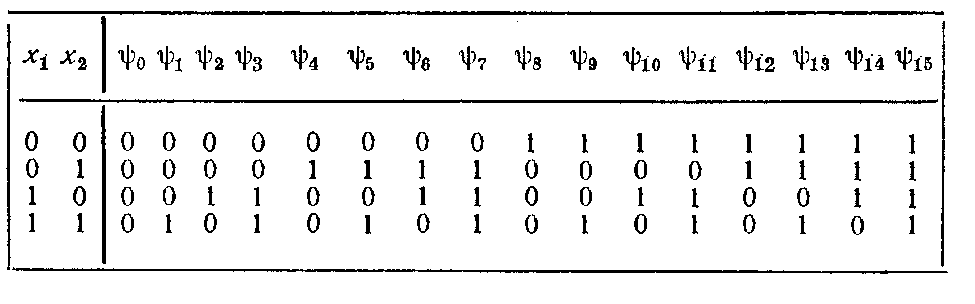 (x1,x2)-конъюнкция
(И)
(x1,x2)-конъюнкция
(И)
 -
дизъюнкция (ИЛИ)
-
дизъюнкция (ИЛИ)
 -
импликация (
-
импликация ( )
)
 -
эквивалентность
-
эквивалентность
 -
сложение по модулю 2
-
сложение по модулю 2
 ,
,
 -стрелка
Пирса
-стрелка
Пирса
 ,
,
 -
штрих Шеффера
-
штрих Шеффера Функция может быть задана таблицей
или логической формулой. Формулы
эквивалентны, если они представляют
одну и ту же функцию (на любом наборе
переменных из значения совпадают).Если
любую логическую формулу можно выразить
через суперпозицию данных функцию,
такую систему называют функционально
полной (сильно функционально полной).Система
функционально
полна в слабом смысле,
если при добавлении с этой системе 2х
констант 0 и 1 она становится ф.п. в сильном
смысле. Пусть
Функция может быть задана таблицей
или логической формулой. Формулы
эквивалентны, если они представляют
одну и ту же функцию (на любом наборе
переменных из значения совпадают).Если
любую логическую формулу можно выразить
через суперпозицию данных функцию,
такую систему называют функционально
полной (сильно функционально полной).Система
функционально
полна в слабом смысле,
если при добавлении с этой системе 2х
констант 0 и 1 она становится ф.п. в сильном
смысле. Пусть
 —параметр,
равный 0 или 1. Тогда
—параметр,
равный 0 или 1. Тогда
 ,
если х=а, и
,
если х=а, и
 ,
если х!=а. Теорема:
Всякая логическая функция f(x1,...,xn)
может быть представлена в следующем
виде:
,
если х!=а. Теорема:
Всякая логическая функция f(x1,...,xn)
может быть представлена в следующем
виде: ,
где m<=n,
а дизъюнкция берется по всем 2m
наборам значений переменных х1, ..., хm.Это
равенство называется разложением
по переменным
x1,
..., хm.
Важный случай — разложение по всем n
переменным. При этом все переменные в
правой части получают фиксированные
значения и функции в конъюнкциях правой
части становятся равными 0 или 1, что
дает:
,
где m<=n,
а дизъюнкция берется по всем 2m
наборам значений переменных х1, ..., хm.Это
равенство называется разложением
по переменным
x1,
..., хm.
Важный случай — разложение по всем n
переменным. При этом все переменные в
правой части получают фиксированные
значения и функции в конъюнкциях правой
части становятся равными 0 или 1, что
дает:
 ,
где дизъюнкция берется по всем наборам
(
,
где дизъюнкция берется по всем наборам
( ),
на которых f=1.
Такое разложение называется совершенной
дизъюнктивной нормальной формой
(СДНФ) функции f.
СДНФ функции f
содержит ровно столько конъюнкций,
сколько единиц в таблице f;
каждому единичному набору (
)
соответствует конъюнкция всех переменных,
в которой xi
взято с отрицанием, если
),
на которых f=1.
Такое разложение называется совершенной
дизъюнктивной нормальной формой
(СДНФ) функции f.
СДНФ функции f
содержит ровно столько конъюнкций,
сколько единиц в таблице f;
каждому единичному набору (
)
соответствует конъюнкция всех переменных,
в которой xi
взято с отрицанием, если
 = 0, и без отрицания, если
= l.
Таким образом, существует взаимно
однозначное соответствие между таблицей
функции f(x1,
...,xn)
и ее СДНФ, и, следовательно, СДНФ для
всякой логической функции
единственна.Единственная функция, не
имеющая СДНФ, — это константа 0. Формулы,
содержащие, кроме переменных (и скобок),
только знаки функций дизъюнкции,
конъюнкции и отрицания, будем называть
булевыми
формулами
(знак конъюнкции может опускаться).
Теорема:
Всякая логическая функция может быть
представлена булевой формулой, т. е. как
суперпозиция конъюнкции, дизъюнкции и
отрицания. Действительно, для всякой
функции, кроме константы 0, таким
представлением может служить ее СДНФ.
Константу 0 можно представить булевой
формулой
= 0, и без отрицания, если
= l.
Таким образом, существует взаимно
однозначное соответствие между таблицей
функции f(x1,
...,xn)
и ее СДНФ, и, следовательно, СДНФ для
всякой логической функции
единственна.Единственная функция, не
имеющая СДНФ, — это константа 0. Формулы,
содержащие, кроме переменных (и скобок),
только знаки функций дизъюнкции,
конъюнкции и отрицания, будем называть
булевыми
формулами
(знак конъюнкции может опускаться).
Теорема:
Всякая логическая функция может быть
представлена булевой формулой, т. е. как
суперпозиция конъюнкции, дизъюнкции и
отрицания. Действительно, для всякой
функции, кроме константы 0, таким
представлением может служить ее СДНФ.
Константу 0 можно представить булевой
формулой
 .Дизъюнкцию
можно раcсматривать
как бинарную операцию на множестве
логических функций, которая каждой паре
функций fi,
f2
независимо от вида формул, которыми они
представлены, однозначно ставит в
соответствие функцию f1Vf2.
Аналогично этому можно рассматривать
конъюнкцию как бинарную операцию, а
отрицание—как унарную операцию над
функциями. Алгебра (Р2,V,
&, ¬), основным множеством которой
является все множество логических
функций, а операциями— дизъюнкция,
конъюнкция и отрицание, называется
булевой
алгеброй логических функций.
Операции булевой алгебры также часто
называют булевыми операциями. Свойства
булевых функций:
ассоциативность, коммутативность,
дистрибутивность дизъюнкции относительно
конъюнкции и наоборот, двойное отрицание,
идемпотентность (
.Дизъюнкцию
можно раcсматривать
как бинарную операцию на множестве
логических функций, которая каждой паре
функций fi,
f2
независимо от вида формул, которыми они
представлены, однозначно ставит в
соответствие функцию f1Vf2.
Аналогично этому можно рассматривать
конъюнкцию как бинарную операцию, а
отрицание—как унарную операцию над
функциями. Алгебра (Р2,V,
&, ¬), основным множеством которой
является все множество логических
функций, а операциями— дизъюнкция,
конъюнкция и отрицание, называется
булевой
алгеброй логических функций.
Операции булевой алгебры также часто
называют булевыми операциями. Свойства
булевых функций:
ассоциативность, коммутативность,
дистрибутивность дизъюнкции относительно
конъюнкции и наоборот, двойное отрицание,
идемпотентность ( ),
правила де Моргана (
),
правила де Моргана ( ,
и наоборот), закон противоречия (
=0)
и исключенного третьего (
,
и наоборот), закон противоречия (
=0)
и исключенного третьего ( ).
Теорема (о
функциональной полноте):
система функций является функционально
полной в слабом смысле тогда и только
тогда, когда она содержит хотя бы одну
немонотонную и хотя бы одну не линейную
функции5Теорию
графов начали разрабатывать для решения
некоторых задач о геометрических
конфигурациях, состоящих из точек и
линий. В этих задачах несущественно,
соединены ли точки отрезками или дугами,
какова длина линий и другие геометр
характеристики. Важно лишь то, что каждая
линия соединяет какие-либо две из
заданных точек. Опр:
граф – совокупность двух множеств V
(точек) и Е (линий), между элементами
которых определено отношение
инцидентности, причем каждый элемент
).
Теорема (о
функциональной полноте):
система функций является функционально
полной в слабом смысле тогда и только
тогда, когда она содержит хотя бы одну
немонотонную и хотя бы одну не линейную
функции5Теорию
графов начали разрабатывать для решения
некоторых задач о геометрических
конфигурациях, состоящих из точек и
линий. В этих задачах несущественно,
соединены ли точки отрезками или дугами,
какова длина линий и другие геометр
характеристики. Важно лишь то, что каждая
линия соединяет какие-либо две из
заданных точек. Опр:
граф – совокупность двух множеств V
(точек) и Е (линий), между элементами
которых определено отношение
инцидентности, причем каждый элемент
 инцидентен ровно двум элементам
инцидентен ровно двум элементам
 .
Элементы множества V называются вершинами
графа G, элементы множества Е — его
ребрами.
В некоторых задач инцидентные ребру
вершины неравноправны, они рассматриваются
в определенном порядке. Тогда каждому
ребру можно приписать направление от
первой из инцидентных вершин ко второй.
Направленные ребра называют дугами,
а содержащий их граф — ориентированным
(граф, определенный ранее, называется
неориентированным). Первая по порядку
вершина, инцидентная ребру ориентированного
графа, называется его началом, вторая
— его концом. Множество ребер мобыть
пустым. Если же множество вершин V пусто,
то пусто и Е. Такой граф называется
пустым.
Линии, изображаю ребра графа, могут
пересекаться, но точки пересечения не
являются вершинами; различные ребра
могут быть инцидентны одной и той же
паре вершин, в этом случае они называются
кратными;
граф, содержащий кратные ребра, часто
называют мультиграфом.
Ребро может соединять некоторую вершину
саму с собой, такое ребро называется
петлей.
Обычно рассматриваемые графы конечны,
т. е. конечны множества их элементов
(вершин и ребер), но могут быть и
бесконечными.При изображении
ориентированных графов направления
ребер отмечаются стрелками, примыкающими
к их концам. Ориентированный граф также
может иметь кратные ребра, петли, а также
соединяющие одни и те же вершины ребра,
идущие в противоположных направлениях.Каждому
неориентированному графу можно поставить
в соответствие ориентированный граф с
тем же множеством вершин, в котором
каждое ребро заменено двумя ориентированными
ребрами, инцидентными тем же вершинам
и имеющими противоположные направления.
Такое соответствие будем называть
каноническим. Матрица
инцидентности и список ребер.
Задать граф —описать множества его
вершин и ребер, а также отношение
инцидентности. Когда граф G — конечный,
для описания его вершин и ребер достаточно
их занумеровать. Пусть
.
Элементы множества V называются вершинами
графа G, элементы множества Е — его
ребрами.
В некоторых задач инцидентные ребру
вершины неравноправны, они рассматриваются
в определенном порядке. Тогда каждому
ребру можно приписать направление от
первой из инцидентных вершин ко второй.
Направленные ребра называют дугами,
а содержащий их граф — ориентированным
(граф, определенный ранее, называется
неориентированным). Первая по порядку
вершина, инцидентная ребру ориентированного
графа, называется его началом, вторая
— его концом. Множество ребер мобыть
пустым. Если же множество вершин V пусто,
то пусто и Е. Такой граф называется
пустым.
Линии, изображаю ребра графа, могут
пересекаться, но точки пересечения не
являются вершинами; различные ребра
могут быть инцидентны одной и той же
паре вершин, в этом случае они называются
кратными;
граф, содержащий кратные ребра, часто
называют мультиграфом.
Ребро может соединять некоторую вершину
саму с собой, такое ребро называется
петлей.
Обычно рассматриваемые графы конечны,
т. е. конечны множества их элементов
(вершин и ребер), но могут быть и
бесконечными.При изображении
ориентированных графов направления
ребер отмечаются стрелками, примыкающими
к их концам. Ориентированный граф также
может иметь кратные ребра, петли, а также
соединяющие одни и те же вершины ребра,
идущие в противоположных направлениях.Каждому
неориентированному графу можно поставить
в соответствие ориентированный граф с
тем же множеством вершин, в котором
каждое ребро заменено двумя ориентированными
ребрами, инцидентными тем же вершинам
и имеющими противоположные направления.
Такое соответствие будем называть
каноническим. Матрица
инцидентности и список ребер.
Задать граф —описать множества его
вершин и ребер, а также отношение
инцидентности. Когда граф G — конечный,
для описания его вершин и ребер достаточно
их занумеровать. Пусть
 — вершины графа G; е1, е2, ..., еm
— его ребра. Отношение инцидентности
можно определить матрицей
— вершины графа G; е1, е2, ..., еm
— его ребра. Отношение инцидентности
можно определить матрицей
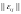 ,
имеющей m
строк и n
столбцов. Столбцы соответствуют вершинам
графа, строки — ребрам. Если ребро ei
инцидентно вершине vj,
то
,
имеющей m
строк и n
столбцов. Столбцы соответствуют вершинам
графа, строки — ребрам. Если ребро ei
инцидентно вершине vj,
то
 ,
в противном случае
,
в противном случае
 .
Это так называемая матрица
инцидентности
неориентированного графа G, которая
является одним из способов его
определения.В матрице инцидентности
ориентированного графа G, если вершина
vj
— начало ребра ai,
то
.
Это так называемая матрица
инцидентности
неориентированного графа G, которая
является одним из способов его
определения.В матрице инцидентности
ориентированного графа G, если вершина
vj
— начало ребра ai,
то
 ;
если — конец, то =1; если аi
— петля, а vj
— инцидентная ей вершина, то
;
если — конец, то =1; если аi
— петля, а vj
— инцидентная ей вершина, то
 ,
где альфа — любое число, отличное от 1,
0 и —1, в остальных случаях
В каждой строке матрицы инцидентности
для неориентированного или ориентированного
графа только два элемента отличны от 0
(или один, если ребро является петлей).
Поэтому такой способ задания графа
оказывается недостаточно экономным.
Отношение инцидентности можно задать
списком ребер графа. Каждая строка этого
списка соответствует ребру, в ней
записаны номера вершин, инцидентных
ему. Для неориентированного графа
порядок этих вершин в строке произволен,
для ориентированного первым стоит номер
или другое наименование начала ребра,
а вторым — его конца. По списку ребер
графа легко построить его матрицу
инцидентности.. Для неориентированного
графа в строке списка указаны номера
элементов строки матрицы инцидентности,
равные 1, и для ориентированного графа
в этой строке первым стоит номер элемента
строки матрицы, равного—1, а вторым —
номер элемента, равного + 1. Матрица
смежности графа.
Это квадратн матрица
,
где альфа — любое число, отличное от 1,
0 и —1, в остальных случаях
В каждой строке матрицы инцидентности
для неориентированного или ориентированного
графа только два элемента отличны от 0
(или один, если ребро является петлей).
Поэтому такой способ задания графа
оказывается недостаточно экономным.
Отношение инцидентности можно задать
списком ребер графа. Каждая строка этого
списка соответствует ребру, в ней
записаны номера вершин, инцидентных
ему. Для неориентированного графа
порядок этих вершин в строке произволен,
для ориентированного первым стоит номер
или другое наименование начала ребра,
а вторым — его конца. По списку ребер
графа легко построить его матрицу
инцидентности.. Для неориентированного
графа в строке списка указаны номера
элементов строки матрицы инцидентности,
равные 1, и для ориентированного графа
в этой строке первым стоит номер элемента
строки матрицы, равного—1, а вторым —
номер элемента, равного + 1. Матрица
смежности графа.
Это квадратн матрица
 ,
столбцам и строкам которой соответствуют
вершины графа. Для неориентированного
графа
,
столбцам и строкам которой соответствуют
вершины графа. Для неориентированного
графа
 равно количеству ребер, инцидентных
i-й и j-й
вершинам, для ориентированного графа
этот элемент матрицы смежности равен
количеству ребер с началом в i-й
вершине и концом в j-й.
Таким образом, матрица смежности
неориентированного графа симметрична
(
равно количеству ребер, инцидентных
i-й и j-й
вершинам, для ориентированного графа
этот элемент матрицы смежности равен
количеству ребер с началом в i-й
вершине и концом в j-й.
Таким образом, матрица смежности
неориентированного графа симметрична
( ),
а ориентированного – необязательно.
Матрица смежности также определяет
соответствующий неориентированный или
ориентированный граф. Число его вершин
равно размерности матрицы n,
i-й
и j-й
вершинам графа инцидентны
ребер. Для неориентированного графа
и
все его ребра определяются верхним
правым треугольником матрицы, расположенным
над диагональю, включая последнюю. В
обоих случаях по матрице смежности
легко строится, например, список ребер,
определяющий граф. Элементу матрицы
смежности, расположенному в i-й
строке и j-м
столбце, соответствуют
строк списка ребер,в каждой из которых
записаны номера i, j.
Для неориентированного графа эти строки
соответствуют только элементам
описанного ранее верхнего правого
треугольника матрицы смежности, т. е.
элементам 6о с j>=i, а для ориентированного
графа нужно рассматривать все элементы
.Граф
может быть представлен различными
способами. Он может быть изображен на
чертеже, задан матрицей инцидентности,
списком ребер или матрицей смежности.
Вид чертежа зависит от формы линий и
взаимного расположения вершин. Граф
считается полностью заданным, если
нумерация его вершин зафиксирована;
графы, отличающиеся только нумерацией
вершин, называются изоморфными.Количество
p(v) ребер, инцидентных вершине v,
называется ее локальной
степенью или
просто степенью.
Для вершин ориентированного графа
определяются две локальные степени:
p1(v)
—число ребер с началом в вершине v, или,
иначе, количество выходящих из v ребер,
и р2(v)
—количество входящих в v ребер, для
которых эта вершина является концом.Граф
H
называется частью
графа G,
если множество его вершин V(H)
содержится в множестве V(G),
а множество Е(Н) ребер — в E(G).
Если V(Н)
=V(G),
часть графа называется суграфом.
Подграфом
G(U)
графа G
с множеством вершин U
),
а ориентированного – необязательно.
Матрица смежности также определяет
соответствующий неориентированный или
ориентированный граф. Число его вершин
равно размерности матрицы n,
i-й
и j-й
вершинам графа инцидентны
ребер. Для неориентированного графа
и
все его ребра определяются верхним
правым треугольником матрицы, расположенным
над диагональю, включая последнюю. В
обоих случаях по матрице смежности
легко строится, например, список ребер,
определяющий граф. Элементу матрицы
смежности, расположенному в i-й
строке и j-м
столбце, соответствуют
строк списка ребер,в каждой из которых
записаны номера i, j.
Для неориентированного графа эти строки
соответствуют только элементам
описанного ранее верхнего правого
треугольника матрицы смежности, т. е.
элементам 6о с j>=i, а для ориентированного
графа нужно рассматривать все элементы
.Граф
может быть представлен различными
способами. Он может быть изображен на
чертеже, задан матрицей инцидентности,
списком ребер или матрицей смежности.
Вид чертежа зависит от формы линий и
взаимного расположения вершин. Граф
считается полностью заданным, если
нумерация его вершин зафиксирована;
графы, отличающиеся только нумерацией
вершин, называются изоморфными.Количество
p(v) ребер, инцидентных вершине v,
называется ее локальной
степенью или
просто степенью.
Для вершин ориентированного графа
определяются две локальные степени:
p1(v)
—число ребер с началом в вершине v, или,
иначе, количество выходящих из v ребер,
и р2(v)
—количество входящих в v ребер, для
которых эта вершина является концом.Граф
H
называется частью
графа G,
если множество его вершин V(H)
содержится в множестве V(G),
а множество Е(Н) ребер — в E(G).
Если V(Н)
=V(G),
часть графа называется суграфом.
Подграфом
G(U)
графа G
с множеством вершин U V
называется часть, которой принадлежат
все ребра с обоими концами из U.
Клика
– полный подграф.Маршрутом(путем)
в G называется такая конечная или бескон
последовательность ребер, что каждые
два соседние ребра имеют общую инцидентную
вершину. Простой
путь-не
содержит пересечений с самим собой.Маршрут
М называется цепью,
если каждое ребро встречается в нем не
более одного раза. Циклический маршрут
называют циклом,
если он является цепью. Однако фактическим
циклом считают циклически упорядоченное
множество ребер, в котором два соседних
ребра имеют общую инцидентную вершину.
Цепь наименьшей длины – расстояние
между вершинами.Вершины v', v"
называются связанными,
если существует маршрут М с началом v'
и концом v". Обычно считают, что
изолированная вершина также связана
сама с собой и отношение связанности
двух вершин, заданное на множестве
вершин графа G,
рефлексивно. Как было указано ранее,
оно симметрично. Наконец, оно транзитивно.
Итак, отношение связанности вершин
обладает свойствами отношения
эквивалентности и определяет разбиение
множества вершин графа на непересекающиеся
подмножества Vi. Вершины одного и того
же множества Vi связаны друг с другом, а
вершины различных множеств Vi
и Vj
не связаны между собой. Поэтому в графе
G нет ребер с концами в разных множествах
Vi
и Vj,
и он может быть разложен в прямую сумму
подграфов Vi.
Граф G называется связным,
если все его вершины связаны между
собой. Поэтому все подграфы G(Vi) связны
и называются связными
компонентами
рассматриваемого графа. Ориентированный
граф называется сильно-связным,
если в нем существует (ориентированный)
путь из любой вершины в любую другую.
Ориентированный граф называется
слабо-связным,
если связным является неориентированный
граф, полученный заменой ориентированных
ребер. Двусвязный
граф –
граф, в котором нет шарниров. Шарнир –
вершина, в результате удаления которой
вместе со всеми инцидентными ей ребрами
количество компонент связности в графе
не возрастает.Диаметр
графа – наибольшее расстояние между
вершинами. Максимальное
удаление
от некоторой вершины – максимальное
из расстояний от этой вершины до всех
остальных. Радиус
– минимальное из максимальных удалений.
Вершины, для которых их максимальное
удаление совпадает с радиусом графа –
центры
графа.Эйлеров
обход –
цикл в связном графе, в котором каждое
ребро содержится ровно один раз.Теорема:
в связном графе Эйлеров обход существует
тогда и только тогда, когда степени всех
вершин четны.Гамильтонов
обход –
цикл в связном графе, в котором каждая
вершина содержится ровно один
раз.Неориентированное дерево
— это связный неориентированный граф
без циклов, а значит, без петель и кратных
ребер. Несвязный (неориентированный)
граф без циклов называется лесом;
связные компоненты леса являются
деревьями. Любая часть леса или дерева
также не имеет циклов, т. е. является
лесом или деревом.Вершина v графа G
называется концевой,
или висячей
(листом),
если ее степень p(v) равна единице.
Инцидентное концевой вершине ребро
также называется концевым.
Если конечное дерево состоит более чем
из одной вершины, оно имеет хотя бы две
концевые вершины и хотя бы одно концевое
ребро.Цикломатическое
число
=m-n+k,
m-число
ребер, n-число
вершин,k-число
компонент связности. Для дерева и леса
=0, для любого другого >0.Ориентированное
дерево. Из
неориентированного дерева не всякое
введение ориентации приведет к
ориентированному дереву. Выбирается
вершина (корень), все остальные ребра
ориентируются от нее. В корень ни одно
ребро не входит, во всех остальных точно
есть одно входящее ребро. Из корня есть
ориентированный путь в любую из вершин,
и при этом только из корня. Ориентированное
дерево слабо-связно. Задача
сетевого планирования.
Анализ графа определенного вида –
ациклический граф с одним источником
и одним стоком. Предполагается, что
вершины топологически отсортированы.
Веса – время, вершины – события, ребра
– работа проекта. 1-начало проекта, N
– окончание проекта. Задачи: Выяснение
времени, за которое проект будет законен.
Ранний срок
(для вершины) E(i)–
наименьший срок, в который данное событие
может произойти. Поздний
срок L(i)–
максимальное время наступления события,
которое не задержит проект в целом
(вычисляется с конца). Пусть максимальной
длины называется критическим,
любая задержка на нем приведет к задержке
всего проекта. Чем больше критических
путей, тем проект напряженней. Виды
резервов: Полный резерв -
ПР(i,j)=L(j)-E(i)-t(i,j)
– максимальная задержка на ребре,
которая не задерживает проект в целом.
Свободный резерв СР(i,j)=E(j)-E(i)-t(i,j)Независимый
резерв НР(i,j)=E(j)-L(i)-t(i,j)ПР>=СР>=НР
Задача
Потоки в сетях.Сеть
– взвешенный граф, один источник, один
сток, не обязательно ацикличный, веса
целочисленные. Веса – пропускная
способность.Поток – функция, определенная
на ребрах (положительный и <=пропускной
способности + сумма входных потоков =
сумме выходящих (закон Кирхгофа)).Нужно
при заданной пропускной способности
назначить максимальный поток в сети.
(алгоритм – назначить минимальный и
его увеличить):6
Общее
понятие алгоритма.
Тезис Черча. Тьюринга.
Основные
требования к алгоритмам 1)
алгоритм имеет дело с данными – входными,
промежуточными и выходными.В теории
алгоритмов фиксируют конкретные конечные
наборы исходных объектов (называемых
элементарными) и конечный набор средств
построения из них других объектов. Набор
элементарных объектов образует конечный
алфавит
исходных
символов.. Слова конечной длины в конечных
алфавитах - обычный тип алгоритмических
данных, число символов в слове– единица
измерения информации. Более сложный
алгоритмический объект – формула.
2)Данные
для своего размещ требуют памяти.
Память обычно считается однородной и
дискретной, т.е. состоит из одинак ячеек,
причем каждая ячейка может содержать
один символ алфавита данных. Т о, единицы
измерения объема данных и памяти
согласованы. 3)Алгоритм
состоит из отдельных элементарных
шагов,
причем множество различных шагов, из
которых составлен алгоритм, конечно.
Типичный пример множества элементарных
действий – система команд компьютера.
Обычно элементарный шаг имеет дело с
фиксированным числом символов.4)
Последовательность шагов алгоритма
детерминирована,
т.е. после каждого шага либо указывается,
какой шаг делать дальше, либо дается
команда остановки, после чего работа
алгоритма считается законченной.5)Требование
результативности
алгоритма, т.е. алгоритм должен
останавливаться после конечного числа
шагов (зависящего от данных) с указанием
того, что считать результатом. В частности,
при предъявлении алгоритма решения
задачи, например вычисления функции
f(x), нужно показать, что алгоритм
останавливается после конечного числа
шагов (сходится)
для любого x из области задания f. В
отличие от требований 1-4, сходимость
алгоритма обычно не удается установить
простым просмотром его описания. Вообще,
не существует общего способа проверки
сходимости алгоритма.
\\Следует
различать:a)Описание
алгоритма б)Механизм
реализации включающий средства пуска,
установки, реализации элементарных
шагов, выдачи результатов и обеспечения
детерминированности, т.е. управления
ходом вычисления.в)Процесс
реализации алгоритма, т.е. последовательность
шагов, которая будет порождена при
применении алгоритма к конкретным
данны///Алгоритм можно описать с помощью
блок-схемы,
т.е. графа, в котором вершинам соответствуют
шаги, а ребрам – переходы между шагами.
Язык блок-схем очень нагляден, однако,
он достаточно груб и отражает связи
лишь по управлению (что делать в следующий
момент времени, т.е. какому блоку передать
управление), а не по информации (где
этому блоку брать исходные данные).
\\Т.о,
при построении алгоритма в теории
алгоритмов используется следующий
подход: выбирается конечный набор
исходных объектов, которые объявляются
элементарными, и конечный набор построения
из них новых объектов. Данными при этом
считаются множества слов в конечных
алфавитах. Для уточнения детерминизма
используются либо блок схемы, либо
эквивалентные им словесные описания,
либо описание механизма реализации
алгоритма. Кроме того, нужно зафиксировать
набор элементарных шагов и договориться
об организации памяти.\\Рассматриваемые
алгоритмические модели формализуют
понятие «алгоритм». Это значит, что они
должны. допускать описание любых
алгоритмов. Основные цели создания
теории алгоритмов – универсальность
и связанная с ней возможность говорить
в рамках какой-либо модели о свойствах
алгоритмов вообще. Можно выделить три
основных типа универсальных алгоритмических
моделей, различающихся исходными
эвристическими соображениями относительно
того, что такое алгоритм. Первый тип
связывает понятие алгоритма с традиционным
понятием математики – вычислениями и
числовыми функциями. Наиболее развитая
модель этого типа – рекурсивные
функции
– является первой реализацией алгоритма.
Второй основан на представлении об
алгоритме как о некотор детерминированном
устройстве, способном выполнять в каждый
момент времени весьма примитивные
операции. Основной теоретической моделью
этого типа является машина
Тьюринга,
созданная в 30-х. Третий тип– это
преобразование слов в произвольных
алфавитах, в которых элементарными
операциями являются подстановки. Примеры
моделей этого типа – канонические
системы Поста и нормальные алгоритмы
Маркова. \\Машина
Тьюрин состоит
из: 1)управляющего
устройства, которое может находиться
в одном из состояний, образующих конечное
множество Q = {q1,…,
qn}2)ленты,
разбитой на ячейки, в каждой из которых
может быть записан один из символов
конечного алфавита A = {a1,
… am}3)устройства
обращения к ленте, т.е. считывающей и
пишущей головки, которая в каждый момент
времени обозревает ячейку ленты и в
зависимости от символа в этой ячейке и
состояния управляющего устройства,
записывает в нее символ, сдвигается на
ячейку влево или вправо или остается
на месте, при этом управляющее устройство
переходит в новое состояние (или остается
в старом). Среди состояний управляющего
устройства выделены начальное состояние
q1
и заключительное qz.
Память
МТ
–конечное множество состояний (внутренняя
память) и лента (внешняя память). Лента
бесконечна в обе стороны, однако в начал
момент времени только конечное число
ячеек заполнено непустыми символами,
остальные же содержат пустой символ
V
называется часть, которой принадлежат
все ребра с обоими концами из U.
Клика
– полный подграф.Маршрутом(путем)
в G называется такая конечная или бескон
последовательность ребер, что каждые
два соседние ребра имеют общую инцидентную
вершину. Простой
путь-не
содержит пересечений с самим собой.Маршрут
М называется цепью,
если каждое ребро встречается в нем не
более одного раза. Циклический маршрут
называют циклом,
если он является цепью. Однако фактическим
циклом считают циклически упорядоченное
множество ребер, в котором два соседних
ребра имеют общую инцидентную вершину.
Цепь наименьшей длины – расстояние
между вершинами.Вершины v', v"
называются связанными,
если существует маршрут М с началом v'
и концом v". Обычно считают, что
изолированная вершина также связана
сама с собой и отношение связанности
двух вершин, заданное на множестве
вершин графа G,
рефлексивно. Как было указано ранее,
оно симметрично. Наконец, оно транзитивно.
Итак, отношение связанности вершин
обладает свойствами отношения
эквивалентности и определяет разбиение
множества вершин графа на непересекающиеся
подмножества Vi. Вершины одного и того
же множества Vi связаны друг с другом, а
вершины различных множеств Vi
и Vj
не связаны между собой. Поэтому в графе
G нет ребер с концами в разных множествах
Vi
и Vj,
и он может быть разложен в прямую сумму
подграфов Vi.
Граф G называется связным,
если все его вершины связаны между
собой. Поэтому все подграфы G(Vi) связны
и называются связными
компонентами
рассматриваемого графа. Ориентированный
граф называется сильно-связным,
если в нем существует (ориентированный)
путь из любой вершины в любую другую.
Ориентированный граф называется
слабо-связным,
если связным является неориентированный
граф, полученный заменой ориентированных
ребер. Двусвязный
граф –
граф, в котором нет шарниров. Шарнир –
вершина, в результате удаления которой
вместе со всеми инцидентными ей ребрами
количество компонент связности в графе
не возрастает.Диаметр
графа – наибольшее расстояние между
вершинами. Максимальное
удаление
от некоторой вершины – максимальное
из расстояний от этой вершины до всех
остальных. Радиус
– минимальное из максимальных удалений.
Вершины, для которых их максимальное
удаление совпадает с радиусом графа –
центры
графа.Эйлеров
обход –
цикл в связном графе, в котором каждое
ребро содержится ровно один раз.Теорема:
в связном графе Эйлеров обход существует
тогда и только тогда, когда степени всех
вершин четны.Гамильтонов
обход –
цикл в связном графе, в котором каждая
вершина содержится ровно один
раз.Неориентированное дерево
— это связный неориентированный граф
без циклов, а значит, без петель и кратных
ребер. Несвязный (неориентированный)
граф без циклов называется лесом;
связные компоненты леса являются
деревьями. Любая часть леса или дерева
также не имеет циклов, т. е. является
лесом или деревом.Вершина v графа G
называется концевой,
или висячей
(листом),
если ее степень p(v) равна единице.
Инцидентное концевой вершине ребро
также называется концевым.
Если конечное дерево состоит более чем
из одной вершины, оно имеет хотя бы две
концевые вершины и хотя бы одно концевое
ребро.Цикломатическое
число
=m-n+k,
m-число
ребер, n-число
вершин,k-число
компонент связности. Для дерева и леса
=0, для любого другого >0.Ориентированное
дерево. Из
неориентированного дерева не всякое
введение ориентации приведет к
ориентированному дереву. Выбирается
вершина (корень), все остальные ребра
ориентируются от нее. В корень ни одно
ребро не входит, во всех остальных точно
есть одно входящее ребро. Из корня есть
ориентированный путь в любую из вершин,
и при этом только из корня. Ориентированное
дерево слабо-связно. Задача
сетевого планирования.
Анализ графа определенного вида –
ациклический граф с одним источником
и одним стоком. Предполагается, что
вершины топологически отсортированы.
Веса – время, вершины – события, ребра
– работа проекта. 1-начало проекта, N
– окончание проекта. Задачи: Выяснение
времени, за которое проект будет законен.
Ранний срок
(для вершины) E(i)–
наименьший срок, в который данное событие
может произойти. Поздний
срок L(i)–
максимальное время наступления события,
которое не задержит проект в целом
(вычисляется с конца). Пусть максимальной
длины называется критическим,
любая задержка на нем приведет к задержке
всего проекта. Чем больше критических
путей, тем проект напряженней. Виды
резервов: Полный резерв -
ПР(i,j)=L(j)-E(i)-t(i,j)
– максимальная задержка на ребре,
которая не задерживает проект в целом.
Свободный резерв СР(i,j)=E(j)-E(i)-t(i,j)Независимый
резерв НР(i,j)=E(j)-L(i)-t(i,j)ПР>=СР>=НР
Задача
Потоки в сетях.Сеть
– взвешенный граф, один источник, один
сток, не обязательно ацикличный, веса
целочисленные. Веса – пропускная
способность.Поток – функция, определенная
на ребрах (положительный и <=пропускной
способности + сумма входных потоков =
сумме выходящих (закон Кирхгофа)).Нужно
при заданной пропускной способности
назначить максимальный поток в сети.
(алгоритм – назначить минимальный и
его увеличить):6
Общее
понятие алгоритма.
Тезис Черча. Тьюринга.
Основные
требования к алгоритмам 1)
алгоритм имеет дело с данными – входными,
промежуточными и выходными.В теории
алгоритмов фиксируют конкретные конечные
наборы исходных объектов (называемых
элементарными) и конечный набор средств
построения из них других объектов. Набор
элементарных объектов образует конечный
алфавит
исходных
символов.. Слова конечной длины в конечных
алфавитах - обычный тип алгоритмических
данных, число символов в слове– единица
измерения информации. Более сложный
алгоритмический объект – формула.
2)Данные
для своего размещ требуют памяти.
Память обычно считается однородной и
дискретной, т.е. состоит из одинак ячеек,
причем каждая ячейка может содержать
один символ алфавита данных. Т о, единицы
измерения объема данных и памяти
согласованы. 3)Алгоритм
состоит из отдельных элементарных
шагов,
причем множество различных шагов, из
которых составлен алгоритм, конечно.
Типичный пример множества элементарных
действий – система команд компьютера.
Обычно элементарный шаг имеет дело с
фиксированным числом символов.4)
Последовательность шагов алгоритма
детерминирована,
т.е. после каждого шага либо указывается,
какой шаг делать дальше, либо дается
команда остановки, после чего работа
алгоритма считается законченной.5)Требование
результативности
алгоритма, т.е. алгоритм должен
останавливаться после конечного числа
шагов (зависящего от данных) с указанием
того, что считать результатом. В частности,
при предъявлении алгоритма решения
задачи, например вычисления функции
f(x), нужно показать, что алгоритм
останавливается после конечного числа
шагов (сходится)
для любого x из области задания f. В
отличие от требований 1-4, сходимость
алгоритма обычно не удается установить
простым просмотром его описания. Вообще,
не существует общего способа проверки
сходимости алгоритма.
\\Следует
различать:a)Описание
алгоритма б)Механизм
реализации включающий средства пуска,
установки, реализации элементарных
шагов, выдачи результатов и обеспечения
детерминированности, т.е. управления
ходом вычисления.в)Процесс
реализации алгоритма, т.е. последовательность
шагов, которая будет порождена при
применении алгоритма к конкретным
данны///Алгоритм можно описать с помощью
блок-схемы,
т.е. графа, в котором вершинам соответствуют
шаги, а ребрам – переходы между шагами.
Язык блок-схем очень нагляден, однако,
он достаточно груб и отражает связи
лишь по управлению (что делать в следующий
момент времени, т.е. какому блоку передать
управление), а не по информации (где
этому блоку брать исходные данные).
\\Т.о,
при построении алгоритма в теории
алгоритмов используется следующий
подход: выбирается конечный набор
исходных объектов, которые объявляются
элементарными, и конечный набор построения
из них новых объектов. Данными при этом
считаются множества слов в конечных
алфавитах. Для уточнения детерминизма
используются либо блок схемы, либо
эквивалентные им словесные описания,
либо описание механизма реализации
алгоритма. Кроме того, нужно зафиксировать
набор элементарных шагов и договориться
об организации памяти.\\Рассматриваемые
алгоритмические модели формализуют
понятие «алгоритм». Это значит, что они
должны. допускать описание любых
алгоритмов. Основные цели создания
теории алгоритмов – универсальность
и связанная с ней возможность говорить
в рамках какой-либо модели о свойствах
алгоритмов вообще. Можно выделить три
основных типа универсальных алгоритмических
моделей, различающихся исходными
эвристическими соображениями относительно
того, что такое алгоритм. Первый тип
связывает понятие алгоритма с традиционным
понятием математики – вычислениями и
числовыми функциями. Наиболее развитая
модель этого типа – рекурсивные
функции
– является первой реализацией алгоритма.
Второй основан на представлении об
алгоритме как о некотор детерминированном
устройстве, способном выполнять в каждый
момент времени весьма примитивные
операции. Основной теоретической моделью
этого типа является машина
Тьюринга,
созданная в 30-х. Третий тип– это
преобразование слов в произвольных
алфавитах, в которых элементарными
операциями являются подстановки. Примеры
моделей этого типа – канонические
системы Поста и нормальные алгоритмы
Маркова. \\Машина
Тьюрин состоит
из: 1)управляющего
устройства, которое может находиться
в одном из состояний, образующих конечное
множество Q = {q1,…,
qn}2)ленты,
разбитой на ячейки, в каждой из которых
может быть записан один из символов
конечного алфавита A = {a1,
… am}3)устройства
обращения к ленте, т.е. считывающей и
пишущей головки, которая в каждый момент
времени обозревает ячейку ленты и в
зависимости от символа в этой ячейке и
состояния управляющего устройства,
записывает в нее символ, сдвигается на
ячейку влево или вправо или остается
на месте, при этом управляющее устройство
переходит в новое состояние (или остается
в старом). Среди состояний управляющего
устройства выделены начальное состояние
q1
и заключительное qz.
Память
МТ
–конечное множество состояний (внутренняя
память) и лента (внешняя память). Лента
бесконечна в обе стороны, однако в начал
момент времени только конечное число
ячеек заполнено непустыми символами,
остальные же содержат пустой символ
 (пробел).
Данные
МТ
–слова в алфавите ленты; на ленте
записываются и исходные данные и конечные
результаты. Элементарные
шаги МТ
–считывание и запись символов, сдвиг
головки на ячейку влево и вправо, а также
переход управляющего устройства в
следующее состояние. \\\Конкретная
машина Тьюринга задаётся перечислением
элементов множества букв алфавита A,
множества состояний Q и набором правил,
по которым работает машина. Они имеют
вид: qiaj→qi1aj1dk (1)
(если головка находится в состоянии qi,
а в обозреваемой ячейке записана буква
aj,
то головка переходит в состояние qi1,
в ячейку вместо aj записывается
aj1,
головка делает движение dk,
которое имеет три варианта: на ячейку
влево (L), на ячейку вправо (R), остаться
на месте (N)). Для каждой возможной
конфигурации <qi,
aj>
имеется ровно одно правило. Правил нет
только для заключительного состояния,
попав в которое машина останавливается.
Кроме того, необходимо указать конечное
и начальное состояния, начальную
конфигурацию на ленте и расположение
головки машины.
Задать МТ можно либо системой правил,
имеющих вид (1), либо таблицей, либо
блок-схемой (диаграммой переходов).Пример:
Машина с алфавитом
(пробел).
Данные
МТ
–слова в алфавите ленты; на ленте
записываются и исходные данные и конечные
результаты. Элементарные
шаги МТ
–считывание и запись символов, сдвиг
головки на ячейку влево и вправо, а также
переход управляющего устройства в
следующее состояние. \\\Конкретная
машина Тьюринга задаётся перечислением
элементов множества букв алфавита A,
множества состояний Q и набором правил,
по которым работает машина. Они имеют
вид: qiaj→qi1aj1dk (1)
(если головка находится в состоянии qi,
а в обозреваемой ячейке записана буква
aj,
то головка переходит в состояние qi1,
в ячейку вместо aj записывается
aj1,
головка делает движение dk,
которое имеет три варианта: на ячейку
влево (L), на ячейку вправо (R), остаться
на месте (N)). Для каждой возможной
конфигурации <qi,
aj>
имеется ровно одно правило. Правил нет
только для заключительного состояния,
попав в которое машина останавливается.
Кроме того, необходимо указать конечное
и начальное состояния, начальную
конфигурацию на ленте и расположение
головки машины.
Задать МТ можно либо системой правил,
имеющих вид (1), либо таблицей, либо
блок-схемой (диаграммой переходов).Пример:
Машина с алфавитом
 ,
состояниями {q1, q2} и системой команд
,
состояниями {q1, q2} и системой команд
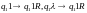 из любой начальной конфигурации будет
работать бесконечно, заполняя единицами
всю ленту вправо.
Если
из любой начальной конфигурации будет
работать бесконечно, заполняя единицами
всю ленту вправо.
Если
 ,
то говорят, что МТ преобразует
слово
,
то говорят, что МТ преобразует
слово
 в
в
 и обозначают
и обозначают
 .
Также запись
.
Также запись
 обозначает МТ с исходным значением
.
Полное состояние МТ
обозначает МТ с исходным значением
.
Полное состояние МТ
 называется
конфигурацией
или машинным
словом.
Например, конфигурация с внутренним
состоянием qi,
в котором на ленте записано abcde, а головка
обозревает d, запишется как abcqide.
Универсальная
машина Тьюринга
- машина
Тьюр, которая может заменить собой
любую машину Тьюр. Получив на вход
программу и входные данные, она вычисляет
ответ, который вычислила бы по входным
данным машина Тьюринга, чья программа
была дана на вход.Формальное
определение Программу
любой детерминированной машины Тьюринга
можно записать, используя некоторый
конечный алфавит, состоящий из символов
состояния, скобок, стрелки и т. п.;
обозначим этот машинный алфавит как Σ1.
Тогда универсальной машиной Тьюринга U для
класса машин с алфавитом Σ2 и k входными
лентами называется машина Тьюринга
с k+1 входной лентой и алфавитом
называется
конфигурацией
или машинным
словом.
Например, конфигурация с внутренним
состоянием qi,
в котором на ленте записано abcde, а головка
обозревает d, запишется как abcqide.
Универсальная
машина Тьюринга
- машина
Тьюр, которая может заменить собой
любую машину Тьюр. Получив на вход
программу и входные данные, она вычисляет
ответ, который вычислила бы по входным
данным машина Тьюринга, чья программа
была дана на вход.Формальное
определение Программу
любой детерминированной машины Тьюринга
можно записать, используя некоторый
конечный алфавит, состоящий из символов
состояния, скобок, стрелки и т. п.;
обозначим этот машинный алфавит как Σ1.
Тогда универсальной машиной Тьюринга U для
класса машин с алфавитом Σ2 и k входными
лентами называется машина Тьюринга
с k+1 входной лентой и алфавитом ![]() такая,
что если подать на первые k лент
входное значение, а на k+1 — правильно
записанный код некоторой машины
Тьюринга M1, то U выдаст тот же
ответ, какой выдала бы на этих входных
данных M1, или будет работать бесконечно
долго, если M1 на этих данных не
остановится.Теорема
об универсальной машине Тьюринга
утверждает, что такая машина существует
и моделирует другие машины с не более
чем квадратичным замедлением (то есть
если исходная машина произвела t шагов,
то универсальная произведёт не более ct²).
Тезис
Тьюринга: «Всякий
алгоритм может быть реализован машиной
Тьюринга». Доказать тезис Тьюринга
нельзя, поскольку само понятие алгоритма
является неточным. Тезис
Черча
является аналогом тезиса Тьюринга для
рекурсивных функций. Он гласит: «Всякая
функция, вычислимая некоторым алгоритмом,
частично рекурсивна»Из сопоставления
двух тезисов вытекает утверждение:
«функция вычислима МТ тогда и только
тогда, когда она частично-рекурсивна».
Проблема
остановки: требование
результативности можно сформулировать
следующим образом – по любому алгоритму
А и данным d определить, приведет ли
работа алгоритма А при исходных данных
d к результату или нет. Можно ли построить
алгоритм В, такой что В(А, d) = И, если А(d)
дает результат и В(А, d) = Л, иначе. В силу
тезиса Тьюринга эту задачу можно
сформулировать как задачу построения
соответствующей МТ. Теорема:
не существует МТ, решающей проблемы
остановки для произвольной МТ. В силу
тезиса Тьюринга невозможность построения
МТ означает отсутствие алгоритма решения
данной проблемы. Поэтому данная теорема
дает первый пример алгоритмически
неразрешимой проблемы.
Определение:
Функция
называется вычислимой,
если существует вычисляющий ее алгор.
Проблема эквивалентн алгоритмов является
неразрешимой: по двум заданным алгоритмам
нельзя узнать, вычисляют они одну и ту
же функцию, или нет. Рекурсивные
функцииТермин рекурсивные
функции в теории
вычислимости используют для
обозначения трёх множеств функций
1)примит
рекурсив
2)общерекурсивные
;3)частично
рекурсивные функции.Последние
совпадают с множеством вычислимых
по Тьюрингу функций. Множество частично
рекурсивных функции включает в себя
множество общерекурсивных функции, а
общерекурсивные функции включают в
себя примитивно рекурсивные
функции..Примитивно
рекурсивные функцииОпределение
понятия примитивно рекурсивной функции
является индуктивным. Оно состоит из
указания класса базовых примитивно
рекурсивных функций и двух операторов
(подстановки и примитивной
рекурсии),
позволяющих строить новые примитивно
рекурсивные функции на основе уже
имеющихся.К числу базовых примитивно
рекурсивных функций относятся функции
следующих трёх видов:1)Нулевая
функция O —
функция без аргументов, всегда
возвращающая 0.
2)Функция
следования S одного
переменного, сопоставляющая любому
натуральному числу x непосредственно
следующее за ним натуральное число x +
1.
3)Функции
такая,
что если подать на первые k лент
входное значение, а на k+1 — правильно
записанный код некоторой машины
Тьюринга M1, то U выдаст тот же
ответ, какой выдала бы на этих входных
данных M1, или будет работать бесконечно
долго, если M1 на этих данных не
остановится.Теорема
об универсальной машине Тьюринга
утверждает, что такая машина существует
и моделирует другие машины с не более
чем квадратичным замедлением (то есть
если исходная машина произвела t шагов,
то универсальная произведёт не более ct²).
Тезис
Тьюринга: «Всякий
алгоритм может быть реализован машиной
Тьюринга». Доказать тезис Тьюринга
нельзя, поскольку само понятие алгоритма
является неточным. Тезис
Черча
является аналогом тезиса Тьюринга для
рекурсивных функций. Он гласит: «Всякая
функция, вычислимая некоторым алгоритмом,
частично рекурсивна»Из сопоставления
двух тезисов вытекает утверждение:
«функция вычислима МТ тогда и только
тогда, когда она частично-рекурсивна».
Проблема
остановки: требование
результативности можно сформулировать
следующим образом – по любому алгоритму
А и данным d определить, приведет ли
работа алгоритма А при исходных данных
d к результату или нет. Можно ли построить
алгоритм В, такой что В(А, d) = И, если А(d)
дает результат и В(А, d) = Л, иначе. В силу
тезиса Тьюринга эту задачу можно
сформулировать как задачу построения
соответствующей МТ. Теорема:
не существует МТ, решающей проблемы
остановки для произвольной МТ. В силу
тезиса Тьюринга невозможность построения
МТ означает отсутствие алгоритма решения
данной проблемы. Поэтому данная теорема
дает первый пример алгоритмически
неразрешимой проблемы.
Определение:
Функция
называется вычислимой,
если существует вычисляющий ее алгор.
Проблема эквивалентн алгоритмов является
неразрешимой: по двум заданным алгоритмам
нельзя узнать, вычисляют они одну и ту
же функцию, или нет. Рекурсивные
функцииТермин рекурсивные
функции в теории
вычислимости используют для
обозначения трёх множеств функций
1)примит
рекурсив
2)общерекурсивные
;3)частично
рекурсивные функции.Последние
совпадают с множеством вычислимых
по Тьюрингу функций. Множество частично
рекурсивных функции включает в себя
множество общерекурсивных функции, а
общерекурсивные функции включают в
себя примитивно рекурсивные
функции..Примитивно
рекурсивные функцииОпределение
понятия примитивно рекурсивной функции
является индуктивным. Оно состоит из
указания класса базовых примитивно
рекурсивных функций и двух операторов
(подстановки и примитивной
рекурсии),
позволяющих строить новые примитивно
рекурсивные функции на основе уже
имеющихся.К числу базовых примитивно
рекурсивных функций относятся функции
следующих трёх видов:1)Нулевая
функция O —
функция без аргументов, всегда
возвращающая 0.
2)Функция
следования S одного
переменного, сопоставляющая любому
натуральному числу x непосредственно
следующее за ним натуральное число x +
1.
3)Функции ![]() ,
где
,
где ![]() ,
от n переменных, сопоставляющие любому
упорядоченному набору
,
от n переменных, сопоставляющие любому
упорядоченному набору ![]() натуральных
чисел число xm из
этого набора. \\\\\Операторы
подстановки и примитивной рекурсии
определяются следующим образом:Оператор
подстановки.
Пусть f —
функция от m переменных, а
натуральных
чисел число xm из
этого набора. \\\\\Операторы
подстановки и примитивной рекурсии
определяются следующим образом:Оператор
подстановки.
Пусть f —
функция от m переменных, а ![]() —
упорядоченный набор функций от n переменных
каждая. Тогда результатом подстановки
функций gk в
функцию f называется
функция h от n переменных,
сопоставляющая любому упорядоченному
набору
натуральных
чисел число
—
упорядоченный набор функций от n переменных
каждая. Тогда результатом подстановки
функций gk в
функцию f называется
функция h от n переменных,
сопоставляющая любому упорядоченному
набору
натуральных
чисел число![]() .Оператор
примитивной рекурсии.
Пусть f —
функция от n переменных, а g —
функция от n +
2 переменных.
Тогда результатом применения оператора
примитивной рекурсии к паре
функций f и g называется
функция h от n +
1 переменной
вида
.Оператор
примитивной рекурсии.
Пусть f —
функция от n переменных, а g —
функция от n +
2 переменных.
Тогда результатом применения оператора
примитивной рекурсии к паре
функций f и g называется
функция h от n +
1 переменной
вида![]()
![]() Множес примитивно
рекурсивных функций —миним
множество, содержащее все базовые
функции и замкнутое относительно
указанных операторов подстановки и
примитивной рекурсии.
Примеры
функ Сложения двух
натуральных чисел (
Множес примитивно
рекурсивных функций —миним
множество, содержащее все базовые
функции и замкнутое относительно
указанных операторов подстановки и
примитивной рекурсии.
Примеры
функ Сложения двух
натуральных чисел (![]() )
мобыть рассмотрена в качестве примитивно
рекурсивной функции двух переменных,
получаемой в результате применения
оператора примитивной рекурсии к
функциям
)
мобыть рассмотрена в качестве примитивно
рекурсивной функции двух переменных,
получаемой в результате применения
оператора примитивной рекурсии к
функциям ![]() и
и ![]() ,
вторая из которых получается подстановкой
основной функции
,
вторая из которых получается подстановкой
основной функции ![]() в
основную функцию S:
в
основную функцию S:
![]()
![]()
![]() Частично
рекурсивные функции определяются
аналогичным образом, только к двум
операторам подстановки и примитивной
рекурсии добавляется ещё.Оператор
минимизации аргумента.:
Пусть f —
функция от n натуральных переменных.
Тогда результатом применения оператора
минимума аргумента к функции fназывается
функция h от n −
1 переменной,
задаваемая следующим определением:
Частично
рекурсивные функции определяются
аналогичным образом, только к двум
операторам подстановки и примитивной
рекурсии добавляется ещё.Оператор
минимизации аргумента.:
Пусть f —
функция от n натуральных переменных.
Тогда результатом применения оператора
минимума аргумента к функции fназывается
функция h от n −
1 переменной,
задаваемая следующим определением:![]() ,
при условии
,
при условии ![]() То
есть функция h возвращает
миним значен последнего аргумента
функции f,
при котором её значение равно 0.Важным
моментом является что частично рекурсивные
функции для некоторых значений аргумента
могут быть не определены, так как оператор
минимизации аргумента не всегда корректно
определён, именно, функция f может быть
не равной нулю ни при каких значениях
аргументов.Собственно, оттого, что
частично рекурсивные функции могут
иметь корректно определённое значение
лишь на части аргументов, и пошло их
название. Общерекурсивные
функции —
это подмножество частично рекурсивных
функций, определённых для всех значений
аргументов. Задача определения того,
является ли частично рекурсивная функция
с данным описанием общерекурсивной или
нет, алгоритмически
неразрешима.
Свойства
любая
примитивно рекурсивная функция является
частично рекурсивной, примитивно
рекурсивная функция определена везде
и поэтому является общерекурсивной.Сложно
привести пример общерекурсивной функции,
не являющейся примитивно рекурсивной.8.
Общие
понятия о формальных системах и методах
формализации. Формальные системы
– это системы операций над объектами,
понимаемыми как последовательности
символов; сами операции также являются
операциями над символами. Объекты и
операции над ними рассматриваются чисто
формально, без каких бы то ни было
содержательных интерпретаций символов.
Предполагается, что между символами не
существует никаких связей и отношений,
кроме тех, которые явно описаны средствами
самой формальной системы. \\\Формализацией
задачи называется ее уточнение и явное
описание таким образом, чтобы избежать
любой неоднозначности в ее извлечении.
Нужно четко описать все, что существенно
для решения задачи. \\\\Принципы
построения формальной системы
Всякая формальная система определяется:
1) языком, т.е. некоторым множеством
высказываний, имеющих смысл с точки
зрения этой теории 2) совокупностью
теорем – подмножеством языка, состоящим
из высказываний, истинных в данной
теории..\\\\\Форма́льная
систе́ма (или форма́льная
тео́рия) — результат строгой формализации теории,
предполагающей полную абстракцию от
смысла слов используемого языка, причем
все условия, регулирующие употребление
этих слов в теории, явно высказаны
посредством аксиом и
правил, позволяющих вывести одну фразу
из других[1].
\\\Формальная
система
– это совокупность абстрактных объектов,
не связанных с внешним миром, в котором
представлены правила оперирования
множеством символов в строго синтаксической
трактовке без учета смыслового содержания.
\\\\Теория
формальных систем ставит целью ответить
на вопросы: «как должна быть построена
теория, чтобы в ней не возникло
противоречий?». Фундаментальной идеей
в ней является идея
формализации теории,
т.е. последовательного проведения
аксиоматического метода построения
теории. Формальная
система (или исчисление) строится
следующим образом.
1)Определяется
конечный алфавит
теории. Из символов алфавита строится
множество формул,
или правильно построенных выражений,
образующих язык теории. Это множество
задается конструктивными средствами
следовательно, перечислимо. Обычно оно
и разрешимо. (Справка:
множество М называется разрешимым
(или рекурсивным), если существует
алгоритм АМ,
который по любому объекту a дает ответ,
принадлежит a множеству М или нет.
Множество М называется перечислимым,
если существует общерекурсивная функция
То
есть функция h возвращает
миним значен последнего аргумента
функции f,
при котором её значение равно 0.Важным
моментом является что частично рекурсивные
функции для некоторых значений аргумента
могут быть не определены, так как оператор
минимизации аргумента не всегда корректно
определён, именно, функция f может быть
не равной нулю ни при каких значениях
аргументов.Собственно, оттого, что
частично рекурсивные функции могут
иметь корректно определённое значение
лишь на части аргументов, и пошло их
название. Общерекурсивные
функции —
это подмножество частично рекурсивных
функций, определённых для всех значений
аргументов. Задача определения того,
является ли частично рекурсивная функция
с данным описанием общерекурсивной или
нет, алгоритмически
неразрешима.
Свойства
любая
примитивно рекурсивная функция является
частично рекурсивной, примитивно
рекурсивная функция определена везде
и поэтому является общерекурсивной.Сложно
привести пример общерекурсивной функции,
не являющейся примитивно рекурсивной.8.
Общие
понятия о формальных системах и методах
формализации. Формальные системы
– это системы операций над объектами,
понимаемыми как последовательности
символов; сами операции также являются
операциями над символами. Объекты и
операции над ними рассматриваются чисто
формально, без каких бы то ни было
содержательных интерпретаций символов.
Предполагается, что между символами не
существует никаких связей и отношений,
кроме тех, которые явно описаны средствами
самой формальной системы. \\\Формализацией
задачи называется ее уточнение и явное
описание таким образом, чтобы избежать
любой неоднозначности в ее извлечении.
Нужно четко описать все, что существенно
для решения задачи. \\\\Принципы
построения формальной системы
Всякая формальная система определяется:
1) языком, т.е. некоторым множеством
высказываний, имеющих смысл с точки
зрения этой теории 2) совокупностью
теорем – подмножеством языка, состоящим
из высказываний, истинных в данной
теории..\\\\\Форма́льная
систе́ма (или форма́льная
тео́рия) — результат строгой формализации теории,
предполагающей полную абстракцию от
смысла слов используемого языка, причем
все условия, регулирующие употребление
этих слов в теории, явно высказаны
посредством аксиом и
правил, позволяющих вывести одну фразу
из других[1].
\\\Формальная
система
– это совокупность абстрактных объектов,
не связанных с внешним миром, в котором
представлены правила оперирования
множеством символов в строго синтаксической
трактовке без учета смыслового содержания.
\\\\Теория
формальных систем ставит целью ответить
на вопросы: «как должна быть построена
теория, чтобы в ней не возникло
противоречий?». Фундаментальной идеей
в ней является идея
формализации теории,
т.е. последовательного проведения
аксиоматического метода построения
теории. Формальная
система (или исчисление) строится
следующим образом.
1)Определяется
конечный алфавит
теории. Из символов алфавита строится
множество формул,
или правильно построенных выражений,
образующих язык теории. Это множество
задается конструктивными средствами
следовательно, перечислимо. Обычно оно
и разрешимо. (Справка:
множество М называется разрешимым
(или рекурсивным), если существует
алгоритм АМ,
который по любому объекту a дает ответ,
принадлежит a множеству М или нет.
Множество М называется перечислимым,
если существует общерекурсивная функция
 ,
такая что
,
такая что
 ,
если и только если для некоторого x
,
если и только если для некоторого x
 (множество М является областью значений
общерекурсивной функции).)2)Выделяется
подмножество формул, называемых аксиомами
теории.
Множество может быть и бесконечным; во
всяком случае оно должно быть
разрешимо.3)Задаются
правила вывода теории. Правило вывода
(множество М является областью значений
общерекурсивной функции).)2)Выделяется
подмножество формул, называемых аксиомами
теории.
Множество может быть и бесконечным; во
всяком случае оно должно быть
разрешимо.3)Задаются
правила вывода теории. Правило вывода
![]() - это вычислимое отношение на множестве
формул. Если формулы
- это вычислимое отношение на множестве
формул. Если формулы
 находятся в отношении R, то формула G
называется непосредственно
выводимой
из
находятся в отношении R, то формула G
называется непосредственно
выводимой
из
 по правилу R:
по правилу R:
 .
Формулы
называются посылками правила R, а G –
его следствием или заключением.
\\\\\Выводом
формулы В из формул
.
Формулы
называются посылками правила R, а G –
его следствием или заключением.
\\\\\Выводом
формулы В из формул
 называется последовательность формул
называется последовательность формул
 ,
такая что Fm=B,
а любая Fi
(i=1…m)
есть либо аксиома, либо одна из исходных
формул
,
либо непосредственно выводима из
,
такая что Fm=B,
а любая Fi
(i=1…m)
есть либо аксиома, либо одна из исходных
формул
,
либо непосредственно выводима из
![]() (или
какого-то из их подмножества) по одному
из правил вывода. Если существует вывод
В из
,
то говорят, что В выводима из
и обозначают:
(или
какого-то из их подмножества) по одному
из правил вывода. Если существует вывод
В из
,
то говорят, что В выводима из
и обозначают:
 .
Формулы
называют посылками
или
гипотезами
вывода.
Доказательством
формулы В в теории Т называется вывод
В из пустого множества формул, т.е. вывод,
в котором в качестве исходных формул
используются только аксиомы. Формула
В, для которой существует доказательство,
называется доказуемой
формулой или теоремой
теории Т; обозначается -
.
Формулы
называют посылками
или
гипотезами
вывода.
Доказательством
формулы В в теории Т называется вывод
В из пустого множества формул, т.е. вывод,
в котором в качестве исходных формул
используются только аксиомы. Формула
В, для которой существует доказательство,
называется доказуемой
формулой или теоремой
теории Т; обозначается -
 .\\\Теория
Т называется формально
непротиворечивой,
если не существует формулы F, такой что
.\\\Теория
Т называется формально
непротиворечивой,
если не существует формулы F, такой что
 являются теоремами теории Т, т.е. в Т
невыводимы одновременно формула и ее
отрицание. \\\\\Если множество форму
семантически
непротиворечиво (т.е.
ни одна из теорем не является противоречивой,
т.е. ложной в любой интерпретации - когда
ее отрицание общезначимо, т.е. истинно
в любой интерпретации), то оно и формально
непротиворечиво\\\\ Пусть имеется
содержательная теория S, с другой стороны
– формальная теория Т. В каких случаях
можно утверждать, что Т является
удовлетворительной формализацией S?
Необходимым признаком является условие,
чтобы S была моделью Т, т.е. чтобы
существовало отображение, при котором
всякая теорема теории Т отображается
в истинное высказывание из S. Однако,
одного этого условия недостаточно,
иначе для формализации любой теории S
хватило бы исчисления предикатов - для
него любое множество является моделью.
Исчерпывающей формализацией S будет
такая теория Т, для которой выполняется
и обратное соответствие: каждое истинное
высказывание теории S отображается в
некоторую теорему теории Т. Теория Т с
таким свойством называется полной
относительно S. \\\\Исчисление высказываний
полно относительно алгебры высказываний,
что следует из следующих теорем:Теорема:
Всякая теорема исчисления высказываний
является тождественно-истинным
высказыванием. Теорема:
Всякая тождественно-истинная формула
является теоремой исчисления
высказываний.Теорема:
Всякая доказуемая формула исчисления
предикатов тождественно-истинна.
Теорема:
Всякая общезначимая предикатная формула
доказуема в исчислении
предикатов.\\\\\\Формальная теория Т
называется разрешимой,
если существует алгоритм, который для
любой формулы языка определяет, является
она теоремой в Т или нет. Теорема:
Исчисление высказываний
разрешимо.\\\\\\Разрешающий алгоритм для
формулы F заключается в вычислении
значений F на всех наборах значений ее
переменных. Ввиду полноты исчисления
высказываний F является его теоремой,
если и только если она истинна на всех
наборах. \\\\Теорема
(Черч):
Исчисление предикатов неразрешимо.
являются теоремами теории Т, т.е. в Т
невыводимы одновременно формула и ее
отрицание. \\\\\Если множество форму
семантически
непротиворечиво (т.е.
ни одна из теорем не является противоречивой,
т.е. ложной в любой интерпретации - когда
ее отрицание общезначимо, т.е. истинно
в любой интерпретации), то оно и формально
непротиворечиво\\\\ Пусть имеется
содержательная теория S, с другой стороны
– формальная теория Т. В каких случаях
можно утверждать, что Т является
удовлетворительной формализацией S?
Необходимым признаком является условие,
чтобы S была моделью Т, т.е. чтобы
существовало отображение, при котором
всякая теорема теории Т отображается
в истинное высказывание из S. Однако,
одного этого условия недостаточно,
иначе для формализации любой теории S
хватило бы исчисления предикатов - для
него любое множество является моделью.
Исчерпывающей формализацией S будет
такая теория Т, для которой выполняется
и обратное соответствие: каждое истинное
высказывание теории S отображается в
некоторую теорему теории Т. Теория Т с
таким свойством называется полной
относительно S. \\\\Исчисление высказываний
полно относительно алгебры высказываний,
что следует из следующих теорем:Теорема:
Всякая теорема исчисления высказываний
является тождественно-истинным
высказыванием. Теорема:
Всякая тождественно-истинная формула
является теоремой исчисления
высказываний.Теорема:
Всякая доказуемая формула исчисления
предикатов тождественно-истинна.
Теорема:
Всякая общезначимая предикатная формула
доказуема в исчислении
предикатов.\\\\\\Формальная теория Т
называется разрешимой,
если существует алгоритм, который для
любой формулы языка определяет, является
она теоремой в Т или нет. Теорема:
Исчисление высказываний
разрешимо.\\\\\\Разрешающий алгоритм для
формулы F заключается в вычислении
значений F на всех наборах значений ее
переменных. Ввиду полноты исчисления
высказываний F является его теоремой,
если и только если она истинна на всех
наборах. \\\\Теорема
(Черч):
Исчисление предикатов неразрешимо.
Несмотря
на полноту исчисления предикатов,
разрешающий алгоритм, связанный с
вычислением значений истинности
предикатных формул, построить не удается
в связи с бесконечностью предметной
области, которая приводит в общем случае
к бесконечным таблицам истинности.
Однако исчисление одноместных предикатов
разрешимо. То
же самой из Википедии:ПротиворечивостьТеория,
в которой множество теорем покрывает
всё множество формул (все формулы
являются теоремами, «истинными
высказываниями»), называется противоречивой.
В противном случае теория
называется непротиворечивойПолнотаТеория
называется полной, если в ней для
любой формулы F выводима либо
сама F, либо ее отрицание ![]() .
В противном случае, теория
содержит недоказуемые
утверждения (утверждения, которые
нельзя ни доказать, ни опровергнуть
средствами самой теории), и
называется неполной.Независимость
аксиомОтдельная
аксиома теории считается независимой,
если эту аксиому нельзя вывести из
остальных аксиом.. Вся система аксиом
теории называется независимой, если
каждая аксиома в ней независима.РазрешимостьТеория
называется разрешимой, если
существует эффективный
процесс (алгоритм), позволяющий
для любой формулы за конечное число
шагов определить, является она теоремой
или нет.Важнейшие
выводы 1)В
30-е гг. XX века Курт Гёдель показал,
что есть целый класс теорий первого
порядка, являющихся неполными. Более
того, формула, утверждающая непротиворечивость
теории, также невыводима средствами
самой теории (см. Теоремы
Гёделя о неполноте).
Этот вывод имел огромное значение для
математики, так как формальная арифметика
(а на ней базируется теория действительных
чисел, без которой нельзя представить
современную математику) является как
раз такой теорией первого порядка, а
следовательно, формальная арифметика
и все теории, содержащие ее, в том числе
теория действительных чисел, являются
неполными.2)Проблема
неразрешимости логики предикатов.
Чёрчем доказано, что не существует
алгоритма, который для любой формулы логики
предикатов устанавливает,
логически общезначима формула или
нет.3)Исчисление
высказываний является непротиворечивой,
полной, разрешимой теорией, причем все
три утверждения доказуемы в рамках
самой логики высказыванийпра́вило
резолю́ций Если
для двух дизъюнктов существует атомная
формула, которая в один дизъюнкт входит
положительно, а в другой отрицательно,
то, вычеркнув соответственно из одного
дизъюнкта положительное вхождение
атомной формулы, а из другого —
отрицательное, и объединив эти дизъюнкты,
мы получим дизъюнкт, называемый резольвентой.
Исходные дизъюнкты в таком случае
называются родительскими или
резольвируемыми, а вычеркнутые формулы
— контрарными
литералами.
Другими словами, резольвента — это
дизъюнкт, полученный из объединения
родительских дизъюнктов вычеркиванием
контрарных литералов.Графически это
можно изобразить так:(A
.
В противном случае, теория
содержит недоказуемые
утверждения (утверждения, которые
нельзя ни доказать, ни опровергнуть
средствами самой теории), и
называется неполной.Независимость
аксиомОтдельная
аксиома теории считается независимой,
если эту аксиому нельзя вывести из
остальных аксиом.. Вся система аксиом
теории называется независимой, если
каждая аксиома в ней независима.РазрешимостьТеория
называется разрешимой, если
существует эффективный
процесс (алгоритм), позволяющий
для любой формулы за конечное число
шагов определить, является она теоремой
или нет.Важнейшие
выводы 1)В
30-е гг. XX века Курт Гёдель показал,
что есть целый класс теорий первого
порядка, являющихся неполными. Более
того, формула, утверждающая непротиворечивость
теории, также невыводима средствами
самой теории (см. Теоремы
Гёделя о неполноте).
Этот вывод имел огромное значение для
математики, так как формальная арифметика
(а на ней базируется теория действительных
чисел, без которой нельзя представить
современную математику) является как
раз такой теорией первого порядка, а
следовательно, формальная арифметика
и все теории, содержащие ее, в том числе
теория действительных чисел, являются
неполными.2)Проблема
неразрешимости логики предикатов.
Чёрчем доказано, что не существует
алгоритма, который для любой формулы логики
предикатов устанавливает,
логически общезначима формула или
нет.3)Исчисление
высказываний является непротиворечивой,
полной, разрешимой теорией, причем все
три утверждения доказуемы в рамках
самой логики высказыванийпра́вило
резолю́ций Если
для двух дизъюнктов существует атомная
формула, которая в один дизъюнкт входит
положительно, а в другой отрицательно,
то, вычеркнув соответственно из одного
дизъюнкта положительное вхождение
атомной формулы, а из другого —
отрицательное, и объединив эти дизъюнкты,
мы получим дизъюнкт, называемый резольвентой.
Исходные дизъюнкты в таком случае
называются родительскими или
резольвируемыми, а вычеркнутые формулы
— контрарными
литералами.
Другими словами, резольвента — это
дизъюнкт, полученный из объединения
родительских дизъюнктов вычеркиванием
контрарных литералов.Графически это
можно изобразить так:(A
![]() P, B
¬P) / A
B. Здесь A
B и B
¬P —
родительские дизъюнкты, P и ¬P —
контрарные литералы, A
B —
резольвента.Если родительские дизъюнкты
состояли только из контрарных литералов,
то резольвентой будет пустой
дизъюнкт.Пример. Правило
вывода "modus ponens" получается из
правила резолюции, если взять в качестве
родительских дизъюнктов C1=A, C2=¬A
B(
P, B
¬P) / A
B. Здесь A
B и B
¬P —
родительские дизъюнкты, P и ¬P —
контрарные литералы, A
B —
резольвента.Если родительские дизъюнкты
состояли только из контрарных литералов,
то резольвентой будет пустой
дизъюнкт.Пример. Правило
вывода "modus ponens" получается из
правила резолюции, если взять в качестве
родительских дизъюнктов C1=A, C2=¬A
B( ![]() A
A ![]() B).
Контрарными литералами в применении
этого правила будут A и ¬A,
резольвентой — формула B.\\\\\Сформулируем
правило резолюции для логики первого
порядка.\\\\Пусть имеется два
дизъюнкта C1 и C2,
у которых нет общих переменных, L1 —
литерал, входящий в дизъюнкт C1, L2 —
литерал, входящий в дизъюнктC2.
Если литералы имеют наибольший общий
унификатор θ,
то
дизъюнкт (C1θ–L1θ)
B).
Контрарными литералами в применении
этого правила будут A и ¬A,
резольвентой — формула B.\\\\\Сформулируем
правило резолюции для логики первого
порядка.\\\\Пусть имеется два
дизъюнкта C1 и C2,
у которых нет общих переменных, L1 —
литерал, входящий в дизъюнкт C1, L2 —
литерал, входящий в дизъюнктC2.
Если литералы имеют наибольший общий
унификатор θ,
то
дизъюнкт (C1θ–L1θ)![]() (C2θ–L2θ) называется резольвентой дизъюнктов C1 и C2.
Литералы L1 и L2 называются
контрарными литералами. То же правило
записывается в графическом виде как(A
P1,
B
¬P2)/(A
B)θ Здесь P1 и P2 —
контрарные литералы, (A
B)θ —
резольвента, полученная из
дизъюнкта (A
B) применением
унификатора θ, A
P1 и B
P2 —
родительские дизъюнкты, а θ —
наибольший общий унификатор P1 и P2.Метод
резолюций является
обобщением метода "доказательства
от противного".
Вместо того чтобы пытаться вывести
некоторую формулу-гипотезу из имеющегося
непротиворечивого множества аксиом,
мы добавляем отрицание нашей формулы
к множеству аксиом и пытаемся вывести
из него противоречие. Если нам удается
это сделать, мы приходим к выводу, что
исходная формула была выводима из
множества аксиом. \\\\\Добавим отрицание
исходной формулы к множеству посылок,
преобразуем каждую из этих формул во
множество дизъюнктов, объединим
получившиеся множества дизъюнктов и
попытаемся вывести из этого множества
дизъюнктов противоречие (пустой
дизъюнкт ℵ).
Для этого будем выбирать из нашего
множества дизъюнкты, содержащие
унифицируемые контрарные литералы,
вычислять их резольвенту по правилу
резолюции, добавлять ее к исследуемому
множеству дизъюнктов. Этот процесс
будем продолжать до тех пор, пока не
выведем пустой дизъюнкт.\\\\\\Возможны,
вообще говоря, три случая:1)Этот
процесс никогда не завершается.2)Среди
текущего множества дизъюнктов не
окажется таких, к которым можно применить
правило резолюции. Это означает, что
множество дизъюнктов выполнимо, и,
значит, исходная формула не выводима.3)На
очередном шаге получена пустая
резольвента. Это означает, что множество
дизъюнктов невыполнимо и, следовательно,
начальная формула выводима.
(C2θ–L2θ) называется резольвентой дизъюнктов C1 и C2.
Литералы L1 и L2 называются
контрарными литералами. То же правило
записывается в графическом виде как(A
P1,
B
¬P2)/(A
B)θ Здесь P1 и P2 —
контрарные литералы, (A
B)θ —
резольвента, полученная из
дизъюнкта (A
B) применением
унификатора θ, A
P1 и B
P2 —
родительские дизъюнкты, а θ —
наибольший общий унификатор P1 и P2.Метод
резолюций является
обобщением метода "доказательства
от противного".
Вместо того чтобы пытаться вывести
некоторую формулу-гипотезу из имеющегося
непротиворечивого множества аксиом,
мы добавляем отрицание нашей формулы
к множеству аксиом и пытаемся вывести
из него противоречие. Если нам удается
это сделать, мы приходим к выводу, что
исходная формула была выводима из
множества аксиом. \\\\\Добавим отрицание
исходной формулы к множеству посылок,
преобразуем каждую из этих формул во
множество дизъюнктов, объединим
получившиеся множества дизъюнктов и
попытаемся вывести из этого множества
дизъюнктов противоречие (пустой
дизъюнкт ℵ).
Для этого будем выбирать из нашего
множества дизъюнкты, содержащие
унифицируемые контрарные литералы,
вычислять их резольвенту по правилу
резолюции, добавлять ее к исследуемому
множеству дизъюнктов. Этот процесс
будем продолжать до тех пор, пока не
выведем пустой дизъюнкт.\\\\\\Возможны,
вообще говоря, три случая:1)Этот
процесс никогда не завершается.2)Среди
текущего множества дизъюнктов не
окажется таких, к которым можно применить
правило резолюции. Это означает, что
множество дизъюнктов выполнимо, и,
значит, исходная формула не выводима.3)На
очередном шаге получена пустая
резольвента. Это означает, что множество
дизъюнктов невыполнимо и, следовательно,
начальная формула выводима.
В
сущности, метод
резолюций несовершенен
и приводит к "комбинаторному взрыву".
Однако некоторые его разновидности
(или стратегии) довольно эффективны.
Одной из самых удачных стратегий
является линейная или SLD-резолюция для хорновских
дизъюнктов (Linear
resolution with Selection function for Definition clauses), то есть
дизъюнктов, содержащих не более одного
положительного литерала. Их
называют предложениями или клозами.\\\\\Если
дизъюнкт состоит только из одного
положительного литерала, он
называется фактом.
Дизъюнкт, состоящий только из отрицательных
литералов, называется вопросом (или целью или запросом).
Если дизъюнкт содержит и позитивный, и
негативные литералы, он называется
правилом. Правило вывода выглядит
примерно следующим образом ¬A1
¬A2...¬An
B.
Это эквивалентно формуле A1 ![]() A2...
An
B
Логической
программой называется
конечное непустое множество
фактов и правил.При выполнении программы
к множеству фактов и правил добавляется
отрицание вопроса, после чего
используется линейная
резолюция.
Ее специфика в том, что правило резолюции
применяется не к произвольным дизъюнктам
из программы. Берется самый левый литерал
цели (подцель) и первый унифицируемый
с ним дизъюнкт. К ним применяется правило
резолюции. Полученная резольвента
добавляется в программу в качестве
нового вопроса. И так до тех пор, пока
не будет получен пустой дизъюнкт, что
будет означать успех, или до тех пор,
пока очередную подцель будет невозможно
унифицировать ни с одним дизъюнктом
программы, что будет означать неудачу.\\\\В
последнем случае включается так
называемый бэктрекинг — механизм
возврата, который осуществляет откат
программы к той точке, в которой выбирался
унифицирующийся с последней подцелью
дизъюнкт. Для этого точка, где выбирался
один из возможных унифицируемых с
подцелью дизъюнктов, запоминается в
специальном стеке, для последующего
возврата к ней и выбора альтернативы в
случае неудачи. При откате все переменные,
которые были означены в
результате унификации после
этой точки, опять становятся
свободными.\\\\\В итоге выполнение
программы может завершиться неудачей,
если одну из подцелей не удалось
унифицировать ни с одним дизъюнктом
программы, и может завершиться успешно,
если был выведен пустой дизъюнкт, а
может и просто зациклиться.\\\\\\\В математической
логике и автоматическом
доказательстве теорем, пра́вило
резолю́ций –
это правило вывода, восходящее к методу
доказательства теорем через поиск
противоречий; используется в логике
высказываний и логике
предикатов первого
порядка. Правило резолюций, применяемое
последовательно для спискарезольвент,
позволяет ответить на вопрос, существует
ли в исходном множестве логических
выражений противоречие. Исчисление
высказыванийПусть C1 и C2 -
два предложения в исчислении высказываний,
и пусть
A2...
An
B
Логической
программой называется
конечное непустое множество
фактов и правил.При выполнении программы
к множеству фактов и правил добавляется
отрицание вопроса, после чего
используется линейная
резолюция.
Ее специфика в том, что правило резолюции
применяется не к произвольным дизъюнктам
из программы. Берется самый левый литерал
цели (подцель) и первый унифицируемый
с ним дизъюнкт. К ним применяется правило
резолюции. Полученная резольвента
добавляется в программу в качестве
нового вопроса. И так до тех пор, пока
не будет получен пустой дизъюнкт, что
будет означать успех, или до тех пор,
пока очередную подцель будет невозможно
унифицировать ни с одним дизъюнктом
программы, что будет означать неудачу.\\\\В
последнем случае включается так
называемый бэктрекинг — механизм
возврата, который осуществляет откат
программы к той точке, в которой выбирался
унифицирующийся с последней подцелью
дизъюнкт. Для этого точка, где выбирался
один из возможных унифицируемых с
подцелью дизъюнктов, запоминается в
специальном стеке, для последующего
возврата к ней и выбора альтернативы в
случае неудачи. При откате все переменные,
которые были означены в
результате унификации после
этой точки, опять становятся
свободными.\\\\\В итоге выполнение
программы может завершиться неудачей,
если одну из подцелей не удалось
унифицировать ни с одним дизъюнктом
программы, и может завершиться успешно,
если был выведен пустой дизъюнкт, а
может и просто зациклиться.\\\\\\\В математической
логике и автоматическом
доказательстве теорем, пра́вило
резолю́ций –
это правило вывода, восходящее к методу
доказательства теорем через поиск
противоречий; используется в логике
высказываний и логике
предикатов первого
порядка. Правило резолюций, применяемое
последовательно для спискарезольвент,
позволяет ответить на вопрос, существует
ли в исходном множестве логических
выражений противоречие. Исчисление
высказыванийПусть C1 и C2 -
два предложения в исчислении высказываний,
и пусть ![]() ,
а
,
а ![]() ,
где P -
пропозициональная переменная,
а C'1 и C'2 -
любые предложения (в частности, может
быть, пустые или состоящие только из
одного литерала).Правило
вывода
,
где P -
пропозициональная переменная,
а C'1 и C'2 -
любые предложения (в частности, может
быть, пустые или состоящие только из
одного литерала).Правило
вывода![]() называется правилом
резолюции. Предложения C1 и C2 называются резольвируемыми (или родительскими),предложение
называется правилом
резолюции. Предложения C1 и C2 называются резольвируемыми (или родительскими),предложение ![]() - резольвентой,
а формулы P и
- резольвентой,
а формулы P и ![]() - контрарными литералами.
Исчисление
предикатовПусть C1 и C2 -
два предложения в исчислении предикатов.
Правило вывода
- контрарными литералами.
Исчисление
предикатовПусть C1 и C2 -
два предложения в исчислении предикатов.
Правило вывода![]() называется
правилом резолюции в исчислении
предикатов, если в предложениях C1 и C2 существуют
унифицированные контрарные литералы P1 и P2,
то есть
называется
правилом резолюции в исчислении
предикатов, если в предложениях C1 и C2 существуют
унифицированные контрарные литералы P1 и P2,
то есть ![]() ,
а
,
а ![]() ,
причём атомарные формулы P1 и P2 являются
унифицируемыми наиболее общим унификатором σ.
В этом случае резольвентой
предложений C1 и C2 является
предложение
,
причём атомарные формулы P1 и P2 являются
унифицируемыми наиболее общим унификатором σ.
В этом случае резольвентой
предложений C1 и C2 является
предложение ![]() ,
полученное из предложения
применением
унификатора σ. [
правила
построения формул логики высказываний
1)Элементарное
высказывание (буква)
является формулой нулевого уровня. Если
элементарное высказывание всегда
верно, мы будем его обозначать буквой И,
а если оно всегда неверно, — буквой Л.
Тогда формулы первого уровня — это
элементарные высказывания, к которым
применена только одна логическая связка.
2)Пусть
Ф1 и Ф2 — формулы ненулевого уровня.
Тогда
записи (¬(Ф1)), ((Ф1)&(Ф2)), ((Ф1)V(Ф2)), ((Ф1)->(Ф2)), ((Ф1)~(Ф2)) также
являются формулами. Если же одна из
формул Ф1 и Ф2 ,
к которым применяется логическая связка,
имеет нулевой уровень, то она в скобки
не заключается.\\\\\\\Теперь, зная
буквы-элементарные высказывания, мы
никогда не ошибёмся, определяя, является
ли формулой запись, содержащая эти
буквы, скобки и символы связок, то есть
правильно ли построено сложное
высказывание. В процессе подобного
опознавания мы выделяем части формулы,
то есть более короткие формулы, из
которых на каждом этапе строится более
длинная формула с применением одной
связки. Самыми простыми частями формулы
являются, разумеется, элементарные
высказывания. Значит, логический анализ
формулы сводится к выделению всех её
частей.Пример
Пусть элементарными высказываниями
являются А, В, С.
Записи¬
A^BC и (B)V(ВVA->C)
c формальной точки зрения не являются
формулами, так как мы натыкаемся при их
разборе на нарушение правил построения
формул. А записи(¬
A)^(BVC) и BV((ВVA)->C)
вполне соответствуют требованиям
построения формулы\\\\\Соглашения
о скобках
Поскольку
в построенных по определению формулах
оказывается слишком много скобок, иногда
и не обязательных для однозначного
понимания формулы, математики приняли
соглашения
о скобках,
по которым некоторые из скобок можно
опускать. Записи с опущенными скобками
восстанавливаются так:1)Если
опущены внешние скобки, то они
восстанавливаются.2)Если
рядом стоят две конъюнкции или дизъюнкции (например,
,
полученное из предложения
применением
унификатора σ. [
правила
построения формул логики высказываний
1)Элементарное
высказывание (буква)
является формулой нулевого уровня. Если
элементарное высказывание всегда
верно, мы будем его обозначать буквой И,
а если оно всегда неверно, — буквой Л.
Тогда формулы первого уровня — это
элементарные высказывания, к которым
применена только одна логическая связка.
2)Пусть
Ф1 и Ф2 — формулы ненулевого уровня.
Тогда
записи (¬(Ф1)), ((Ф1)&(Ф2)), ((Ф1)V(Ф2)), ((Ф1)->(Ф2)), ((Ф1)~(Ф2)) также
являются формулами. Если же одна из
формул Ф1 и Ф2 ,
к которым применяется логическая связка,
имеет нулевой уровень, то она в скобки
не заключается.\\\\\\\Теперь, зная
буквы-элементарные высказывания, мы
никогда не ошибёмся, определяя, является
ли формулой запись, содержащая эти
буквы, скобки и символы связок, то есть
правильно ли построено сложное
высказывание. В процессе подобного
опознавания мы выделяем части формулы,
то есть более короткие формулы, из
которых на каждом этапе строится более
длинная формула с применением одной
связки. Самыми простыми частями формулы
являются, разумеется, элементарные
высказывания. Значит, логический анализ
формулы сводится к выделению всех её
частей.Пример
Пусть элементарными высказываниями
являются А, В, С.
Записи¬
A^BC и (B)V(ВVA->C)
c формальной точки зрения не являются
формулами, так как мы натыкаемся при их
разборе на нарушение правил построения
формул. А записи(¬
A)^(BVC) и BV((ВVA)->C)
вполне соответствуют требованиям
построения формулы\\\\\Соглашения
о скобках
Поскольку
в построенных по определению формулах
оказывается слишком много скобок, иногда
и не обязательных для однозначного
понимания формулы, математики приняли
соглашения
о скобках,
по которым некоторые из скобок можно
опускать. Записи с опущенными скобками
восстанавливаются так:1)Если
опущены внешние скобки, то они
восстанавливаются.2)Если
рядом стоят две конъюнкции или дизъюнкции (например, ![]() ),
то в скобки заключается сначала самая
левая часть (т.е. две подформулы со
связкой между ними). 3)Если
рядом стоят разные связки, то скобки
расставляются согласно приоритетам:
),
то в скобки заключается сначала самая
левая часть (т.е. две подформулы со
связкой между ними). 3)Если
рядом стоят разные связки, то скобки
расставляются согласно приоритетам: ![]() и
и ![]() (от
высшего к низшему) Например:
запись
(от
высшего к низшему) Например:
запись
![]() означает
формулу
означает
формулу ![]() ,
а её длина равна 12.]\\\\Истинностное
значениеОценкой пропозициональных
переменных называется функция из множества всех
пропозициональных переменных в множество
{0, 1}. Основной задачей логики высказываний
является установление истинностного
значения формулы,
если дана оценка. Истинностное значение
формулы в таком случае определяется
индуктивно с использованием таблиц
истинности связок.\\\\Оценка
отрицания
,
а её длина равна 12.]\\\\Истинностное
значениеОценкой пропозициональных
переменных называется функция из множества всех
пропозициональных переменных в множество
{0, 1}. Основной задачей логики высказываний
является установление истинностного
значения формулы,
если дана оценка. Истинностное значение
формулы в таком случае определяется
индуктивно с использованием таблиц
истинности связок.\\\\Оценка
отрицания ![]() задаётся
таблицей:
задаётся
таблицей:
|
|
|
|
|
|
Значение
двуместных логических
связок
(импликация), ![]() (дизъюнкция)
и
(дизъюнкция)
и ![]() (конъюнкция)
определются так:
(конъюнкция)
определются так:
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных.
Законы де Моргана: Законы поглощения:
1) ![]() ;
Закон
контрапозиции:
;
Закон
контрапозиции:
![]()
2) ![]() ;
;
![]()
![]()
;Законы дистрибутивности:
1) ![]() ;
;
2) ![]() Одним
из возможных вариантов) аксиоматизации
логики высказываний является следующая
система аксиом:
Одним
из возможных вариантов) аксиоматизации
логики высказываний является следующая
система аксиом:
![]() ;
;
![]()
![]()
;
![]()
![]()
![]()
![]()
;
![]()
![]()
;
![]()
![]() вместе с единственным правилом:
вместе с единственным правилом:
![]() (Modus
ponens)
Теорема корректности исчисления
высказываний утверждает, что все
перечисленные выше аксиомы
являются тавтологиями,
а с помощью правила modus ponens из истинных
высказываний можно получить только
истинные.Ввсе
остальные тавтологии
можно получить из аксиом с помощью
правила вывода
(Modus
ponens)
Теорема корректности исчисления
высказываний утверждает, что все
перечисленные выше аксиомы
являются тавтологиями,
а с помощью правила modus ponens из истинных
высказываний можно получить только
истинные.Ввсе
остальные тавтологии
можно получить из аксиом с помощью
правила вывода
