Множества, функции, отношения. Операции над множествами. Соответствия и их свойства. Общее понятие отношения. Бинарные отношения и их свойства. Отношение порядка.
Множество – любая определенная совокупность объектов. Множество, не содердащее элементов называется пустым. Множество, содержащее все элементы, находящиеся в рассмотрении называется универсумом.
Примеры: множество натуральных чисел, множество простых чисел, множество вещественных чисел, множество всех решений уравнения и т.д.
Задание
множеств: - перечисление элементов
-
только для конечных множеств-характеристический
предикат
-
описание свойств элементов, принадлежащих
множеству-
порождающая процедура
,
рекурсивное
определение элементов, образование
множеств из других множеств
Задание
множества характеристическим предикатом
может привести к противоречиям. Рассмотрим
множество всех множеств, не содержащих
себя в качестве элемента: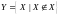
.
Если множество Y
существует, то мы должны иметь возможность
ответить на следующий вопрос:
?
Пусть
,
тогда
.
Пусть
,
тогда
.
Получается неустранимое логическое
противоречие, которое называется
парадокс
Рассела.
Множество
называется подмножеством множества
,
если все элементы множества
принадлежат множеству
:
Если
при этом множества не совпадают, то
называют собственным
подмножеством
Совокупность
всех подмножеств некоторого множества
называется его булеаном
или множеством-степенью
и
обозначается
.
Мощность множества – количество элементов в нем.
Основные операции над множествами:
-объединение
-пересечение
-разность
-симметрическая
разность(кольцевая сумма)
-дополнение
Свойства операций над множеством:
-идемпотентность
-коммутативность
-ассоциативность
-дистрибутивность
-поглощение:
-свойства нуля и единицы:
-закон двойного отрицания = инволютивность :
-законы де Моргана
-выражение для разности:
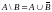
Множество непустых подмножеств называется покрытием множества А, если их объединение дает множество А. Такое множество подмножеств называется разбиением множества А, если пересечение любых пар таких подмножеств пусто.
n-местным
отношением, или n-местным
предикатом P
на множествах
называется
любое подмножество прямого произведение
.
Другими
словами, элементы
,
где
связаны соотношением P,
тогда и только тогда, когда
.
При n=1 отношение называется унарным, или свойством. Наиболее часто встречаются двухместные отношения. Они называются бинарными отношениями или соответствиями.
Бинарные отношения и их свойства.
Областью
определения
отношения называется
Областью
значений о
отношения называется
Произведение (композиция) отношений обладает свойством ассоциативности.
Область
определения функции из А в В - все
множество А, область значений –
подмножество множества B.
Если же область определения отношение
– подмножество функции, то такое
отношение называется частичной функцией.
Инъекция – это функция из А в В ,
одновременно являющаяся частичной
функцией из В в А. Сюрьекция – функция,
для которой область значений совпадает
с множеством В.
Соответствия
и их свойства. Соответствием
между множествами A
и B
называется подмножество
.
Если
,
то говорят, что b
соответствует
при соответствии
.
Соответствие – это бинарное отношение. Аналогично любому бинарному отношению, соответствие может быть сюрьективным, биективным, инъективным. Проекция соответствия на первую ось – область определения, на вторую – область значения.