МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Національний авіаційний університет

Кафедра засобів захисту інформації

Реферат

на тему:

«Вимірювання напруженості електричного і магнітного поля»

Виконав:

Студент 321 групи

Шматько М. В.

Перевірив:

Пепа Ю. В.

Київ 2013

Методи вимірювання електричних полів в атмосфері можна поділити на три класи: І. Оцінка напруженості поля за різницею потенціалів між електродами, що перебувають у полі. ІІ. Вимірювання величини заряду, що індуктується полем на поверхні провідника: Е= πσ, де σ- поверхнева густина заряду. ІІІ. Аналіз впливу поля на рух електронів або іонів.

Магнітне поле - силове поле, яке діє на електричний заряд, що рухається, та на тіла, що мають магнітні властивості. Магнітне поле характеризується вектором магнітної індукції В і напруженістю магнітного поля Н.

Відомо, що електростатичне поле є наслідком наявності нерухомого постійного електричного заряду та виявляється за силовим впливом на пробний заряд. Джерелом магнітостатичного поля є постійний електричний струм. Визначається воно за силовою дією на рухомий електричний заряд. Обидва поля будуть залишатися статичними до тих пір, доки параметри їх джерел залишаються незалежними від часу. Розглянемо, що ж буде відбуватись при зміні їх з часом, яким закономірностям будуть підпорядковуватися процеси при введенні параметра "час". Перед тим, як розглянути їх динаміку полів, тобто власно електродинаміку, необхідно згадати основні закони, яким підлягають електро- і магнітостатичні поля, що були досліджені у попередньому циклі лекцій.

Для знаходження характеристик електростатичного поля згідно з заданими значеннями електричних зарядів використають рівняння Гауса–Остроградського в інтегральній формі:

, (1)

відповідно до якого потік вектора електричної індукції через довільну замкнену поверхню дорівнює алгебраїчній сумі електричних зарядів, які утримуються в неї.

Знайти значення електричного заряду в конкретній точці за характеристиками електростатичного поля дозволяє рівняння Гауса–Остроградського в диференційній формі:

, (2)

тобто дивергенція вектора дорівнює об’ємній густині заряду .

Теорема Гауса–Остроградського зв’язує поверхневий та об’ємний інтеграли:

(3)

і дозволяє змінювати порядок інтегрування, що значно полегшує розв’язування деяких задач.

Напруженість електростатичного поля визначається зміною потенціалу в просторі:

.

Пряма задача електростатики у загальному вигляді розв’язується застосуванням рівняння Пуассона:

.

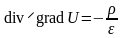Його розв’язок якого має вид:

,

де – відстань від елемента об’єму до точки спостереження.

Розв’язок прямої задачі магнітостатики забезпечується законом повного струму в інтегральній формі:

, (4)

тобто циркуляція вектора по замкненому контуру дорівнює алгебраїчній сумі охоплених ним струмів. Для розв’язування зворотної задачі магнітостатики служить закон повного струму в диференційній формі:

, (5)

у відповідності з яким густина струму в конкретній точці визначається рото­ром вектора .

Потік вектора магнітної індукції через замкнену поверхню дорівнює алгебраїчній сумі магнітних зарядів, що містяться в цій поверхні, але оскільки вони парні, то

.

У диференційній формі цей вираз записується так:

.

Теорема Стокса:

, (6)

яка дозволяє змінювати порядок інтегрування, свідчить про те, що циркуляція вектора по замкненому контуру дорівнює потоку його ротора через поверхню, обмежену цим контуром.

Тепер від статики перейдемо до динаміки і введемо параметри "часу". Оскільки заряд первинний по відношенню до здійсненного ним поля, подивимося, що відбувається при зміні електричного заряду з часом.

Розглянемо об’єм , обмежений замкненою поверхнею , в середині якого є заряди. Нехай в момент часу кількість зарядів дорівнюва­ла , а в момент часу – дорівнює . На основі закону збереження мате­рії можна зробити висновок: якщо зарядів стало менше, то вони не зникли безслідно, а, залишивши межі об'єму , утворили потік електричних зарядів, тобто елект­ричний струм. При цьому зміну зарядів подамо у вигляді частинної похідної в часі.

Тоді електричний струм визначається виразом

, (7)

а струм через одиницю поверхні – густина електричного струму:

. (8)

Із співвідношення (3.8) знайдемо електричний струм:

. (9)

Тут права частина характеризує потік електричних зарядів крізь замкнену поверхню . На основі виразів (2.1) та (2.3) отримаємо співвідношення:

,

яке відображає інтегральну форму закону збереження заряду: будь-яка зміна зарядів з часом у середині деякого об’єму супроводжується виходом рівної кількості зарядів через поверхню, яка обмежує цей об’єм.

Тепер слід з’ясувати, що відбувається в конкретній точці об’єму при зміні заряду. Користуючись теоремою Гауса–Остроградського (3.3), підвищимо порядок інтегрування :

.

Загальний заряд визначається через густину електричного заряду як .

Тоді:

.

Тут в лівій та правій частинах запису знаходяться інтеграли одного порядку. Але, якщо вони рівні, тоді рівні й підінтегральні вирази, тому отриманий вираз можна переписати у наступному вигляді:

. (10)

Одержане співвідношення виражає закон збереження електричного заряду, наданий в диференційній формі: дивергенція густини струму дорівнює швидкості зміни заряду в конкретній точці простору, взятій із зворотним знаком.

Припустимо тепер, що у співвідношенні (11) = const. Тоді

. (3.11)

Це означає, що сума струмів у точці їх сходження дорівнює нулю. Очевидно, що звісний з теорії електричних кіл перший закон Кірхгофа є наслідком співвідношення (3.11).

Кількість вільних зарядів в одиниці об’єму характеризує провідну властивість середовища. Тому означений ними електричній струм називається струмом провідності . Відношення (3.10) свідчить про те, що лінії густини струму провідності починаються і закінчуються в точках із змінною густиною зарядів. Співвідношення (3.11) вказує на вихровий характер постійних струмів і свідчить про те, що для їх існування електричне коло повинне бути безперервним. Кола змінного струму, як свідчить вираз (3.11), припускають розрив кондуктивних зв’язків, але в цьому випадку крім струмів провідності повинні існувати й струми іншої фізичної природи, які збуджуються тими самими електричними зарядами.

Поки що ми розглядали електричні і магнітні поля, які не зв’язані одне з іншим. Проте такий зв’язок має бути, бо першоджерелами як електричних (3.1), так і магнітних полів (3.4) є електричні заряди. Очевидно, характеристики полів та їх джерел взаємозв’язані системою рівнянь. Цих рівнянь шість, оскільки у тривимірному просторі кожний з невідомих векторів і задається трьома своїми проекціями. Ці рівняння називаються рівняннями Максвела. Розглянемо кожне з них.

Рівняння Максвела

Перепишемо рівняння (10) з урахуванням (2):

. (11)

Величину , яка згідно з виразом (11) має розмірність густини струму, визначимо символом та назвемо густиною струму зміщення (густина струму в діелектриках). Об’єднаємо ліву та праву частину співвідношення (3.11) та представимо його як

. (12)

Відомо, що, якщо дивергенція будь-якого вектора дорівнює нулю, то існує новий вектор, ротор якого буде дорівнювати початковому вектору, тобто вектору . Очевидно, що цей новий вектор повинен мати розмірність вектора напруженості магнітного поля . Тому із співвідношення (4) випливає, що

. (13)

Співвідношення (13) – це перше рівняння Максвелла, записане в диференціній формі. У ньому – густина струму зміщення, а – густина струму провідності (це закон Ома в диференційній формі), – питома провідність середовища. Очевидно, що співвідношення (5) – окремий випадок рівняння (13), відомого як узагальнений закон повного струму.

Нехай = 0, тоді відношення (3.13) набуває вигляду:

, (14)

тобто струм зміщення, як і струм провідності, породжує вихрове магнітне поле. Знак рівності в (14) свідчить про однакову напрямленість та вектора . Оскільки вектор rot є перпендикулярним вектору за визначенням, то вектори та теж взаємно перпендикулярні.

Перше рівняння Максвела в диференційній формі зв’язує струм в конкретній точці з проекціями . Сам вектор може бути виражений через повний струм шляхом інтегрування відношення (13) по площині замкненої поверхні :

. (15)

В лівій частині (15) за теоремою Стокса (36) понизимо порядок інтегрування. Тоді (15) матиме вигляд

.

Цей вираз є інтегральною формою першого надання рівняння Максвела: циркуляція по замкненому контуру дорівнює повному струму, який оточується цим контуром. Струми провідності та струми зміщення є повноправними джерелами вихрового магнітного поля.

З курсу фізики відомий закон електромагнітної індукції – закон Фарадея: електрорушійна сила в замкненому провідному контурі дорівнює швидкості зміни магнітного потоку, але з протилежним знаком:

, (16)

тобто ЕРС протидіє зміні магнітного потоку

.

Максвел узагальнив цей закон для будь-якого контуру, а не тільки провідного.

За визначенням ЕРС – це робота по переміщенню заряду з однієї точки в іншу через джерело збудження. Але цю роботу можна розглядати як різницю потенціалів, тобто ЕРС можна зв’язати з характеристиками електричного поля.

У відношенні (17) подамо ЕРС у вигляді роботи, тобто циркуляція вектора по замкненому контуру :

,

або, розкриваючи зміст лівої частини як магнітного потоку

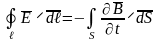. (17)

Для лівої частини (17) застосуємо теорему Стокса:

,

тоді

,

або

. (18)

Відношення (3.18) є другим рівнянням Максвела, що записане в диференційній формі: електричне поле, утворене магнітним полем, яке змінюється з часом, має вихровий характер.

Рівняння Максвела описують електромагнітне поле як форму існування матерії.

Перше рівняння – узагальнений закон повного струму в диференційній формі:

або в інтегральній: 

зв’язує електричні та магнітні поля, що змінюються з часом.

Друге рівняння – узагальнений закон електромагнітної індукції в диференційній формі

,

а в інтегральній формі

,

де - магнітний потік, що визначає зміну електричного поля в просторі через зміну магнітного поля з часом.

Третє рівняння – це рівність Гауса–Остроградського в диференційній формі:

та в інтегральній формі:

,

яке свідчить про те, що джерелом безвихрового (потенціального) електричного поля є електричні заряди.

Четверте рівняння в диференційній формі:

або в інтегральній формі: 

,

свідчить про відсутність джерел безвихрового магнітного поля, тобто вільних магнітних зарядів.

П’яте та шосте рівняння:

,

є матеріальними, тобто зв’язують між собою характеристики поля та параметри середовища, в якому це поле існує.

При аналізі електромагнітних явищ зручною може бути комплексна форма подання рівнянь Максвела, яка дозволяє формально звільнитися від параметра "час".