9. Общее уравнение и инварианты поверхности 2-ого порядка
Пусть поверхность
S
задана в декартовой системе координат
уравнением:
Если хотя бы один
из коэффициентов
отличен от нуля, то поверхность S
называют поверхностью
второго
порядка.
Теорема
1. Для произвольной поверхности второго
порядка S
существует такая декартова прямоугольная
система координат
,
что в этой системе поверхность S
имеет уравнение одного из следующих
канонических видов:
1)
- эллипсоид,
2)
- мнимый эллипсоид,
3)
- однополостный гиперболоид,
4)
- двуполостный
гиперболоид
5)
- конус,
6)
- мнимый конус (точка),
7)
- эллиптический параболоид,
8)
- гиперболический
параболоид,
9)
- эллиптический
цилиндр,
10)
- мнимый
эллиптический цилиндр,
11)
-
две мнимые пересекающиеся плоскости,
12) - гиперболический цилиндр,
13) - две пересекающиеся плоскости,
14)
- параболический
цилиндр,
15)
- две параллельные плоскости,
16)
- две мнимые параллельные
плоскости,
17) - две совпадающие плоскости.
В
этих уравнениях
- положительные параметры.
Функция
называется квадратичной
формой,
соответствующей уравнению (3.1).
Характеристическим
уравнением
квадратичной формы
называется уравнение
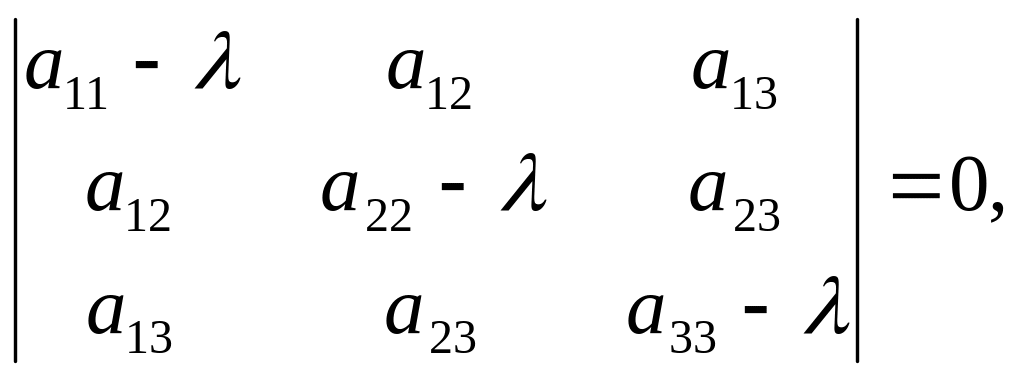(3.2)
а корни
уравнения (3.2) называются характеристическими
числами
квадратичной формы
.
В общем случае характеристическое уравнение (3.2) записывается в виде
(3.3)
где
(3.4)
(3.5)
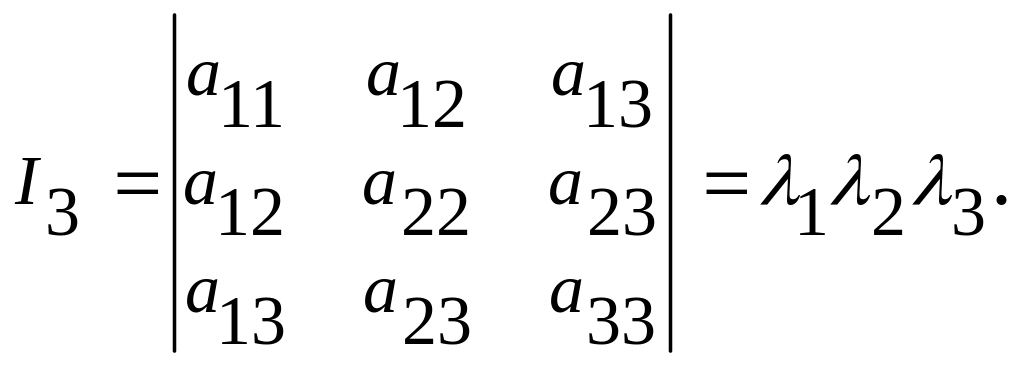(3.6)
Обозначим
,
(3.7)
(3.8)
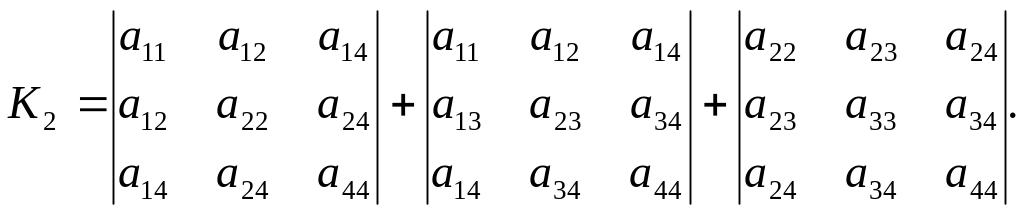(3.9)
Значения
не меняются при переходе от одной
декартовой прямоугольной системы
координат к другой, полученной в
результате поворота осей координат и
переноса начала координат, то есть
являются
инвариантами
поверхности S
относительно поворота осей координат
и переноса начала.
Значения
и
являются
инвариантами поверхности S
только относительно поворота осей
координат
(их часто называют семиинвариантами).
Замечание
1. Для
вычисления инварианта
можно использовать формулу
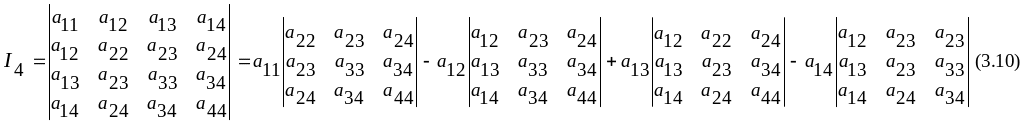
Теорема 2. Для
любой поверхности второго порядка S
существуют углы
и числа
такие, что с помощью преобразования
поворота осей и переноса начала координат
(3.11)
уравнение (3.1) приводится к одному из следующих пяти видов (групп):
если
(3.12)
,
если
(3.13)
если
(3.14)
если
(3.15)
если
(3.16)
где
- определены формулами (3.4)-(3.9) соответственно,
а
- корни характеристического уравнения
(3.3).