7. Поверхности второго порядка

7.1. Эллипсоид Эллипсоид (рис. 3.1) имеет каноническое уравнение , (3.19) где - полуоси. Также это уравнение можно записать в виде .

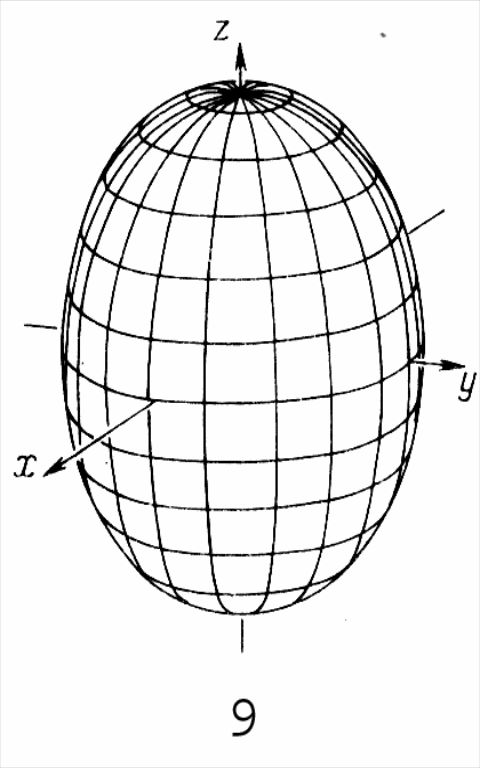
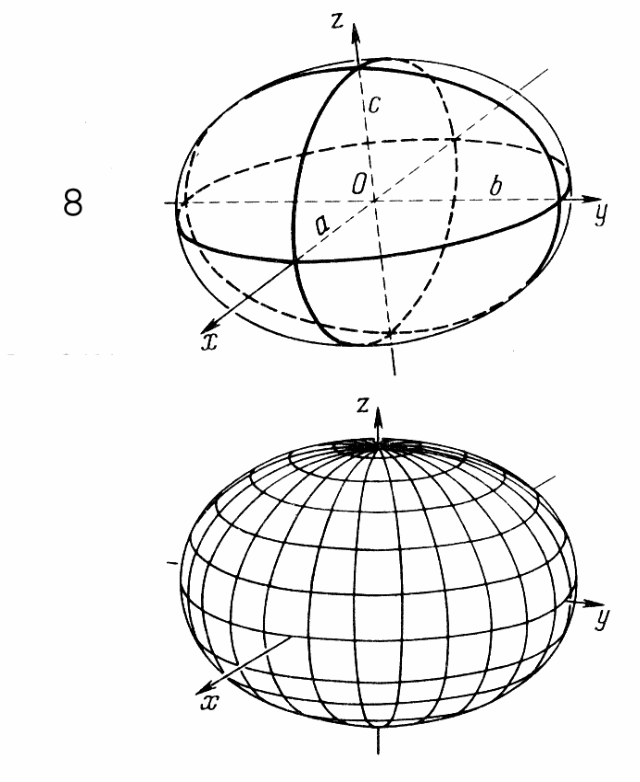
Рис. 3.1. Рис. 3.2.

Если , то имеем сплющенный эллипсоид вращения, получающийся при вращении вокруг малой оси эллипса , лежащего в плоскости Оxz. Если , имеем вытянутый эллипсоид вращения, который получается при вращении лежащего в плоскости Oxz, эллипса вокруг его большой оси (рис. 3.2). При имеем сферу (шар) .

Сечение эллипсоида любой плоскостью есть эллипс (в частном случае – круг). Объём эллипсоида равен

Как уже было указано, частным случаем эллипсоида является шар или сфера, уравнение шара получается из уравнений эллипсоида при a=b=c, объём сферы равен .

7.2. Однополосный гиперболоид

Однополосный гиперболоид (рис. 3.3) имеет каноническое уравнение

, (3.20)

где - действительные полуоси, c – мнимая полуось (О прямолинейных образующих).

Так же это уравнение можно записать в виде .

Прямолинейной образующей поверхности называется прямая линия, целиком и полностью лежащая на данной поверхности; например, прямолинейные образующие конической или цилиндрической поверхности.

Однополосный гиперболоид (рис. 3.4) имеет два семейства прямолинейных образующих:

I .

II .

где u и - произвольные величины.

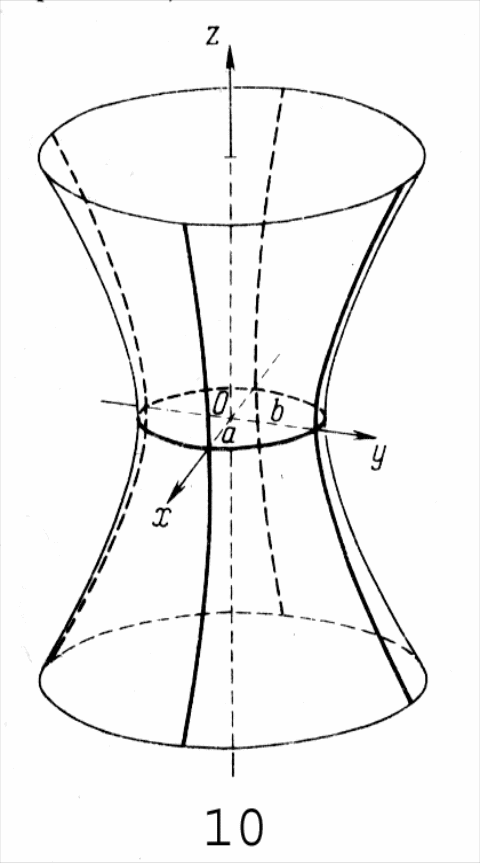
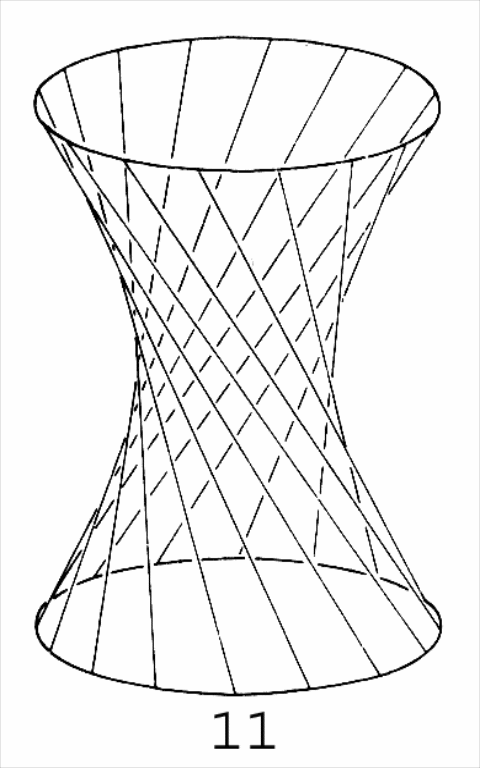
Рис. 3.3. Рис. 3.4.

Через каждую точку поверхности проходят две прямые: по одной образующей из каждого семейства (на рис. 3.4 показано лишь одно семейство прямых, «закрученных» по часовой стрелке, если смотреть на гиперболоид сверху). Замечательное свойство поверхности однополостного гиперболоида – иметь прямолинейные образующие использовал инженер Шухов в начале XX-ого века, при постройке башни на улице Шаболовка в Москве. Эта башня сохранена до настоящего времени как инженерный и архитектурный памятник.

7 .3. Двуполостный гиперболоид

Двуполостный гиперболоид (рис. 3.5) имеет каноническое уравнение , где с – действительная полуось, а a и b – мнимые полуоси.

Для обоих гиперболоидов сечения, параллельные оси z – гиперболы (для однополостного гиперболоида может быть пара пересекающихся прямых); сечения, параллельные плоскости Oxy – эллипсы.

Если a=b, то гиперболоид может быть получен вращением гиперболы с полуосями a и c, вокруг оси z: мнимой – в случае однополостного и действительной – в случае двуполостного гиперболоида.

Рис. 3.5.

7.4. Конус

Конус (рис. 3.6), каноническое уравнение: ( ). Имеет вершину в начале координат; за его направляющую кривую может быть взят эллипс с полуосями a и b, плоскость которого перпендикулярна оси z, и находится на расстоянии от начала координат.

Этот конус является асимптотическим для обоих гиперболоидов т.е. каждая из его образующих при удалении в бесконечность неограниченно приближается к обоим гиперболоидам (рис. 3.7). Если a=b, то имеем прямой круговой конус.

Рис. 3.6. Рис. 3.7.