3. Классификация кривых второго порядка
В
зависимости от значения инварианта
принята следующая классификация кривых
второго порядка. Кривая второго порядка
Г, заданная уравнением (2.1), называется
центральной, если
.
Центральная
кривая Г называется кривой эллиптического
типа, если
.
Центральная
кривая Г называется кривой гиперболического
типа, если
.
Центром
кривой второго порядка Г называется
такая точка плоскости, по отношению к
которой точки этой кривой расположены
симметрично парами. Точка
является центром кривой второго порядка,
определяемой уравнением (2.1), в том и
только том случае, когда ее координаты
удовлетворяют уравнениям:
(3.1)
Определитель
этой системы равен
.
Если
,
то система имеет единственное решение.
В этом случае координаты центра могут
быть определены по формулам :
(3.2)
В
случае
кривую Г называют кривой параболического
типа.
Из теорем 1 и 2 получается следующая классификация кривых второго порядка с помощью инвариантов:
1)
эллипс
2)
мнимый эллипс
3)
две мнимые пересекающиеся прямые (точка)
4)
гипербола 
5)
две пересекающиеся прямые 
(3.3)
6)
парабола 
7)
две параллельные прямые 
8)
две мнимые параллельные прямые 
9)
две совпадающие прямые 
В
прилагаемой схеме приведения кривых
второго порядка к каноническому виду
для компактности записи коэффициенты
уравнения (2.1) переобозначены следующим
образом
.
4. Расположение кривой второго порядка
Расположение
эллипса или гиперболы относительно
начальной системы координат будет
известно, если мы будем знать координаты
центра и (в случае
)
угловой коэффициент большей оси для
эллипса и вещественной оси для гиперболы.
Координаты центра
находятся из системы уравнений (3.1).
Если линия – эллипс и - меньший по абсолютной величине корень характеристического уравнения, то формула
(4.1)
Если уравнение (1.1) определяет гиперболу, и если - корень характеристического уравнения, знак которого совпадает со знаком , то формула
(4.2)
дает угловой коэффициент вещественной оси гиперболы.
Расположение параболы относительно начальной системы координат будет известна, если мы будем знать вершину параболы, вектор, направленный по оси в сторону вогнутости, и параметр. Вершина параболы определяется при решении уравнения оси параболы
(4.3)
или
(4.3')
совместно с уравнением параболы (2.1). Вектор
(4.4)
параллелен оси параболы и направлен в сторону ее вогнутости.
Параметр параболы определяется по формуле
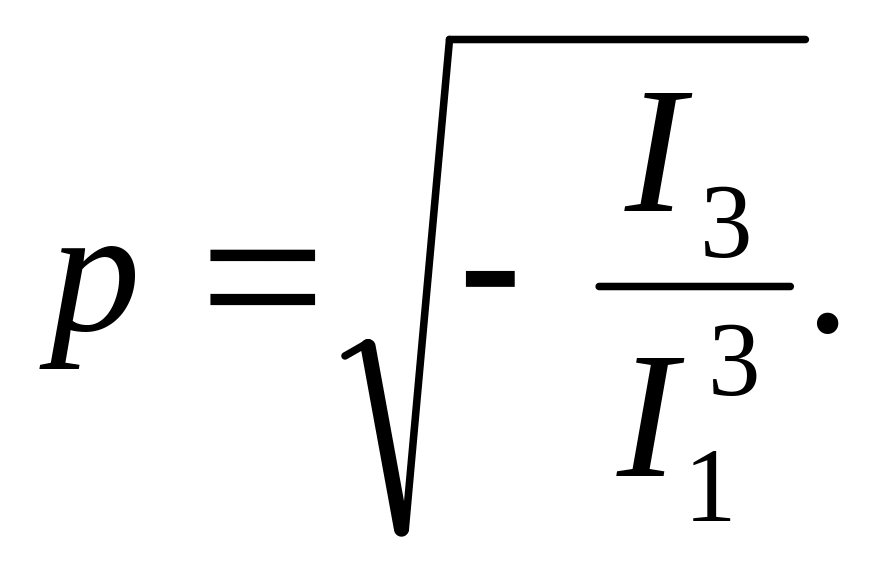(4.5)
Приведение общего уравнения кривой второго порядка к каноническому виду
Если кривая Г задана в декартовой прямоугольной системе координат уравнением (2.1), то, применяя преобразования поворота осей координат и переноса начала координат можно привести уравнение к каноническому виду.
Преобразование коэффициентов при параллельном переносе
Пусть
дано уравнение (2.1), определяющее кривую
второго порядка Г. Совершаем параллельный
поворот начала координат в точку
.
При этом координаты x,
y
произвольной точки плоскости М
в системе координат
и координаты
в новой системе координат
связаны соотношениями:
(
5.1)
Подставляя выражения (1.23) в уравнение (2.1), получим уравнение кривой в новой системе координат
, (5.2)
где
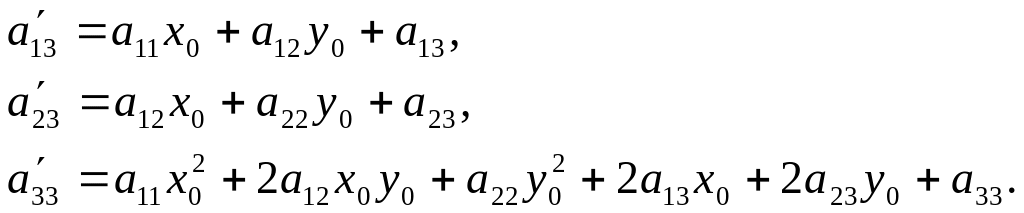(5.3)
Отметим, что при
параллельном переносе начала координат
старшие коэффициенты
не изменяются, а коэффициенты
и свободный член
преобразуются по формулам (1.25).
Предположим теперь, что уравнение (1.1) определяет центральную кривую второго порядка ( ).
Совершим параллельный перенос начала координат в точку -центр данной кривой . Так как координаты центра удовлетворяют уравнениям
то
в новой системе координат
в уравнении (1.24) коэффициенты
равны нулю и уравнение примет вид
.
(5.4)
Преобразование коэффициентов при повороте
Пусть дано уравнение (1.1), определяющее кривую второго порядка. В случае, когда , выполним преобразование поворота осей координат на угол . При этом координаты x, y произвольной точки плоскости М в системе координат и координаты в новой системе координат связаны соотношениями:
(1.27)
Подставляя (1.27) в уравнение кривой (1.1), получим
Приведем это уравнение к виду
(1.28)
Коэффициенты уравнений (1.1) и (1.28) в системах координат и соответственно связаны соотношениями:
(1.29)
Таким
образом, при повороте осей координат
на угол
коэффициенты
преобразуются по формулам (1.29), а
свободный член
не изменяется.
Покажем,
что существует угол
такой, что в преобразованном уравнении
(1.28) коэффициент при
равен нулю. Действительно, согласно
второй из формул (1.29) условие
эквивалентно равенству
(1.30)
Следовательно, достаточно угол выбрать из условия
(1.31)
После поворота на угол , удовлетворяющий условию (1.31), уравнение (1.1) не будет содержать слагаемое с произведением , то есть в новой системе координат исходное уравнение примет вид:
(1.32)
Замечание
1. Корни
квадратного уравнения (1.31) соответствует
двум взаимно перпендикулярным направлениям
(так как по теореме Виета
).
Поэтому, выбирая
вместо
,
мы только меняем
ролями оси
и
.
Замечание
2. Значения
и
выражаются через
по формулам
(1.33)
Замечание 3. Угол можно также выбрать из условия
(1.32)
которое следует из равенства (1.30).