Московский государственный технический университет радиотехники,

электроники и автоматики (МИРЭА)

Кафедра высшей математики

Аналитическая геометрия и линейная алгебра

Н.А.Фаркова

Кривые и поверхности второго порядка

Москва

УДК 517.53

Кривые и поверхности второго порядка. Учебный материал по курсу “Аналитическая геометрия и линейная алгебра” для студентов .

Составитель Н.А.Фаркова. – Московский государственный технический университе радиотехники, электроники и автоматики (МИРЭА), 25 с .

1. Кривые второго порядка

При сечение прямого кругового двуполостного конуса плоскостями получаются кривые, называемые коническими сечениями. В восьмитомном труде «Коника» Апполоний ( около 200 г. до н.э.) предложил называть коническое сечение эллипсом, параболой или гиперболой в зависимости от того, пересекает ли плоскость все образующие лишь по одной полости конуса, параллельна ли она одной образующей, или пересекает обе его полости.

С созданием Декартом в 17 в. координатного метода стереометрическое определение конических сечений было заменено планиметрическими определениями этих кривых как множеств точек на плоскости.

1.1. Окружность

Множество точек плоскости, равноудаленных от заданной точки, называемой центром, называется окружностью.

В декартовых координатах уравнение окружности радиуса R с центром в начале координат имеет вид

(1.1)

(см. рис.1.1.а)).

Уравнение окружности радиуса R с центром в точке C (x₀, y₀)

(1.2)

(см. рис.1.1.б)).

Рис. 1.1

В параметрической форме окружность (рис.1.1, б) задается уравнениями:

здесь t – угол, образованный подвижным радиусом с положительным направлением оси Ox.

1.2 Эллипс

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.

Пусть M – точка эллипса с фокусами F₁ и F₂ . Тогда , где а – const. Если

F₁F₂ =2a, то , то есть . Выберем систему координат так, что точка О находится в середине отрезка F₁F₂ и ось направлена от F₁ к F₂.

Тогда

Отсюда получается каноническое уравнение эллипса:

(1.3)

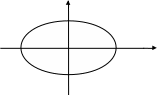
Рис. 1.2

Где Числа и называются полуосями эллипса. В случае эллипс превращается в окружность.

Форма эллипса характеризуется его эксцентриситетом так как .

Расстояния от произвольной точки эллипса до его фокусов F₁ и F₂ вычисляются по формулам

(так что ).

Директрисы эллипса имеют уравнения и соответственно. Обозначим через d₁ и d₂ расстояния от точки M до директрис и соответственно. Точка M лежит на эллипсе тогда и только тогда, когда

,

т.е. отношение расстояния от точки M до фокуса к расстоянию от этой точки до соответствующей директрисы равно эксцентриситету эллипса.

Уравнение касательной к эллипсу в точке имеет вид

(1.4)

1.3 Гипербола

Гиперболой называется множество точек плоскости, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.

Пусть M - точка гиперболы с фокусами F₁ и F_2. Тогда F₁ M- F₂M =2a, где а – const. Если F₁F₂ =2с, то , то есть .

Выберем систему координат так, что точка О находится в середине отрезка F₁F₂ и ось направлена от F₁ к F₂. Гипербола состоит из двух ветвей и в канонической системе координат имеет вид:

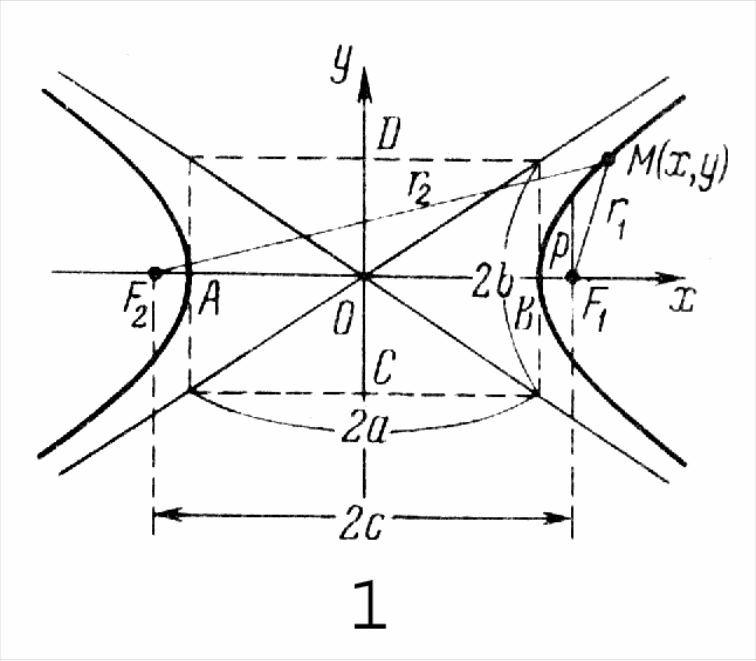
Рис. 1.3 Рис. 1.4

Вершины А и В гиперболы лежат на действительной оси и ; на мнимой оси .

Каноническое уравнение гиперболы имеет вид:

. (1.5)

Числа а и b называются полуосями гиперболы.

Оси канонической системы координат являются осями симметрии гиперболы, т.к. при замене на и на уравнение (2.5) не меняется.

Уравнения асимптот гиперболы (рис. 1.5) имеют вид : .

При а = b гиперболу называют равносторонней.

Форма гиперболы характеризуется ее эксцентриситетом так как .

Рис. 1.5 Рис. 1.6

Расстояния от произвольной точки гиперболы до ее фокусов F₁ и F₂ вычисляются по формулам

Для правой ветви ( ):

Для левой ветви ( ):

В обоих случаях .

Директрисы гиперболы имеют уравнения и . Обозначим через d₁ и d₂ расстояния от точки M до директрис и соответственно. Точка M лежит на гиперболе тогда и только тогда, когда

,

т.е. отношение расстояния от точки M до фокуса к расстоянию от этой точки до соответствующей директрисы равно эксцентриситету гиперболы.

Уравнение касательной к гиперболе в точке имеет вид