Уравнение плоскости, проходящей через две точки

Если прямая проходит через точки , , то в качестве направляющего вектора может быть выбран вектор . Точка лежит на данной прямой тогда и только тогда, когда векторы и коллинеарны. Отсюда получается уравнение:

.

Общие уравнения прямой в пространстве

Прямая может быть задана как линия пересечения двух плоскостей:

(1)

Для того, чтобы от общих уравнений (1) перейти к каноническим уравнениям прямой следует выполнить два шага.

Шаг 1. В качестве направляющего вектора выбрать вектор , где ,  нормальные векторы данных плоскостей.

Шаг 2. Найти точку ,лежащую на линии пересечения двух данных плоскостей. Для этого в уравнения (1) вместо одной из переменных следует подставить произвольное значение, а затем найти значения двух других переменных, решив полученную систему.

Пример. Написать канонические уравнения прямой

(2)

По условию , . В качестве направляющего вектора выберем . Имеем

,

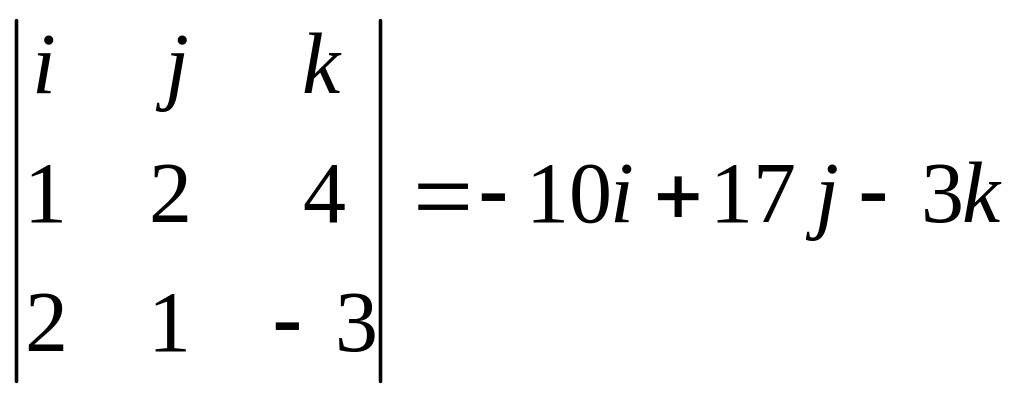т.е. . Выберем , а и найдем из системы

Решением этой системы является пара чисел . Значит, точка лежит на данной прямой и ее канонические уравнения имеют вид:

. 

Взаимное расположение прямой и плоскости

Пусть дана прямая

,

и плоскость

, .

Возможны три случая:

I. Прямая параллельна плоскости тогда и только тогда, когда векторы и ортогональны, а точка не лежит на данной плоскости:

II. Прямая лежит на плоскости тогда и только тогда, когда векторы и ортогональны и точка принадлежит плоскости:

III. Прямая пересекает плоскость тогда и только тогда, когда векторы и не ортогональны:

(1)

При условии (1) координаты точки пересечения находятся из системы

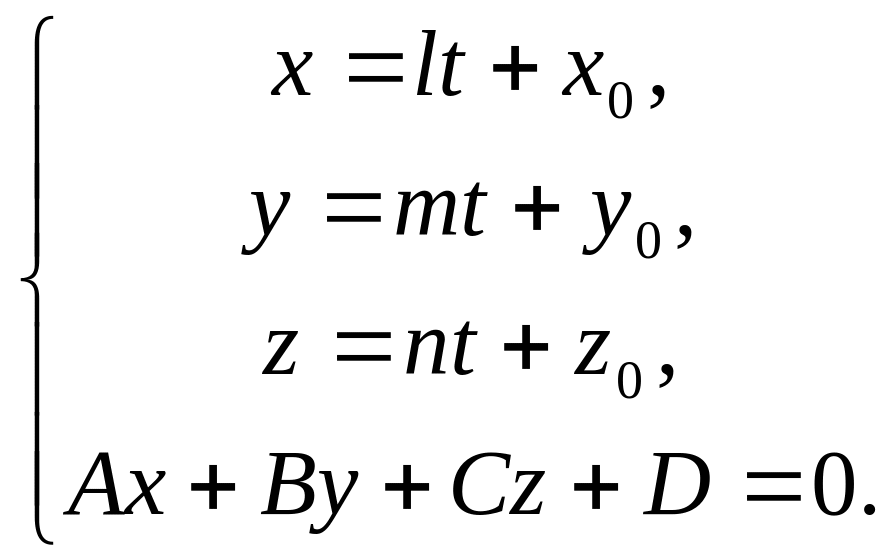(2)

Пример. Найти точку пересечения прямой

и плоскости .

В данном случае система (2) имеет вид

Подставив первые три уравнения в четвертое, получим

, .

Значит, данная прямая и плоскость пересекаются в точке .

При условии (1) иногда требуется найти угол между прямой и плоскостью. Если векторы и коллинеарны, то есть

, (3)

то угол равен 90°. Если условие (3) не выполнено, то обозначим через угол между и . Векторы и можно выбрать так, что угол между прямой и плоскостью связан с углом равенством . Тогда

и, значит,

. (4)

Формула (4) верна и в том случае, когда прямая лежит на плоскости.

Упражнение. Найти расстояние от точки до прямой .

Способ 1. Пусть – проекция точки на данную прямую. Если через эту точку провести плоскость перпендикулярно данной прямой, то точка совпадет с точкой пересечения этой плоскости с данной прямой, а искомое . Вектор ортогонален рассматриваемой плоскости. А точка лежит на этой плоскости. Поэтому уравнение плоскости имеет вид

или

.

Координаты точки найдем из системы

Следовательно, точка имеет координаты , , . Поэтому и .

Способ 2. Площадь параллелограмма, построенного на векторах и ,

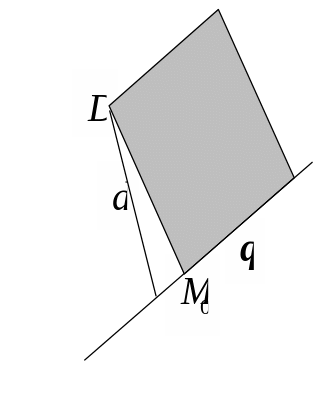
совпадает с каждой из следующих величин: и . Следовательно,

. (5)

Имеем: и

.

Поэтому , и, по формуле (5),

.