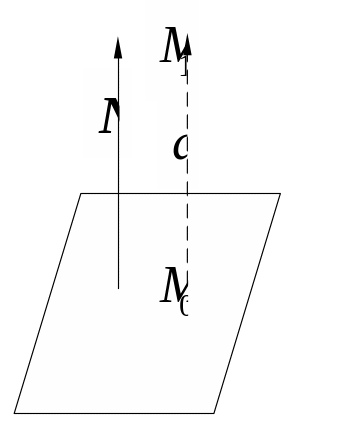
Расстояние от точки до плоскости

Пусть дана плоскость

(1)

и пусть точка не принадлежит этой плоскости. Обозначим через ортогональную проекцию точки на данную плоскость.

Векторы и коллинеарны, так как они перпендикулярны одной и той же плоскости. Если  угол между и то либо , либо . В обоих случаях . Расстояние от точки до данной плоскости совпадает с модулем вектора : . Поэтому из формулы получаем

.

Здесь

.

Таким образом, расстояние от точки до плоскости вычисляется по формуле

.

Взаимное расположение двух плоскостей

Пусть даны две (различные) плоскости

, и , .

Возможны три случая.

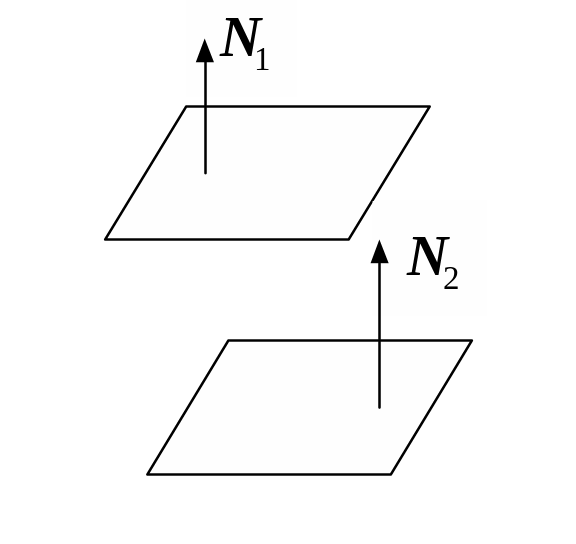
I. Плоскости параллельны. В этом случае векторы и коллинеарны и выполнены равенства:

.

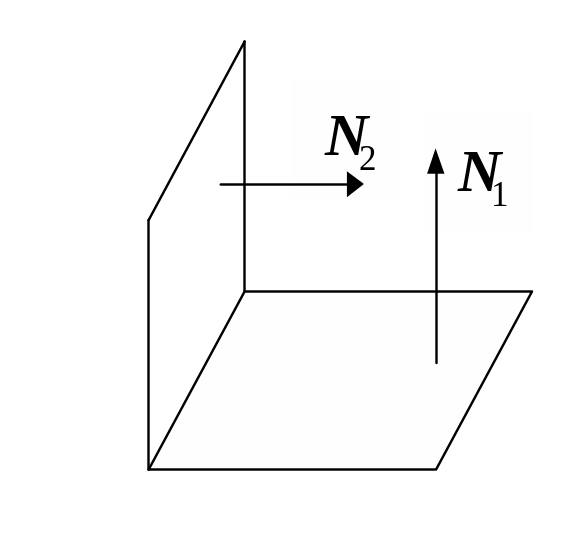
II. Плоскости перпендикулярны. Тогда векторы и ортогональны, то есть или

.

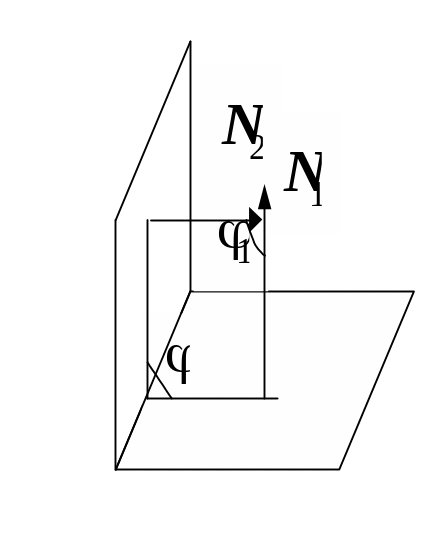2. П лоскости пересекаются, но не перпендикулярны.

Обозначим через линейный угол двугранного угла между данными плоскостями. Нормальные векторы и можно выбрать так, что , где  угол между и . Тогда угол находится из равенств

.

Уравнение плоскости, проходящей через три точки

Пусть точки , , не лежат на одной прямой.

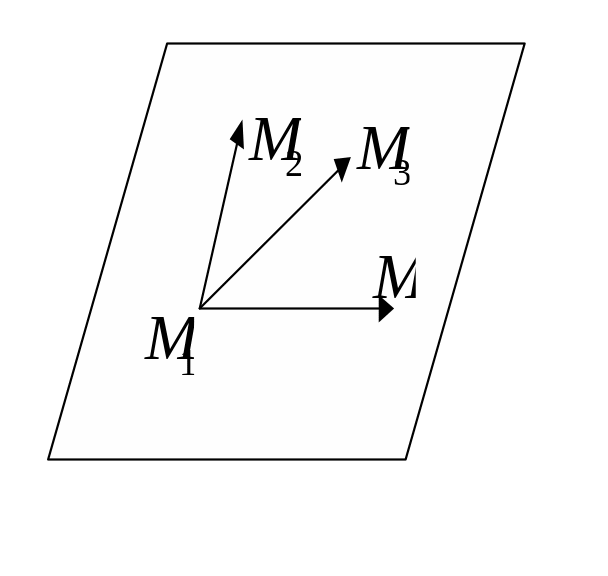
Точка лежит в одной плоскости с точками , , тогда и только тогда, когда векторы , , компланарны, то есть когда выполнено условие:

.

Отсюда получаем уравнение:

.

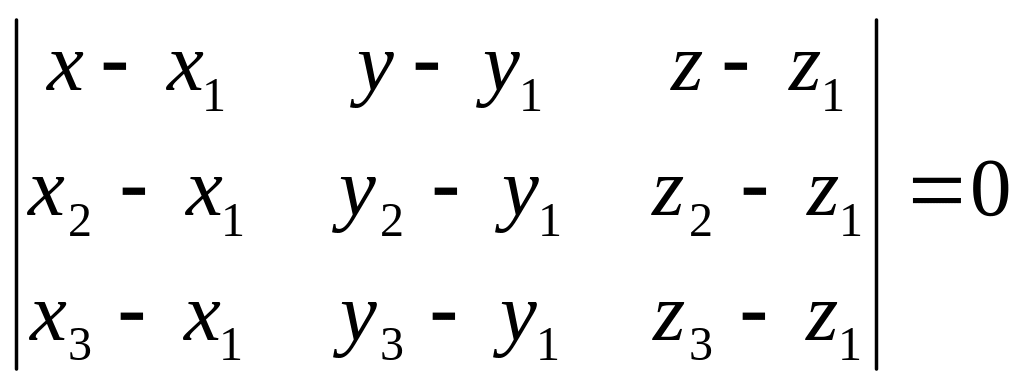Пример. Для точек , , имеем

,

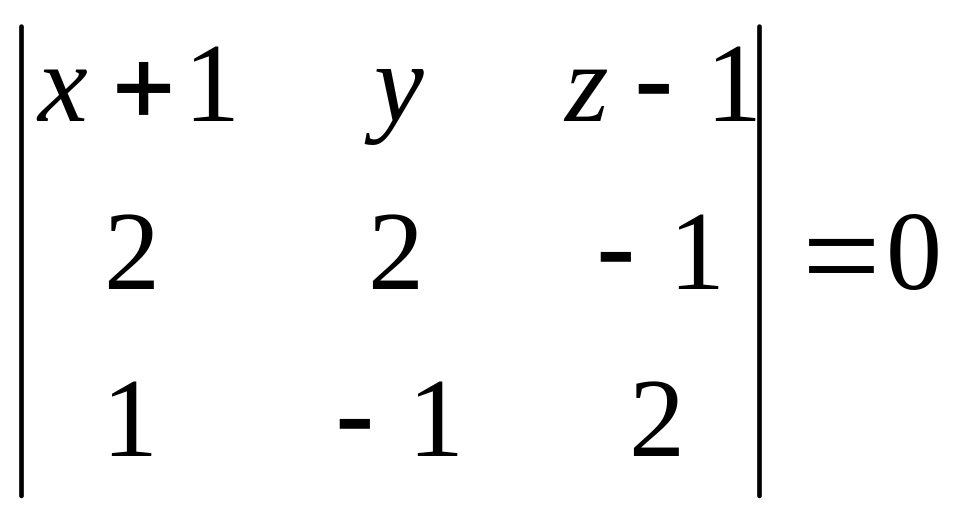т.е. или . 

Канонические и параметрические уравнения прямой в пространстве

Пусть в пространстве дана прямая. Ненулевой вектор , лежащий на прямой или параллельный ей, называется направляющим вектором этой прямой. Заметим, что если  направляющий вектор и число не равно 0, то вектор тоже направляющий. В частности при получается направляющий вектор единичной длины (орт вектора ).

Пусть  направляющий вектор данной прямой и точка лежит на этой прямой. Точка лежит на данной прямой тогда и только тогда, когда векторы и коллинеарны. Отсюда получаются канонические уравнения прямой:

. (1)

Равенства (1) означают, что соответствующие координаты векторов и пропорциональны. Обозначим через каждое из равных отношений в уравнениях (1). И выразим через . В результате получим параметрические уравнения прямой:

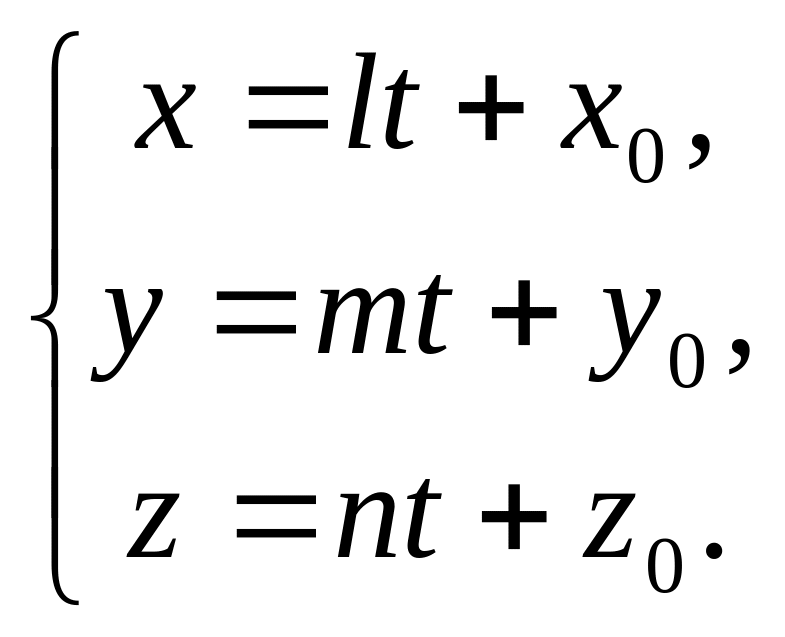(2)

Точка лежит на данной прямой тогда и только тогда, когда ее координаты могут быть получены из формул (2) при некотором значении параметра . В частности, при точка совпадает с . А при изменении параметра точка перемеща-ется по данной прямой.

Замечание. Формулы (2) раскрывают геометрический смысл уравнений (1) для случая, когда среди чисел есть нуль.