Выражение скалярного произведения через координаты векторов

Пусть ортонормированный базис пространства и пусть и - произвольные векторы пространства .

Утверждение. Справедлива формула

,

где и – координаты векторов и в базисе .

По условию,

и ,

где

, .

Пользуясь свойствами скалярного произведения, получаем

.

Следствие 1. Если

, ,

то

.

Следствие 2 . Если и ненулевые векторы, то косинус угла меду ними находится по формуле:

.

Следствие 3. Для того что бы векторы и были ортогональны, необходимо и достаточно, чтобы

.

Пример. Для точек найдем угол . Пусть . Тогда

,

и, следовательно,

, .

Ответ: . ð

Проекция вектора на направление другого вектора

Пусть и . Проекция вектора на направление вектора определяется равенством

,

где - угол вежду и . Аналогично,

.

Отсюда

= .

В частности,

, , .

Проекция вектора на произвольную ось  это, по определению, проекция вектора на направление орта оси . Обозначение: . Если – орт оси , то .

Проекция суммы двух векторов на одну и ту же ось равна сумме проекций:

,

так как . Аналогично для конечного числа векторов:

.

Кроме того, для любого числа проекция произведения равна .

Проекция нулевого вектора на направление произвольного ненулевого вектора и на произвольную ось считается равной нулю.

Векторное и смешанное произведения

Векторным произведением ненулевых векторов и называется вектор , определяемый тремя условиями:

1) , где – угол между и .

2) или .

3) Если , то - правая тройка (т.е. кратчайший поворот от к виден из конца вектора против часовой стрелки).

Если или , то векторное произведение и считают равным нулевому вектору.

Обозначения: или .

Из определения видно, что тогда и только тогда, когда векторы и коллинеарны.

В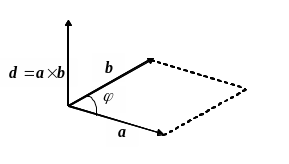 случае неколлинеарных векторов и модуль векторного произведения равен площади параллелограмма, построенного на векторах и : .

Если – орт вектора , то .

Справедливы свойства:

1 ,

2 (антикомутативность),

3 ,

4 .

Свойства 1 3 следуют непосредственно из определения векторного произведения, а свойство 4 докажем позднее.

Пусть  три произвольных вектора пространства . Если вектор векторно умножить на , а затем полученный вектор скалярно умножить на , то получится число , называемое смешанным произведением векторов .

Обозначение: .

Утверждение 1. Модуль смешанного произведения некомпланарных векторов равен объему параллелепипеда, построенного на векторах . При этом , если тройка правая, и , если тройка левая.

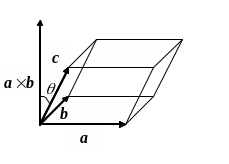Пусть - угол между векторами и . Объем параллелепипеда, построенного на векторах равен произведению его основания на высоту :

.

Если тройка правая, то и высота равна . В этом случае

.

Если тройка левая, то . В этом случае и .

Утверждение 2. Если смешанное произведение равно нулю, то сомножители компланарны.

Если не компланарны, то по предыдущему утверждению . Значит, если , то компланарны. Осталось доказать, что, если компланарны, то их смешанное произведение равно нулю. Если среди векторов есть нулевой, то равенство очевидно. Пусть все векторы отличны от нуля, но при этом компланарны. Если и коллиниарны, то и .

Если и не коллиниарны, то параллельны одной плоскости, но в этом случае

Утверждение 3. Для любых векторов верно равенство:

. (1)

Если векторы компланарны, то обе части равенства (1) равны нулю. Если векторы не компланарны, то модули обеих частей равенства (1) равны объему одного и того же параллелепипеда. По свойству коммутативности скалярного произведения . Кроме того, тройки и имеют одинаковую ориентацию, поэтому и знаки обеих частей равенства (1) одинаковы.

Замечание. Иногда, с помощью равенства (1) мотивируют обозначение (действительно, согласно (1) смешанное произведение не изменится, если в его определении поменять знаки векторного и скалярного произведений).

Смешанное произведение не меняется при перестановке векторов в круговом порядке.

Это следует из того, что при круговой перестановке векторов ориентация тройки не меняется.

При перестановке двух векторов смешанное произведение меняет знак:

, , .

Упражнение. Доказать, что если векторы линейно независимы, то векторы

, , .

тоже линейно независимы.

Пусть . Умножив обе части этого равенства скалярно на , получим:

,

где , . Аналогично , .