2. Методы изучения, анализа и прогнозирования спроса

Целью экономического развития является удовлетворение потребностей. Потребность в товарах народного потребления проявляется в форме спроса. Под спросом понимается часть общественной потребности, обеспеченной денежными средствами. Спрос характеризуется платежеспособной потребностью населения и определяется максимальной возможностью покупателей заплатить за товар. Величина (объем) спроса определяется наибольшим количеством товара, который покупатель готов купить по предложенной цене за некоторый период времени. Макроспрос — спрос на товары определенной товарной группы: на обувь, автомобили, меховые товары, мебель; микроспрос — спрос на конкретный товар: на лак мебельный, тетради ученические в клетку, на автомобиль Skoda Yeti. Закон спроса действует всегда, поэтому необходимо тщательно подходить к количественным методам изучения, анализа и прогнозирования спроса для обоснованного формирования объёмов заказов, поставок и продажи товаров, а пренебрежение или неумение во время решать эти задачи приводит к убыточному режиму работы предприятия вплоть да банкротства, что и наблюдается особенно часто в условиях кризиса.

Существуют различные методы изучения покупательского спроса в оптовой и розничной торговле. Для изучения и прогнозирования спроса создаются маркетинговые службы (отделы), которые изучают общий объем спроса (емкость рынка) и внутригрупповую структуру спроса на закупаемые товары. Оптовые закупки следует начинать с изучения спроса, потребностей на товары, покупательских намерений и других факторов, формирующих спрос, что и представлено на рис.1.1. Собранная информация о спросе позволяет обосновывать коммерческие решения по закупкам товаров.

Анализ данных изучения покупательского спроса позволяет обеспечить правильное соотношение между объемом производства и потребления, даст возможность активно воздействовать на промышленность в целях расширения и обновления ассортимента товаров и повышения их качества.

Изучение спроса населения можно проводить в двух направлениях: изучение общего объема спроса и группового ассортимента; изучение внутригруппового ассортимента, потребительских оценок качества и оформления товаров. Наиболее распространенной формой проявления спроса является показатель розничного товарооборота.Анализ структуры розничного товарооборота помогает выявить предпочтения покупателей в отношении тех или иных товаров. Розничные торговые предприятия применяют также определенные способы изучения спроса покупателей: анализ показателей товарооборота, товарных запасов и товарооборачиваемости; анализ реализованного и нереализованного спроса населения.

Анализ реализованного спроса заключается в изучении ассортиментной структуры товаров и учете движения товарных запасов, что позволяет определить, сколько и каких товаров продано.Величина реализованного спроса за некоторый период времени будет равна количеству проданного товара и может быть вычислена.

Методы изучения реализованного спроса можно разделить на методы непосредственной регистрации продажи товаров и методы, основанные на балансовых расчетах - наиболее распространенные, основанные на формуле товарного баланса:

где:З_н — остаток товаров на начало периода;

П — поступление товаров за период изучения спроса;

В_р —выручка за изучаемый период;

З_к — остаток товаров на конец периода.

В общем виде функция спроса представляет собой многофакторную модель связи уровня потребления материального блага D и факторов влияния, что можно записать в общем виде так:

D_а = f(p_а, p_в, p_с, p_д,p_е, p_л, u,W,T,F,S,G,Q_а,t),

где: p_а, p_в, p_с, p_д,p_е, p_л – цены товаров а,в,с,д,е,л;

u -ежемесячный доход покупателя,

W-уровень благосостояния покупателя,

T- сезон года потребности в товаре покупателя,

F- интенсивность рекламной деятельности;

S- соответствие моде,

Q_а-качество товара а,

G-пол, возраст и социальное положение покупателя,

t – временной интервал .

Шведский экономист Л. Торнквист предложил три вида однофакторных моделей связи объема спроса D от уровня u – дохода:

для предметов первой необходимости –

для менее необходимых предметов –

для предметов роскоши -

Для товаров длительного пользования (холодильники, телевизоры, мотоциклы, часы) применяют логистическую функцию вида:

Для товаров, потребление которых (овощи, сахар, фрукты) с ростом доходов семей увеличивается, а затем в последующем замедляется до уровня насыщения а_0, применяют гиперболическую форму связи:

В общем виде функция объёма предложения S_a товара а может быть представлена следующим выражением:

S_a = φ(p_а, p_в, p_с, p_д,p_е, p_л, N_а, Q_а, W_а,К_а,F_а,G_а, Т, П, t),

где: p_а, p_в, p_с, p_д,p_е, p_л –цены товаров а,в,с,д,е,л;

N_а-объём заказа клиентами на приобретение товара а,

Q_а-качество товара а,

W_а-размер предоплаты заказов клиентами на приобретение товара а,

К_а-конкурентоспособность предлагаемого товара а в товарной группе,

F_а-мнение покупателей о перспективе товара а,

Т- уровень развития изготовления товара а,

П- профессионализм исполнителей операций,

G_а -сезонность потребности в товаре а,

t – временной интервал.

Модели связи спроса D и предложения S c факторами влияния имеют разнообразные виды математических форм связи и соответственно графического отображения. Они являются основой для построения экономико-математической модели факторного анализа, параметры которой оцениваются методами математической статистики. Для создания трендовых моделей на основе кривых роста по прогнозированию развития экономических процессов методом экстраполяции распространены экспоненциальные кривые вида:

y=ab^t или y=c + ab^t

Параметры моделей определяются методом наименьших квадратов, затем проверка адекватности и точности модели и верификация прогнозов. Существуют специальные программы методов математической статистики для подбора математической формы связи в среде Excel на основе эмпирических данных, а заложенные методы корреляционно-регрессионного анализа позволяют определить математическую форму связи между результативным и факторными признаками, измерить тесноту связи между ними, оценить адекватность, качество модели и провести анализ влияния факторов. Так, например, проведенные исследования по изучению спроса, учитывающие объём поставки группы товаров на душу населения х₁(руб); среднедушевой уровень доходов населения региона u(руб); коффициент урбанизации х₃(%); индекс розничных цен х₄(%); средней розничной цене товара в группе p₅(руб) - позволили построить следующие многофакторные экономико-математические модели прогноза:

-для непродовольственных товаров

D_нп = ехр(- 2,665+ 1,361 lnu – 0,273t)

-для всех видов тканей

D_тк = ехр(3,264 + 0,278 lnu + 1,235 ln х₃ -0,477t)

-для трикотажа

D_тр = 35,076 + 0,095u – 174,45х₃ +0,29t

-для швейных изделий

D_шв = ехр(- 2,574 + 0,356 ln х₁ + 0,841u -0,137t)

-для обуви

D_об = - 5,942 + 1,351u – 0,945х₃ - 0,072t

- для шерстяных тканей

D_штк = ехр(8,424 -0,029lnu +4,34lnх₃ -0,508lnp₅ - 0,664t)

- для хлопчатобумажных тканей

D_хб = ехр(- 2,189 +0,537lnu - 1,34lnх₃ +0,147lnp₅ +0,213t)

Как правило зависимости спроса D от цены p имеют вид ниспадающих линий, чем меньше цена, тем больше спрос:

D = с - а p или D = с - а₀ехр(p) или D = с – а/p

В тоже время предложение растет с увеличением цены, поэтому зависимости S от p имеют вид нарастающих линий:

S = d + b p или S = d + b₀ ехр(b₁p ) или S = d + bpⁿ

Для экономики представляет интерес условие равновесия спроса и предложения:

D (p₀) = S(p₀),

При этом цена p_0, при которой выполняется это условие, называется равновесной.

Для анализа экономических процессов, например, функций спроса и предложения, которые являются фундаментальными категориями рыночной экономики, а также функций выручки, дохода, прибыли, издержек от различных факторов, используют понятие эластичности функции, которая показывает степень чуствительности к различным факторам. Эластичность Ех(у) определяется как предел отношения относительного приращения функции у к относительному приращению переменной х:

Е_x (у) = = = =

Эластично степенной функции у=хⁿ

Е_x (хⁿ) = = =

Эластичность экспоненты y = e^x

Е_x (е^x) = = =

Эластичность линейной функции у= ax + b

Е_x (ax+b) = =

Эластичность может быть использована при анализе функций спроса и предложения, которые являются фундаментальными категориями рыночной экономики, а также функцией выручки, дохода, прибыли, издержек от различных факторов.

Эластичность функции q=f(p) по цене р определяется формулой

Е_p(q) = =

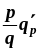
где q – количество покупаемого товара.

Эластичность спроса по цене показывает, на сколько процентов изменится спрос при изменении цены товара на 1%. Следует иметь в виду, что:если |Е(q)| > 1, то спрос эластичный, величина которого существенно зависит от цены товара; если |Е(q)| = 1, то спрос нейтрален; если |Е(q)| < 1, то спрос неэластичен, величина которого практически не зависит от цены, например, товары первой необходимости, такие как хлеб, мыло или соль.

Например, если функция спроса имеет вид:

q (p)=100-3p,

то эластичность спроса при цене р=20 у.е. равна

Ер(q)=20•(-3) (100-3•20) = -1,5

Следовательно при повышении (понижении) цены товара на 1% спрос на него понизиться ( повыситься ) на 1,5%.

Эластичность функции потребления S = f(p) по цене определяется выражением:

Ер (s)=

где: s- количество предполагаемого на продажу товара.

Допустим функции спроса и предложения имеют вид:

q = s =

Определим равновесную цену, эластичность спроса и предложения по цене и изменении дохода при изменении цены на ± 5 %

Равновесная цена определяется из условия равенства спроса и предложения:

= p² p_p = 1 у.е

Эластичность спроса

Ep_p (q) = = = -2

Эластичность предложения

Ep_p (s) = = = 2

Поскольку полученные значения эластичности по абсолютной величине больше единицы, то спрос и предложение являются эластичными по отношению к цене. Увеличение цены на 1% приведет к уменьшению спроса на 2%. При увеличении цена на 5% спрос уменьшается на 5•2=10%.

Отношение потребителя к возможным наборам товаров называется выбором потребителя. Если каждому набору товаров (х,у) поставить в соответствие потребительскую оценку в виде некоторого числа U, то получим функцию полезности потребителя U (х,у). Задачей потребительского выбора называется определение такого потребительского набора (х,у) который максимизирует егно функцию полезности при бюджетном ограничении, связанным с ценами р1 и р2 на товары соотношением р1х + р2х≤I.

Математическую формулировку задачи потребительского выбора можно записать в виде:

U(x,y) max

Решение задачи потребительского выбора при заданных ценах ограниченном бюджете I и функции полезности U( x,у) сведется к решению следующей системы уравнений:

Решение х* и у* системы уравнений является решением задачи потребительского выбора двух продуктов. Так, например если известна функция полезности U (xy)= , то дифференцируем заданную функцию и находим частные производные:

;

Затем подставляем в систему уравнений:

Функции спроса на первый и второй товар имеют вид:

;

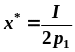если ,то ед. ед.

Расход на каждый товар составляет половину бюджета, а количество купленного товара равно затраченной сумме, поделенной на цену товара. Таким образом, расход на каждый товар составляет половину бюджета, а количество купленного товара равно затраченной сумме, поделенной на цену товара.

При формировании ассортимента товаров процесс анализа спроса всегда связан с решением задачи сравнения, выбора товара из предлагаемого множества. Выявить предпочтение на множестве товаров значит указать множество всех пар, для которых, например, товар а_i предпочтительнее а_j. В таком случае отношение предпочтения, доминирования при сравнении записывают как b_ij = 2, тогда b_ji = 0, а отношение безразличия, равнозначимости записывают как b_ij = b_ji = 1. В таком случае лицо, выбирающее решение, может провести попарное сравнение всех объектов этого множества, указав для каждой пары (а, b) наличие или отсутствие предпочтения. Например, можно осуществить выбор среди напитков: фанта, пепси, компот, чай, кофе, или мест будущей работы. Предпочтение можно представить в виде матрицы доминирования – безразличия на основе субъективного или коллективного анализа. Первичная информация задается в виде таблицы множества сравниваемых объектов а, b, c, d, e, наименования показателей р₁, p₂, p₃, ..., p_i, ..., p_n и их значений по каждому объекту, например, для товара а: р₁(а), p₂(а), p₃(a), ..., p_i(a), ..., p_n(a). Если по каждому показателю p_i можно вычислить его вес М_i, определяющий его значимость, то взвешенную сумму этих показателей можно рассматривать как суммарную оценку объекта а, его качество:

Тогда можно ввести решающее правило: обьект а предпочтительнее b, еслиQ(a) > Q(b). По указанной системе решающих правил отношение, выражающее доминирование, определяется построением матрицы попарного сравнения показателей, элемент которой b_ij определяется так:

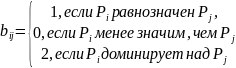
Рассмотрим решение задачи выбора легкового автомобиля табл. 1.1., где записано множество показателей, по которым можно провести их сравнение.

_{Т аблица 1.1.}

Показатель	Марка автомобиля
	Ford Focus	Hyundai Solaris	Mitsu- bishi Lancer	Toyota Corolla	Nissan Almera
Объем двигателя, см3	1587	1591	1590	1593	1596
Максимальная скорость, км/ч, Vmax	189	180	180	195	177
Время разгона до 100 км/ч, Tp, с	11,9	11	14	12,1	13,1
Расход топлива: город /шоссе/ средний, л/100 км, PT	10/5,8/ 7,5	8,6/5,2/ 6,5	9,4/6,1/ 7,3	8,4/5,7/ 6,7	8,7/5,5/ 6,6
Мощность, л. с., W	105	123	117	124	107
Масса снаряженная/ полная, кг, M	1290/ 1825	1110/ 1565	1255/ 1750	1300/ 1655	1185/ 1700
Рейтинг угоняемости, Py	4	5	2	1	3
Цена, тыс.руб.	620	560	679	659	540

Наиболее существенные показатели сопоставим с помощью метода парных сравнений, а результаты запишем в табл. 1.2.

_{Т аблица 1.2..}

	Ру	РТ	Тр	М	W	Vmax	Si	Mi	Ri
Ру	1	2	2	2	2	2	11	0,31	1
РТ	0	1	2	2	2	2	9	0,25	2
Тр	0	0	1	2	2	2	7	0,19	3
M	0	0	0	1	0	0	1	0,03	6
W	0	0	0	2	1	0	3	0,08	5
Vmax	0	0	0	2	2	1	5	0,14	4

После заполнения матрицы элементами сравнения находим по строкам суммы баллов (S_i) по каждому показателю:

где n – количество показателей, n = 6.

_{Правильность заполнения матрицы определяется равенством}

Затем определяем вес показателей M_i по формуле

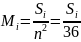_{Следует заметить, что}

Приоритет показателей распределяется по рангу R_i, который пропорционален значению коэффициента веса: чем больше его

значение, тем выше ранг, причем наибольшему значению M_i соответствует R_i = 1. На этом основании ранжированный перечень потребительских характеристик автомобиля будет иметь следую- щий вид:

^{1. Р}_у ^{– рейтинг угоняемости;}

^{2. Р}_Т ^{– расход топлива на 100 км, л;}

^{3. Т}_р ^{– время разгона до 100 км/ч, с;}

^{4. V}_max ^{– максимальная скорость, км/ч;}

5. W – мощность двигателя, л.с.;

6. М – масса, кг;

Для объективного вычисления значений целевой функции по каждому автомобилю введем балльную оценку этих показателей. Предположим, что чем лучше качественное содержание показателя, тем выше балл его оценки. Тогда, используя данные табл. 1.1., можно построить следующую матрицу балльных оценок Б_i(p_i) показателей табл. 1.3.

_{Т аблица 1.3.}

	1	2	3	4	5	Mi
Ру	1	2	3	4	5	0,31
РТ	7,2–7,4	6,9–7,1	6,6–6,8	6,3–6,5	6,0–6,2	0,25
Тр	13,1–14	12,1–13	11,1–12	10,1–11	9,1–10	0,19
Vmax	176–178	179–181	182–184	185–187	188–190	0,14
W	98–102	103–107	108–112	113–117	118–122	0,08
М	1570–1609	1610–1649	1650–1689	1690–1729	1730–1769	0,03

На основе данных табл. 1.3. можно вычислить значения интегральных оценок качества автомобилей без учета цены по формуле: n

^{На этом основании с учётом данных табл.1.3. можно записать:}

^Q(a_i ⁾ = 0,31^Б(Р_у ⁾+0,25 ^Б(Р_Т ⁾+0,19 ^Б(Т_Р⁾+0,14 ^Б(Vmax⁾⁺ +0,08^Б(W⁾+0,03^Б(М⁾

В соответствии с этим выражением вычислим интегральные оценки качества автомобилей:

Q_Focus = 0,31  4 + 0,25  5 + 0,19  3 + 0,14  5 + 0,08  2 + 0,03  5 = 3,82;

Q_Solaris = 0,31  5 + 0,25  4 + 0,19  4 + 0,14  2 + 0,08  5 + 0,03  4 = 4,11;

Q_Lancer= 0,31  2 + 0,25  1 + 0,19  1 + 0,14  2 + 0,08  4 + 0,03  5 = 1,81;

Q_Corolla= 0,31  1 + 0,25  1 + 0,19  3 + 0,14  3 + 0,08  5 + 0,03  1 = 1,98;

Q_Almera = 0,31  3 + 0,25  2 + 0,19  2 + 0,14  1 + 0,08  2 + 0,03  5 = 2,26.

^{Поскольку Q}_Solaris ^>Q_Focus^>Q_almera^>Q_Corolla ^>Q_Lancer, то следует выбрать автомобиль Hyundai Solaris. Если предположить, что интегральные оценки отображают качество автомобилей, то выбор можно провести по минимальному отношению цена/качество:

Ц/Q_Focus = 620/3,82= 162,3; Ц/Q_Solaris = 560/4,11=136,25;

Ц/Q_Lancer= 679/1,81=375,2;Ц/Q_Corolla=659/1,98=332,8; Ц/Q_Almera=540/2,26=238,9;

Минимальное отношение цена/качество показывает на выбор автомобиля Hyundai Solaris.

Можно добавить еще один критерий выбора - отношение цены к мощности двигателя (руб./л.с.): Focus – 5905, Solaris-4553, Lancer-5803, Corolla- 5315, Almera-5047, по которому выбор по минимальной стоимости одной л.с. приходится опять на Hyundai Solaris.

Можно воспользоваться и другой системой решающих правил. Считаем, что, например, автомобиль a₁ доминирует над a₂, если:

а) число показателей, по которым автомобиль a₁ лучше a₂, больше, чем число показателей, по которым автомобиль a₂ лучше автомобиля a₁;

б) для автомобиля a₁ ни один из показателей не принимает на- именьшего (наихудшего) значения.

При использовании этой системы решающих правил, учитывая бальную оценку и попарно сравнивая указанный перечень характеристик, получим следующую табл. 1.4.

_{Т аблица 1.4.}

Марка автомобиля	Марка автомобиля					Cумма баллов
	Focus	Solaris	Lancer	Corolla	Almera
Focus	–	0	1	1	1		3
Solaris	1	–	1	1	1		4
Lancer	0	0	–	0	0		0
Corolla	0	0	1	–	0		1
Almera	0	0	1	1	–		2

В соответствии с этими правилами выбор приходится тоже на автомобиль Hyundai Solaris.

После обсуждения решения задачи на площадке продаж автомобилей можно установить еще дополнительный перечень характеристик автомобиля: уровень цен на запчасти, стоимость страховки, обеспеченность рынка запасными частями, ремонтопригодность, затраты на доводку купленного автомобиля, наличие гаража, год начала выпуска модели автомобиля, стоимость нормочаса ремонта и техобслуживания, совокупные годовые затраты. На основе дополненных сведений можно провести глубокое и более аргументированное обоснование решения. По аналогии можно моделировать задачи формирования ассортимента товаров в товарных группах.

Материалы изучения покупательского спроса используются в коммерческой деятельности для решения двух взаимосвязанных задач: оптимального формирования товарного ассортимента торговых предприятий и своевременного пополнения ассортимента товаров на торговом предприятии путем их регулярного завоза в соответствии со спросом населения. Этому предшествует огромная работа на оптовых ярмарках, на фабриках производителей-поставщиков, с клиентами-покупателями и формированием заказов на поставку товаров. После завершения такой важнейшей работы по изучению, анализу и прогнозированию спроса, определению спроса D и предложения S и на этой основе формированием заявки Q в адрес поставщиков,после чего можно перейти к решению следующего класса задач - анализа, формирования и управления товарными запасами.

Контрольные вопросы:

1. Зачем следует изучать спрос и предложение?

2. Назовите факторы влияния на спрос и предложение?

3. Приведите примеры математических форм связи?

4. Какова последовательность изучения покупательского спроса?

5. Приведите примеры экономико- математических моделей спроса.

6. Каковы этапы построения моделей спроса и предложения?

7. Каково определение и назначение эластичности?

8. Как определить равновесную цену?

9. Каково решение задачи потребительского выбора?

10. Как решать задачи выбора товара из ассортимента?