
- •Курс лекций по дисциплине
- •230103 «Автоматизированные системы обработки информации и управления» (по отраслям)
- •230106 «Техническое обслуживание средств вычислительной техники и компьютерных сетей»
- •Часть III
- •Аннотация
- •Содержание
- •Введение
- •Глава 3.7. Обыкновенные дифференциальные уравнения
- •Лекция 38. Дифференциальные уравнения: основные понятия
- •Понятие дифференциального уравнения
- •Простейшие дифференциальные уравнения первого порядка
- •Дифференциальные уравнения с разделенными и разделяющимися переменными.
- •Приложение дифференциальных уравнений.
- •Лекция 39. Однородные дифференциальные уравнения первого порядка
- •Понятие однородного дифференциального уравнения первого порядка
- •Методика решения однородных дифференциальных уравнений первого порядка
- •Лекция 40. Линейные дифференциальные уравнения первого порядка
- •Понятие линейного дифференциального уравнения первого порядка
- •Методика решения линейных дифференциальных уравнений первого порядка.
- •Лекция 41. Дифференциальные уравнения второго порядка
- •Простейшие дифференциального уравнения второго порядка
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •Раздел 4. Основы теории комплексных чисел
- •Лекция 42. Алгебраическая форма комплексного числа. Геометрическая интерпретация комплексных чисел
- •Понятие мнимой единицы.
- •Пример 42.1. Вычислить: .
- •Алгебраическая форма комплексного числа.
- •Действия над комплексными числами в алгебраической форме.
- •Пример 42.2. Для комплексных чисел и найти: а) ; б) ; в) .
- •Решение квадратных уравнений с отрицательным дискриминантом.
- •Пример 42.4. Решить уравнение: .
- •Геометрическая интерпретация комплексных чисел.
- •Лекция 43. Тригонометрическая и показательная формы комплексного числа.
- •Понятие модуля и аргумента комплексного числа.
- •Тригонометрическая форма комплексного числа.
- •П ример 43.1. Изобразите на комплексной плоскости числа: , , .
- •Пример 43.2. Для комплексных чисел , найдите: а) ; б) ; в) ; г) .
- •Лекция 44. Переход между различными формами комплексных чисел.
- •Переход от тригонометрической и показательной формы
- •Переход от алгебраической формы к тригонометрической и показательной.
- •Раздел 6. Численные методы
- •Лекция 45. Приближенные величины. Действия с приближенными числами
- •Приближенные значения величин. В большинстве случаев при измерениях, вычислениях, выполнении операций над действительными числами получаются не точные, а приближенные значения величин.
- •Абсолютная погрешность.
- •Пример 45.1. При измерении диаметра детали, точное значение которого равно 25,2 мм, было получено приближенное значение 25 мм. Оцените абсолютную погрешность проведенного измерения.
- •Относительная погрешность.
- •Пример 45.2. Найти относительную погрешность измерения диаметра детали в примере 45.1.
- •Пример 45.3. При измерении длины l и диаметра d кабеля были получены значения м, мм. Оцените границы относительной погрешности и . Какое измерение проведено точнее?
- •Запись приближенных чисел. Верные и значащие цифры.
- •Пример 45.4. Найдите верные и сомнительные цифры в записи числа .
- •Погрешности вычислений с приближенными данными.
- •Пример 45.6. Произвести действия с приближенными числами:
- •Лекция 46. Методы приближенного решения алгебраических и трансцендентных уравнений
- •Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения. Введем понятия алгебраического и трансцендентного уравнения.
- •П ример 46.1. Определить промежуток, которому принадлежат корни уравнения .
- •Метод хорд.
- •Метод касательных.
- •Лекция 47. Приближенные методы вычисления определенных интегралов
- •Ф ормулы прямоугольников
- •Пример 47.1. Вычислите определенный интеграл :
- •Формула трапеций
- •Формула парабол (Симпсона)
- •Лекция 48. Численное решение обыкновенных дифференциальных уравнений методом эйлера
- •Задача численного решения дифференциальных уравнений.
- •Метод Эйлера.
- •Список использованной литературы
- •Справочные материалы дифференциальные уравнения
- •Операции над комплексными числами
Методика решения однородных дифференциальных уравнений первого порядка
Однородное уравнение
можно преобразовать к уравнению с
разделяющимися переменными при помощи
подстановки
![]() ,
где
,
где
![]() -
новая неизвестная функция.
-
новая неизвестная функция.
Найдем dy
по правилу нахождения производной
произведения:
![]() или
или
![]() .
.
Сформулируем алгоритм решения однородных дифференциальных уравнений:
Выполнить подстановки: и . В получившемся дифференциальном уравнении раскрыть скобки и привести подобные слагаемые. Должно получиться уравнение с разделяющимися переменными.
Проинтегрировать обе части уравнения с разделяющимися переменными относительно переменных x и z. Найти общее решение дифференциального уравнения.
В общем решении вернуться к переменным x и у, подставив вместо z выражение:
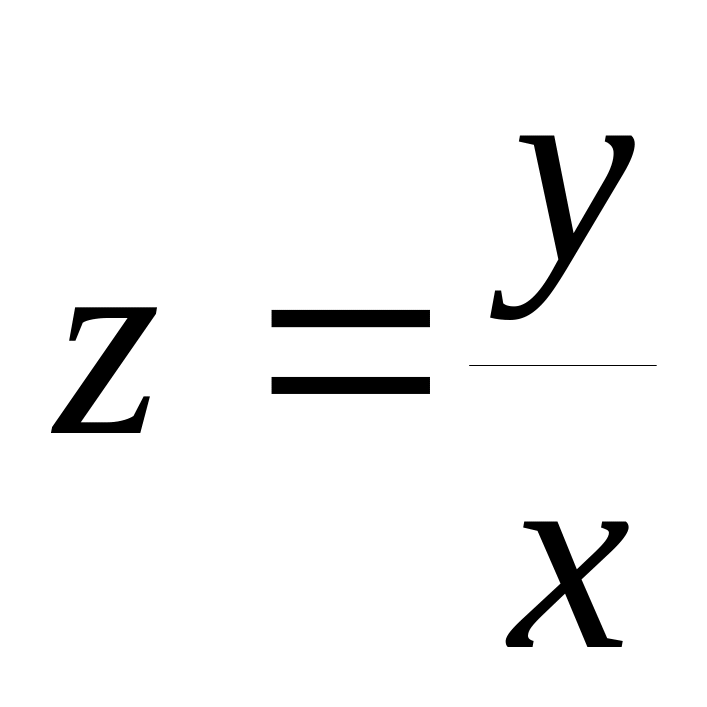 .
.Выписать в ответе получившееся общее решение дифференциального уравнения.
Пример 39.2. Найдите решение дифференциального уравнения: .
Решение. Данное уравнение – однородное дифференциальное уравнение первого порядка.
1. Выполним подстановки: и :
![]() .
.
Раскроем скобки:
![]() .
.
Приведем подобные слагаемые: первое и последнее взаимно уничтожаются. Получим:
![]() .
.
Перед нами уравнение с разделяющимися переменными. Соберем в левой части выражения, содержащие dx, в правой – выражения, содержащие dу.
![]() .
.
Тогда
![]() или
или
![]() - уравнение с разделёнными переменными.
- уравнение с разделёнными переменными.
2. Интегрируя обе
части, получим:
![]() или
или
![]() .
.
3. Подставим вместо
z выражение:
:
![]() или
или
![]() .
Это и есть общее решение исходного
однородного дифференциального уравнения.
.
Это и есть общее решение исходного
однородного дифференциального уравнения.
Ответ: .
Контрольные вопросы:
Какие функции называют однородными функциями п-го порядка?
Каков общий вид однородного дифференциального уравнения первого порядка?
Какие из приведенных ниже дифференциальных уравнений являются однородными: а)
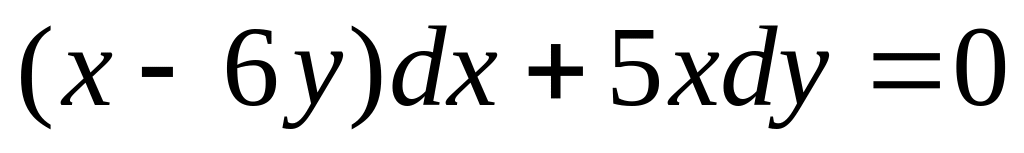 ;
б)
;
б)
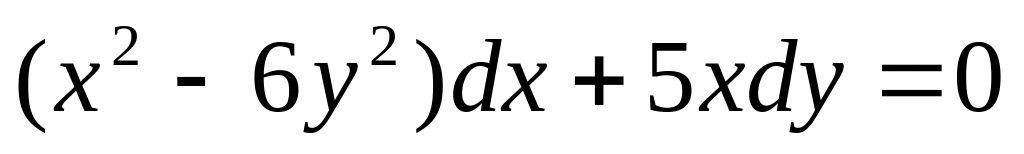 ;
в)
;
в)
 ;
г)
;
г)
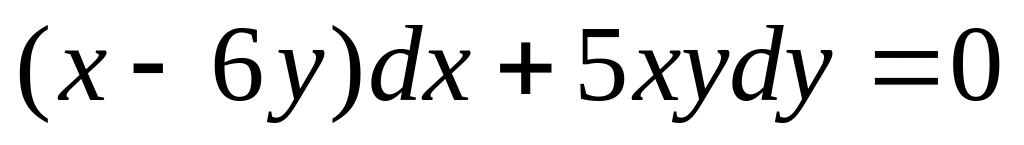 ;
д)
;
д)
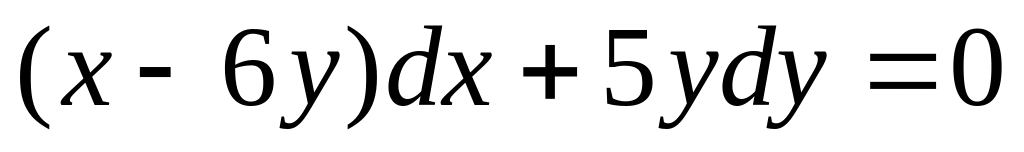 ;
е)
;
е)
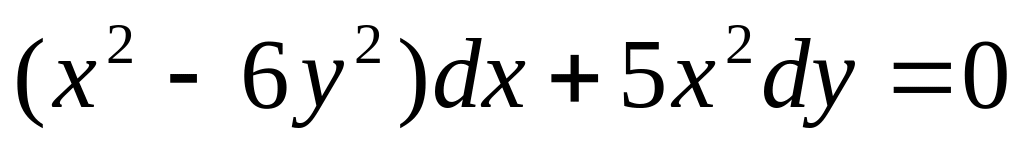 ?
?Какова методика решения однородных дифференциальных уравнений первого порядка?
Лекция 40. Линейные дифференциальные уравнения первого порядка
План:
Понятие линейного дифференциального уравнения первого порядка.
Методика решения линейных дифференциальных уравнений первого порядка.
Понятие линейного дифференциального уравнения первого порядка
Дифференциальное
уравнение первого порядка называется
линейным, если оно имеет вид
![]() ,
где
,
где
![]() и
и
![]() - заданные функции, содержащие только
переменную х.
- заданные функции, содержащие только
переменную х.
Данное дифференциальное уравнение получило название "линейное" поскольку содержит функции у и в первой степени (линейное относительно у и ).
Например, уравнение
![]() будет являться линейным, поскольку
имеет вид
,
где
будет являться линейным, поскольку
имеет вид
,
где
![]() ,
а
,
а
![]() .
.
Уравнение вида
![]() легко приводится к линейному делением
каждого слагаемого на х (множитель
перед
):
легко приводится к линейному делением
каждого слагаемого на х (множитель
перед
):
![]() или
или
![]() .
Полученное уравнение действительно
является линейным, поскольку имеет вид
,
где
.
Полученное уравнение действительно
является линейным, поскольку имеет вид
,
где
![]() ,
а
,
а
![]() .
.
Методика решения линейных дифференциальных уравнений первого порядка.
Чтобы решить
линейные дифференциальные уравнения
первого порядка применяют метод
Бернулли. Основа метода заключается
в том, что используется подстановка
![]() ,
где u и v
– некоторые функции от переменной х.
Тогда для нахождения
можно применить правило дифференцирования
произведения:
,
где u и v
– некоторые функции от переменной х.
Тогда для нахождения
можно применить правило дифференцирования
произведения:
![]() .
.
Рассмотрим сущность метода Бернулли на конкретном примере.
Пример 40.1. Найдите общее решение дифференциального уравнения .
Решение. Данное уравнение – линейное дифференциальное уравнение первого порядка.
Выполним подстановки: и :
![]() .
.
2. Сгруппируем члены, содержащие u, и вынесем u за скобки:
![]() ;
;
![]() (*).
(*).
3. Считая, что неизвестная функция у является произведением двух также неизвестных функций u и v, мы можем одну из этих функций (v) выбрать произвольно. Поэтому приравняем к нулю выражение, стоящее в скобках, и найдем функцию v:
![]() - уравнение с
разделяющимися переменными, для решения
которого представим
- уравнение с
разделяющимися переменными, для решения
которого представим
![]() .
Тогда:
.
Тогда:
![]()
![]()
![]() .
Взяв интегралы от обеих частей, получим,
что
.
Взяв интегралы от обеих частей, получим,
что
![]()
![]() .
Но поскольку функцию v
мы выбираем произвольно, удобно константу
С взять равной нулю. Тогда
.
Но поскольку функцию v
мы выбираем произвольно, удобно константу
С взять равной нулю. Тогда
![]() ,
а
,
а
![]() .
.
Таким образом, на третьем шаге мы нашли функцию v ( ).
4. Вернёмся к
уравнению (*). Поскольку выражение в
скобках на третьем шаге мы выбирали
равным нулю, то данное уравнение (*)
примет вид:
![]() или
или
![]() .
.
Подставим функцию в это уравнение и найдем вторую функцию и:
![]() .
Данное уравнение легко приводится к
простейшему делением обеих частей на
х:
.
Данное уравнение легко приводится к
простейшему делением обеих частей на
х:
![]() или
или
![]() .
Тогда
.
Тогда
![]()
![]() .
Константу С здесь писать обязательно!
.
Константу С здесь писать обязательно!
Итак, на четвертом шаге метода Бернулли мы нашли функцию и ( ).
5. Решением исходного
уравнения будет являться функция
.
Функции u и v
были найдены нами на 3-м и 4-м этапе решения
примера. Подставив их в уравнение
,
найдем, что
![]() - общее решение дифференциального
уравнения
.
- общее решение дифференциального
уравнения
.
Ответ: .
Из приведенного примера несложно установить алгоритм решения линейных дифференциальных уравнений первого порядка:
Привести дифференциальное уравнение к виду и ввести подстановки: и .
Сгруппировать члены, содержащие u, и вынести u за скобки.
Приравнять к нулю выражение, стоящее в скобках, и найти функцию v (необходимо решить дифференциальное уравнение с разделяющимися переменными v и х). Функция v не должна содержать константу С!
Вернуться к дифференциальному уравнению, полученному после шага 2. Подставить в это уравнение функцию v, найти вторую функцию и (функция и содержит константу С).
Подставить функции u и v, найденные на 3-м и 4-м этапе, в уравнение . Полученная функция у является общим решением исходного линейного дифференциального уравнения.
Замечание. На 3-м шаге решения линейного дифференциального уравнения требуется выразить функцию v через х. Во избежание возможных трудностей, рассмотрим некоторые конкретные примеры, показывающие, как из полученного уравнения выразить v:
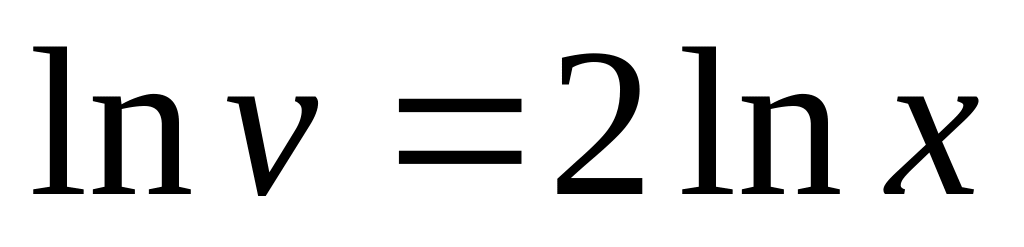

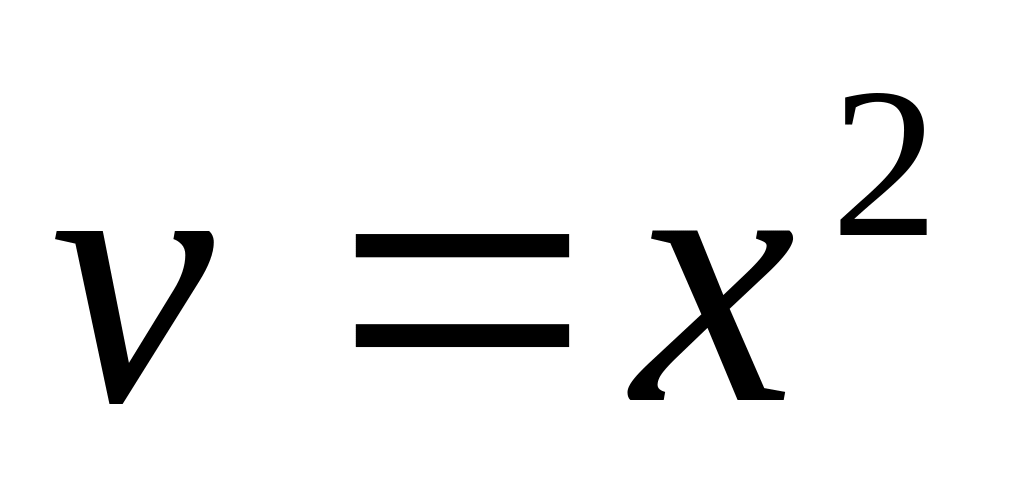 .
.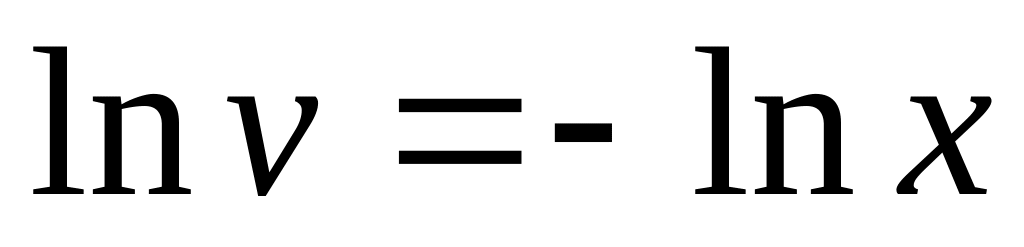
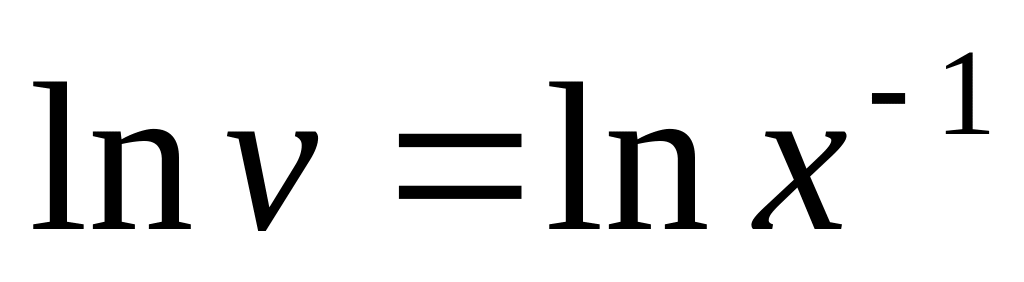
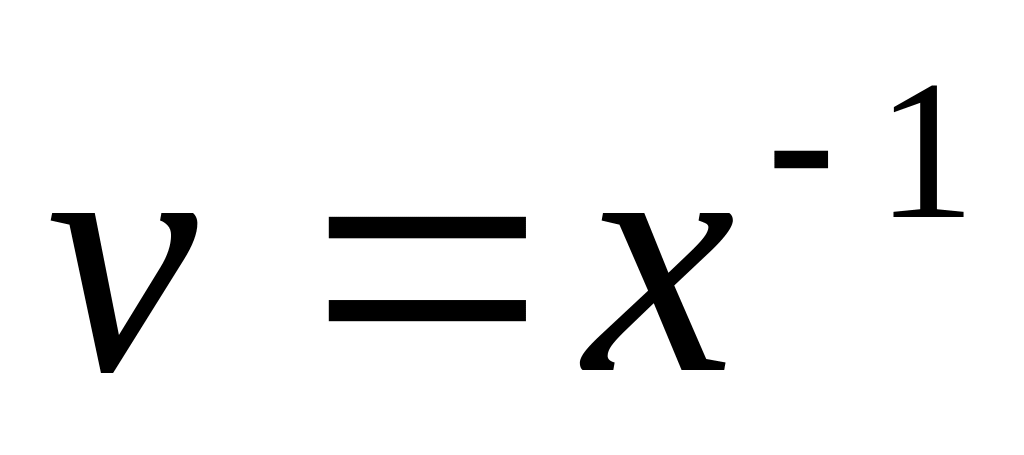
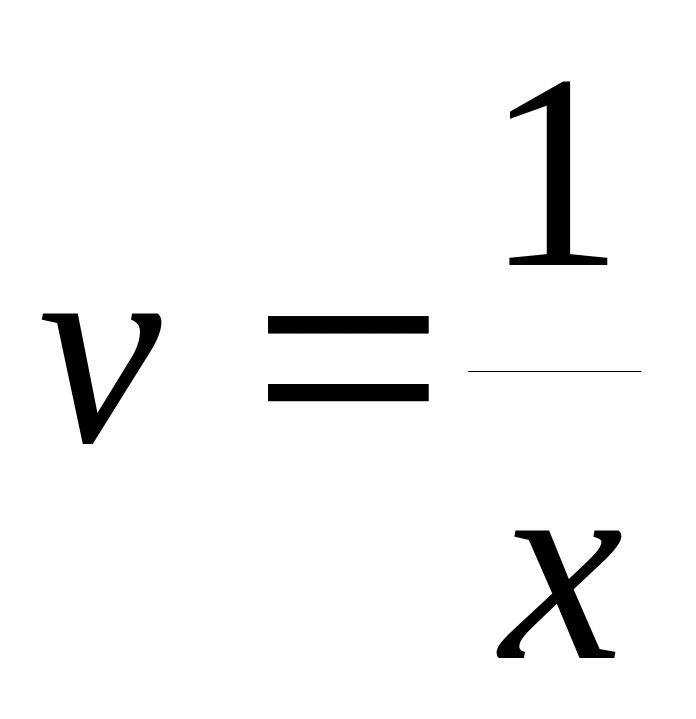 .
.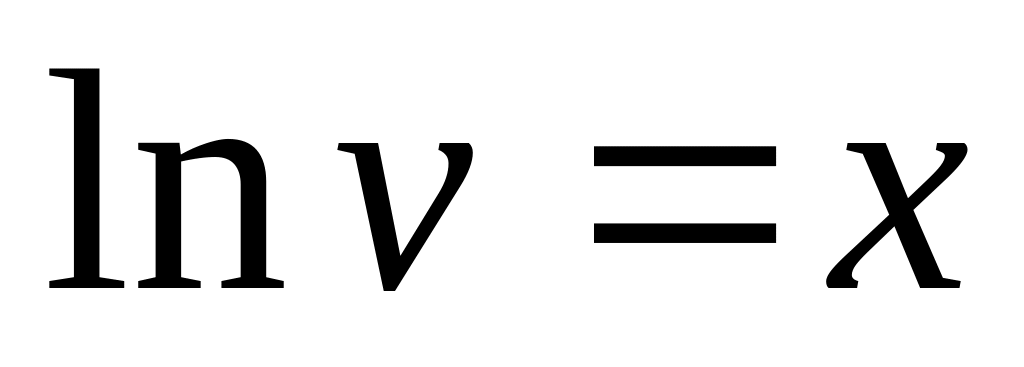
 .
.
Контрольные вопросы:
Каков общий вид линейного дифференциального уравнения первого порядка?
Какие из приведенных ниже дифференциальных уравнений являются линейными: а)
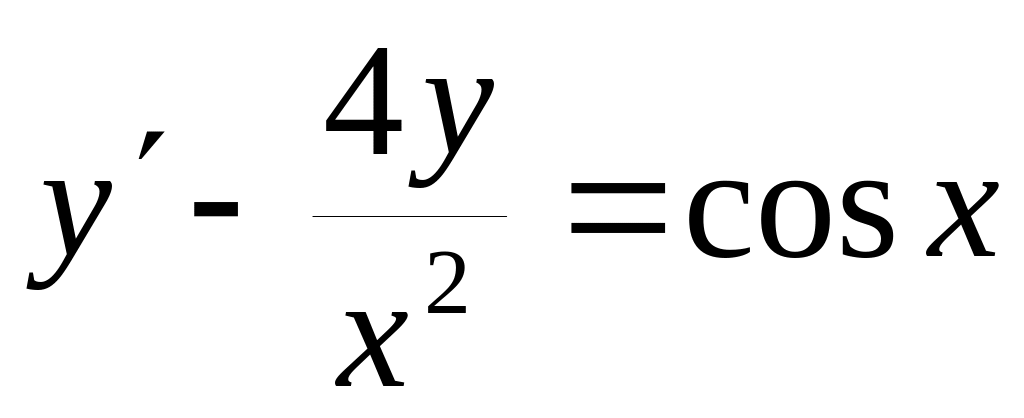 ;
б)
;
б)
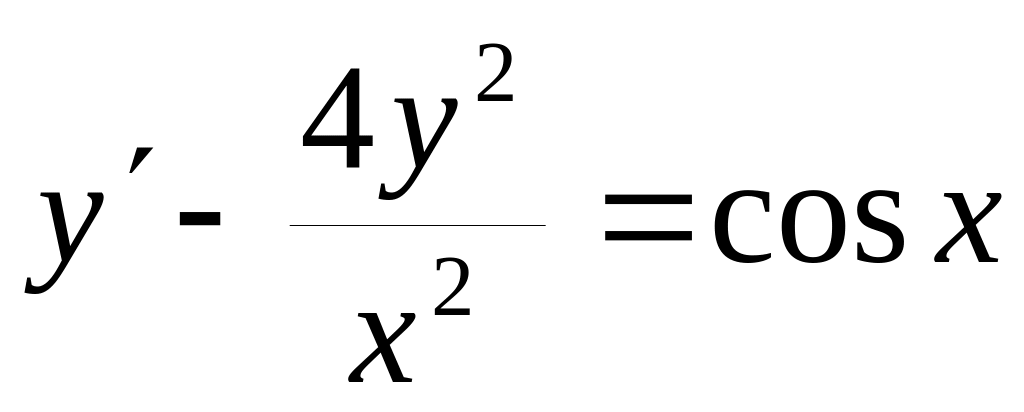 ;
в)
;
в)
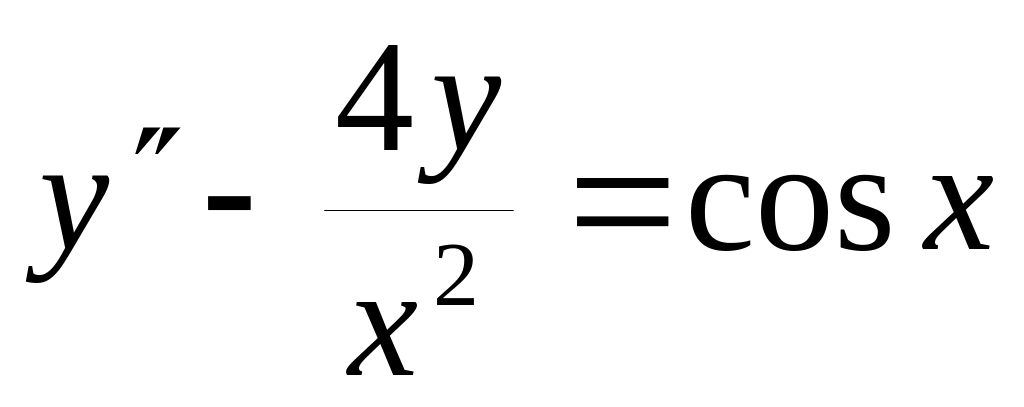 ?
?
Какова методика решения линейных дифференциальных уравнений первого порядка?
