2. Простейшие дифференциальные уравнения первого порядка

Рассмотрим дифференциальные уравнения первого порядка.

Уравнения вида назовём простейшими диф. уравнениями первого порядка.

Например, уравнения , - простейшие дифференциальные уравнения первого порядка. Обращаем внимание, что в левой части уравнения находится только , а в правой – выражение, содержащее только переменную х.

Для решения простейших дифференциальных уравнений первого порядка достаточно взять интеграл от правой и левой части по переменной х: .

Пример 38.2. Найдите решение дифференциального уравнения .

Решение. Поскольку перед нами простейшее дифференциальное уравнение первого порядка, найдем его решение по формуле :

;

у = - общее решение дифференциального уравнения .

Ответ: у = .

Пример 38.3. Найдите решение задачи Коши: , если .

Решение. Общее решение заданного дифференциального уравнения имеет вид: у= = (см. пример 38.2) . Воспользуемся начальными условиями: , следовательно, при . Подставим эти числа в общее решение:

. Выразим из данного уравнения С: .

Подставив найденное значение С в общее решение у = , получим следующее частное решение дифференциального уравнения: у = .

Ответ: у = .

3. Дифференциальные уравнения с разделенными и разделяющимися переменными.

Наиболее простым дифференциальным уравнением первого порядка является уравнение вида: . В нем в левой части стоит функция f(x), зависящая только от переменной х, а в правой – функция g(y), зависящая только от переменной у. Такое дифференциальное уравнение называют уравнением с разделенными переменными.

Для нахождения решения такого уравнения достаточно взять интеграл от обеих частей: .

Пример 38.4. Найдите решение дифференциального уравнения: .

Решение. Данное дифференциальное уравнение представляет собой уравнение с разделенными переменными. Проинтегрируем обе части уравнения:

. Тогда

- общее решение дифференциального уравнения .

Ответ: .

Если дифференциальное уравнение путем преобразований можно привести к виду , то оно называется дифференциальным уравнением с разделяющимися переменными.

Для решения такого уравнения необходимо:

1. Если в уравнении встречается , то представить его как .

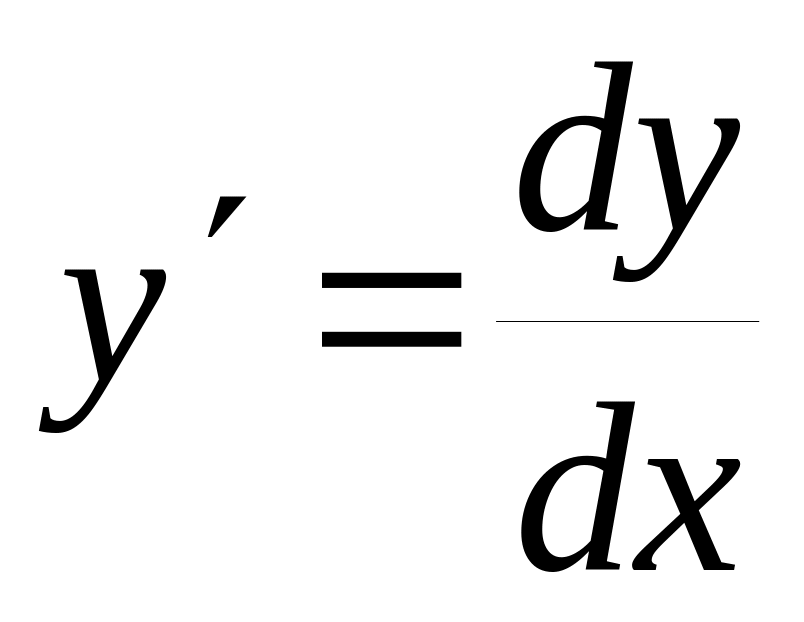2. Произвести разделение переменных (в одной части при dx собрать выражения, содержащие только переменную х; в другой части при dу собрать выражения, содержащие только переменную у).

3. Почленно проинтегрировать уравнение с разделенными переменными.

Пример 38.5. Найдите решение дифференциального уравнения: .

Решение. Данное уравнение – дифференциальное уравнение с разделяющимися переменными. Представим , тогда или .

Будем собирать множители с у в левой части, с х – в правой: .

Интегрируя обе части, получим: или - общее решение.

Ответ: .

Замечание. Иногда при нахождении решения дифференциального уравнения, каждое слагаемое которого представляет собой натуральный логарифм, в качестве константы можно выбирать . Такую операцию можно было бы произвести в примере 38.5. Тогда общее решение дифференциального уравнения имело бы вид: . Применим свойства логарифма: или . Откуда можно заключить, что . Этот прием особенно эффективен при решении задачи Коши.