3. Метод касательных.

П еред нами стоит все та же задача: найти корень уравнения вида с точностью ε, если известно, что корень принадлежит промежутку [а; b]. Как и в предыдущем пункте введем функцию на отрезке [а; b] (рис. 46.4), график которой пересекает ось Ох в некоторой точке С(с; 0). Цель метода не изменилась – найти абсциссу точки С – значение с.

Выполним следующие действия:

1. Проведем касательную к графику функции в точке В. Она пересекает ось Ох в точке с абсциссой х₁.

2. Выберем точку на кривой, абсцисса которой равна х₁ – точка В₁.

3. Проведем касательную к графику функции в точке В₁. Она пересекает ось Ох в точке с абсциссой х₂.

4. Выберем точку на кривой, абсцисса которой равна х₂ – точка В₂ и т.д. до тех пор, пока не будет справедливо неравенство: .

Выведем формулы для нахождения х₁, х₂… х_п+1:

1. Выпишем координаты точки В: .

2. Составим уравнение касательной, проведенной к графику функции в точке В: .

3. Найдем точку пересечения касательной с осью Ох. Она имеет координаты (х₁; 0). Заменим в уравнении пункта 2 х на х₁, у на 0: .

Выразим х₁. .

4. Поскольку для нахождения х₂ нужно проводить новую касательную в точке 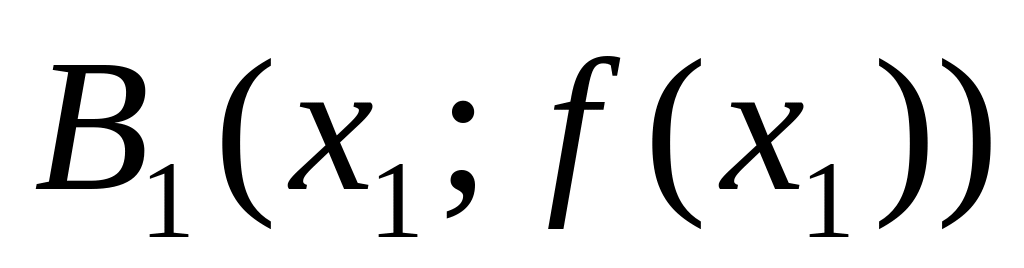и находить точку ее пересечения с осью Ох, произведем по аналогии следующую замену: роль b будет выполнять х₁, роль х₁ - х₂. Получим, что .

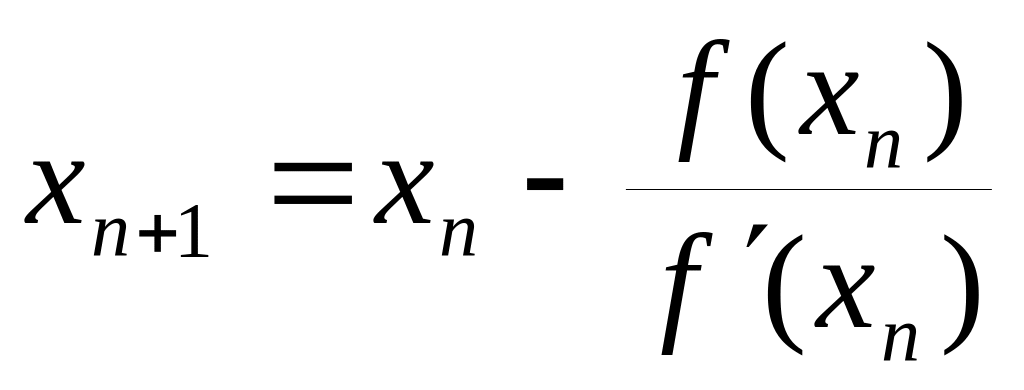5. О бобщим проведенные рассуждения. Для нахождения х_п+1 будем использовать следующую формулу: (4).

В рассмотренном нами случае исходной точкой, в которой проводилась первая касательная, была точка В.

Возможен и другой вариант: исходной может быть точка А (рис. 46.5).

Правило выбора исходной точки:

Исходной точкой является тот конец отрезка [а; b], для которого знак функции совпадает со знаком второй производной в данной точке.

Пример 46.3. Найти приближенное решение уравнения на [0; 1], использую метод касательных с точностью ε = 0,01.

Решение. Составим функцию .

1. Выберем исходную точку. Воспользуемся решением примера 46.2, где было показано, что для знак функции совпадает со знаком второй производной. Следовательно, точка В будет являться исходной, а - абсцисса исходной точки.

2. В силу достаточной сложности вычислений при применении данного метода, выполним расчеты в программе Microsoft Excel.

В качестве шапки таблицы возможен следующий вариант:

В столбце А будет указываться номер выполняемого шага п. Первое значение п выберем равным 0.

В столбце В будут располагаться значения х₀, х₁, х₂ и т.д. В качестве х₀ в ячейку В2 заносится координата х исходной точки. В нашем примере это .

В столбце С будут содержаться значения функции в точках х₀, х₁, х₂ и т.д., необходимые для расчета х_п+1 по формуле (4). Поскольку , то в ячейку С2 введем формулу: =B2^3+2*B2-1.

В столбце D будут содержаться значения производной функции в точках х₀, х₁, х₂ и т.д., необходимые для расчета по формуле (4). Поскольку , то в ячейку D2 введем формулу: =3*B2^2+2.

В столбце E будет осуществляться проверка того, не превосходит ли заданной точности ε. Эта проверка будет начинаться с первого шага, и ячейка Е2 не заполняется. После заполнения второй строки таблица будет иметь вид:

Начнем заполнение третьей строки. Номер шага в ячейке А3 будет равен 1.

Для расчета х₁ в ячейке В3 применим формулу (4), которая в программе Microsoft Excel примет вид: =B2-C2/D2.

Для расчета f(х₁) в ячейке С3 достаточно просто скопировать формулу из ячейки С2, и она будет иметь вид: =B3^3+2*B3-1.

Аналогично для расчета в ячейку D3 достаточно скопировать формулу из ячейки D2, и она будет иметь вид: =3*B3^2+2.

В ячейку Е3 занесем формулу для расчета модуля разности между последующим и предыдущим значением х: =ABS(B3-B2). Произведем проверку: если содержимое этой ячейки больше ε, то расчеты необходимо продолжить, меньше – закончить.

После заполнения третьей строки таблица будет иметь вид:

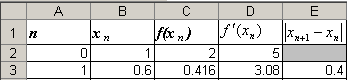
Как отмечалось выше, все формулы уже введены, в дальнейшем будем использовать только автозаполнение и осуществлять проверку в столбце Е. После выполнения следующих шагов таблица будет иметь вид:

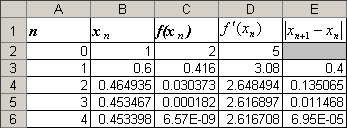
Видим, что в ячейке D6 содержимое 6,95Е-0,5 (означает ) стало меньше заданной точности ε = 0,01, следовательно, расчеты следует закончить и в качестве приближенного решения уравнения взять последнее х_п с точностью два знака после запятой. В нашем примере это х₄ 0, 45.

Ответ: х 0, 45.

Контрольные вопросы:

1. Какие уравнения называют алгебраическими? Трансцендентными?

2. Из скольких этапов состоят методы приближенного решения уравнений?

3. В чем заключается сущность метода хорд?

4. В чем заключается сущность метода касательных?