4. Техника вычисления пределов.
Рассмотрим правило нахождения предела функции в точке хо.
4.1. Если под знаком предела стоит многочлен, то предел вычисляется простой подстановкой (приём замены аргумента его предельным значением).
Пример 9.3.
Вычислите:
.
Решение. Подставим в многочлен вместо х значение -1, тогда
=
.
4.2. Если под знаком
предела стоит отношение двух многочленов
,
то проверяем, обращается ли при подстановке
хо знаменатель в ноль.
Если не обращается, то предел вычисляется
простой подстановкой (см. пример
9.2).
Если при подстановке хо знаменатель обращается в ноль, то необходимо использовать дополнительные приемы.
Если
,
то имеем неопределенность вида
.
В этом случае предел
можно вычислить разложением многочленов
и
на множители, используя формулы
сокращенного умножения и формулу
разложения квадратного трехчлена на
множители:
,
где х1 и х2 – корни
уравнения
.
Если разложение выполнено верно, то в числителе и знаменателе дроби должны получиться одинаковые множители, которые следует сократить. После сокращения предел вычисляется простой подстановкой.
Пример 9.4.
Вычислите
.
Решение.
Проверим, какие значения будут принимать
числитель и знаменатель при подстановке
вместо х значения 3:
,
.
Получили неопределенность вида
.
Разложим числитель
на множители по формуле разложения
квадратного трехчлена. Составим уравнение
и найдем его корни:
D
=
;
;
3
или
;
.
Тогда числитель
можно представить в виде произведения
двух множителей:
=
Знаменатель
разложим по формуле разности квадратов:
=
.
Вернемся к исходному пределу:
=
=
.
Ответ:
=
4.3. Если под знаком предела стоит дробь вида , включающая иррациональную функцию (функцию, содержащую корень), то домножаем числитель и знаменатель дроби на выражение, сопряженное иррациональному.
Пример 9.5.
Вычислите
.
Решение.
Поскольку при подстановке в числитель
и знаменатель вместо х значение 0,
получаем неопределенность
,
домножим числитель и знаменатель дроби
на выражение
,
сопряженное знаменателю. Получим:
=
.
В знаменателе дроби воспользуемся формулой разности квадратов:
.
Вынесем в знаменателе
х за скобки
и сократим дробь на х:
.
Видим, что при подстановке х=0 числитель и знаменатель не обращаются в 0, следовательно, теперь предел вычисляется простой подстановкой:
=
=
=-8.
Ответ: =-8.
5. Предел функции на бесконечности
Рассмотрим определение предела функции при →∞.
Число b
называется пределом функции
при
→∞,
если для любого наперед заданного
существует такое
,
что для всех
имеет
место неравенство:
.
Если b
есть предел функции
при
→∞,
то пишут:
.
П
оясним
смысл определения: какую бы точность ε
мы ни задали, найдется число М,
такое, что при выборе
,
значения функции будут отличаться от
b на число, меньшее ε
(т.е. значения функции практически не
будут отличаться от b).
В качестве примера
рассмотрим всем хорошо известную функцию
(рис. 9.7) и покажем, что ее предел при
→∞
равен 0.
Пусть ε=0,01.
Тогда можно подобрать число М=100, и
для всех
модуль разности
будет
меньше точности ε. Таким образом,
.
Это согласуется и с нашим наглядным
представлением: если выбирать достаточно
большие значения х, значения
переменной у практически не будут
отличаться от 0.
При нахождении
пределов функций будем пользоваться
двумя основными пределами:
и
,
где с – константа.
Для вычисления предела дроби при →∞ будем использовать следующее правило: разделим каждое слагаемое числителя и знаменателя на х в наивысшей степени. Возможны три случая:
5.1. наивысшая степень числителя совпадает с наивысшей степенью знаменателя:
Пример 9.6.
Вычислите
.
Разделим каждое слагаемое числителя и знаменателя на х2. Получим:
=
=
;
Каждое слагаемое
стремится к 0 при
→∞,
тогда
=
=2.
Итак, если наивысшая степень числителя совпадает с наивысшей степенью знаменателя, то в пределе получается число, отличное от нуля.
5.2. наивысшая степень числителя больше наивысшей степени знаменателя:
Пример 9.7.
Вычислите
.
Разделим каждое слагаемое числителя и знаменателя на х2. Получим:
=
=
=∞.
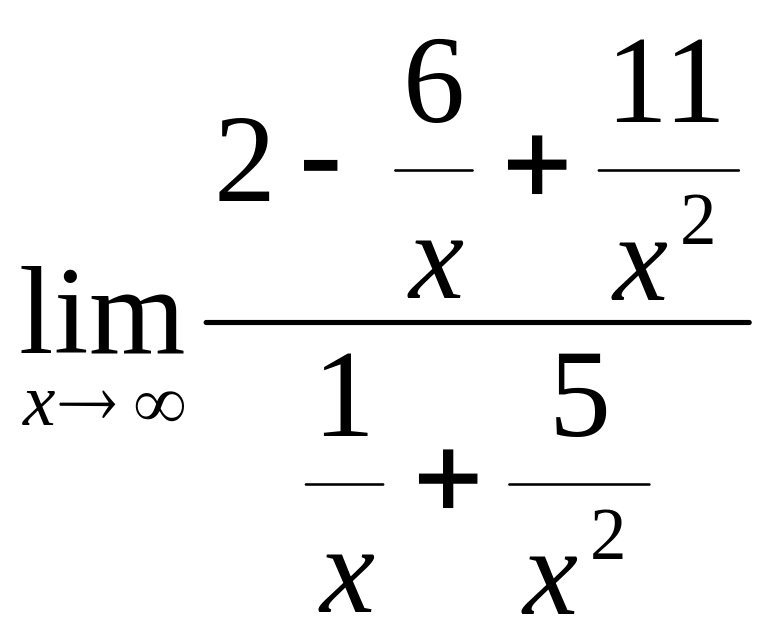Таким образом, если наивысшая степень числителя больше наивысшей степени знаменателя, то в пределе получается бесконечность.
5.3. наивысшая степень числителя меньше наивысшей степени знаменателя:
Пример 9.8.
Вычислите
.
Разделим каждое слагаемое числителя и знаменателя на х3. Получим:
=
=
=
.
Таким образом, если наивысшая степень числителя меньше наивысшей степени знаменателя, то в пределе получается ноль.