2). Вычитание векторов.

Под разностью векторов и понимается вектор = - , равный сумме вектора и вектора, противоположного вектору : = + (- ) (рис. 5.8.).

-

= -

Рис. 5.8.

Отметим, что в параллелограмме, построенном на векторах и , одна направленная диагональ является суммой векторов и , а другая – разностью (рис. 5.9.).

O

Рис. 5.9.

3). Умножение вектора на число.

П роизведением вектора на число  называется вектор (или ), который имеет длину , коллинеарен вектору , имеет направление вектора , если  > 0 и противоположное направление, если  < 0.

Н апример, если дан вектор , то векторы и будут иметь вид (рис. 5.10):

Рис. 5.10

Линейные операции над векторами обладает следующими свойствами:

1. - свойство коммутативности,

2. - свойство ассоциативности,

3. ,

4. 

5. 

6. 

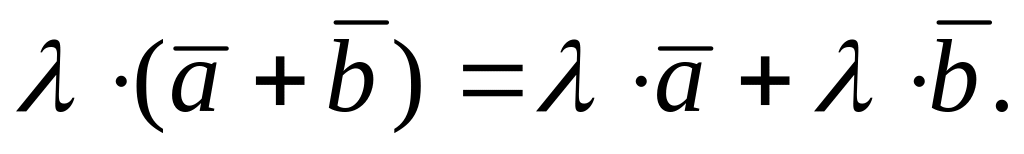
Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать выносить за скобки как скалярные, так и векторные общие множители.

3. Скалярное произведение векторов.

Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается . Итак, по определению, .

Свойства скалярного произведения:

1. .

2. .

3. .

4. .

4. Координаты вектора на плоскости и в пространстве.

Линейной комбинацией векторов называется сумма произведений этих векторов на какие-либо числа, например: .

Справедливы следующие теоремы:

1. Любой вектор плоскости может быть представлен единственным образом в виде линейной комбинации двух неколлинеарных векторов , т.е.

2. Любой вектор пространства может быть представлен единственным образом в виде линейной комбинации трёх некомпланарных векторов , т.е.

Говорят, что вектор разложен по базису.

Базисом на плоскости называется пара неколлинеарных векторов, взятых в определенном порядке. Базисом в пространстве называется три некомпланарных вектора, взятых в определенном порядке.

Введем понятие прямоугольной декартовой системы координат на плоскости и в пространстве. Прямоугольные координаты

на плоскости	в пространстве
Выберем в качестве базиса два единичных взаимно перпендикулярных вектора т.е. . Точку О примем за начало векторов и назовем началом координат.	Выберем в качестве базиса три единичных взаимно перпендикулярных вектора , т.е. Точку О примем за начало векторов и назовем началом координат.
Прямые, проведенные через векторы , называются осями координат, соответственно, осью абсцисс и осью ординат. Любой вектор плоскости можно единственным образом разложить по векторам : y 0 x Коэффициенты (x; y) разложения вектора по векторам называются координатами вектора.	Оси, определяемые единичными векторами, будем называть соответственно осью абсцисс, осью ординат и осью аппликат. Любой вектор пространства можно единственным образом разложить по векторам : z z y x Коэффициенты (x; y; z) разложения вектора по векторам называются координатами вектора.