
- •Что такое выборочный коэффициент корреляции. Формула
- •Как связаны теоретический и выборочный коэффициенты корреляции
- •Метод Монте-Карло
- •Эксперимент по методу Монте-Карло
- •Условия теоремы Гаусса-Маркова для модели парной регрессии
- •Опишите включение случайного члена в исходную модель, если преобразованная модель имеет вид
- •Опишите включение случайного члена в исходную модель, если преобразованная модель имеет вид
- •Метод Зарембки. Схема расчета
- •Тест Бокса-Кокса. Схема расчета
- •Опишите модель множественной регрессии
- •Постройте график зависимости общей величины расходов на питание от располагаемого личного дохода и цен на продукты питания.
Что такое закон распределения случайной величины
Совокупность значений {xk} случайной величины x с вероятностями {Pk}, с которыми она их принимает, называют законом распределения случайной величины.
Что такое дискретная и непрерывная случайные величины
Случайная величина дискретна, если результаты наблюдений представляют собой конечный или счетный набор возможных чисел. Случайная величина непрерывна, если ее значения лежат в некотором континууме возможных значений (на отрезке, интервале, луче и т.д.).
Что такое генеральная совокупность
Под генеральной совокупностью подразумеваются все возможные наблюдения интересующего показателя, все исходы случайного испытания или всю совокупность реализаций случайной величины х. Например, данные о доходах всех жителей какой-либо страны.
Что такое выборка
В большинстве случаев используется только часть возможных наблюдений, взятых из генеральной совокупности, и называется это множество (точнее подмножество) значений выборкой. Выборка – это множество наблюдений, составляющих лишь часть генеральной совокупности. Выборка объема n – это результат наблюдений случайной величины в вероятностном эксперименте, который повторяется n раз в одних и тех же условиях (которые могут контролироваться), и при неизменном распределении случайной величины х.
Что такое наблюдение
Наблюдение – наблюдаемое значение случайной величины или набора случайных величин.
Что такое математическое ожидание дискретной случайной величины
Математическое ожидание дискретной случайной величины – это взвешенное среднее всех ее возможных значений, причем в качестве весового коэффициента берется вероятность соответствующего исхода, т.е. сумма произведений всех возможных значений случайной величины на их вероятности.
Что такое математическое ожидание случайной величины
Математическое ожидание случайной величины часто называют ее средним по генеральной совокупности. Для случайной величины х это значение часто обозначается как µ.
Что такое теоретическая дисперсия
Важной
функцией переменной х является ее
теоретическая дисперсия, которая
характеризует меру разброса для
вероятного распределения. Она определяется
как математическое ожидание квадрата
разности между величиной х и ее средним,
т.е. величины (х-µ)2,
где µ - математическое ожидание х.
Дисперсия обычно обозначается как
 .
.
Из каких величин состоит случайная переменная

Часто вместо рассмотрения случайной величины как единого целого целесообразно разбить ее на постоянную и чисто случайную составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если х – случайная переменная и µ - ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом: x=µ+u, где u – число случайная составляющая (в регрессионном анализе она обычно представлена случайным членом).
Чему равно математическое ожидание случайной величины u. Почему
Математическое
ожидание величины u равно нулю.
Почему теоретическая дисперсия х равна теоретической дисперсии

Поскольку весь разброс значений x обусловлен u, то теоретическая дисперсия x равна теоретической дисперсии u, т.е.:


Что такое оценка, способ оценивания
Оценка, способ оценивания (estimator) – общее правило, формула для получения приближенного численного значения какого-либо параметра по данным выборки.
Что такое значение оценки
Значение оценки (estimation) – число, полученное в результате применения оценки к конкретной выборке; является случайной величиной, значение которой зависит от выборки.
Формула оценки теоретической дисперсии
Выборочное
значение
 обычно дает оценку для математического
ожидания, а формула
обычно дает оценку для математического
ожидания, а формула
 дает оценку дисперсии генеральной
совокупности.
дает оценку дисперсии генеральной
совокупности.
Что такое смещение
Смещение – разность между мат.ожиданием оценки и истинным значением оцениваемого параметра.
Что такое несмещенная оценка
Несмещенная оценка – оценка, имеющая нулевое смещение
Какой оценкой является
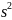 - смещенной или нет. Почему
- смещенной или нет. Почему
Величина
s2
является оценкой теоретической дисперсии
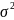 .
Математическое ожидание s2
равно
,
и эта величина является несмещенной
оценкой теоретической дисперсии, если
наблюдения в выборке не зависимы друг
от друга. Несмещенность этой оценки
обеспечивается коэффициентом
.
Математическое ожидание s2
равно
,
и эта величина является несмещенной
оценкой теоретической дисперсии, если
наблюдения в выборке не зависимы друг
от друга. Несмещенность этой оценки
обеспечивается коэффициентом
 .
.
Что такое эффективная оценка
Эффективная оценка – несмещенная оценка, имеющая наименьшую дисперсию среди всех несмещенных оценок.
Какую оценку выбрать несмещенную или эффективную
Существует вероятность, что одна оценка может быть несмещенной, другая иметь наименьшую возможную дисперсию. Выбор оценки исследователем зависит от обстоятельств, т.е. определяется функцией потерь, стоимостью сделанной ошибки как функцией ее размера, что осуществляется путем взвешивания функции потерь по функции плотности вероятности.
Как связаны дисперсия и размер выборки
Чем больше размер выборки, тем меньше дисперсия .
Что такое состоятельная оценка
Состоятельная оценка – оценка, у которой смещение и дисперсия стремятся к нулю при увеличении объема выборки.
Что такое выборочная ковариация и ковариация генеральной совокупности. Формула
Выборочная
ковариация является мерой взаимосвязи
между переменными.
При наличии n
наблюдений двух переменных (x
и y)
выборочная ковариация между x
и y
задается формулой:
 .
Для различения генеральной и выборочной
совокупности используется обозначения
.
Для различения генеральной и выборочной
совокупности используется обозначения
 для выборочной ковариации,
для выборочной ковариации,
 или
или
 для ковариации между x
и y
в генеральной совокупности.
для ковариации между x
и y
в генеральной совокупности.
Правила расчета ковариации
Если
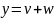 ,
то
,
то
 .
.Если
 ,
где а
-
константа, то
,
где а
-
константа, то
 .
.Если
 ,
где а
–
константа, то
,
где а
–
константа, то

Что такое выборочная дисперсия и дисперсия генеральной совокупности. Формула
Для
выборки их n
наблюдений
 выборочная дисперсия определяется как
среднеквадратичное отклонение в выборке:
выборочная дисперсия определяется как
среднеквадратичное отклонение в выборке:

Аналогичные
обозначения используются для дисперсии
 для выборочной дисперсии,
для выборочной дисперсии,
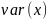 для генеральной совокупности.
для генеральной совокупности.
Правила расчета дисперсии (вариации)
Если , то
 .
.Если , где а - константа, то
 .
.Если , где а – константа, то

Если
 ,
где а
–
константа, то
,
где а
–
константа, то
 .
.
Что такое теоретический коэффициент корреляции. Формула
Подобно дисперсии и ковариации, коэффициент корреляции имеет две формы – теоретическую и выборочную. Теоретический коэффициент корреляции традиционно обозначается греческой буквой ρ. Для переменных х и у этот коэффициент определяется следующим образом:
 .
.
Если
х и у независимы, то ρ=0, так как равна
нулю теоретическая ковариация. Если
между переменными существую положительная
зависимость, то
 ,
а, следовательно, и
,
а, следовательно, и
 ,
будет положительными. Если существует
строгая положительная линейная
зависимость, то
,
будет положительными. Если существует
строгая положительная линейная
зависимость, то
 .
Если строгая отрицательная линейная
зависимость, то
.
Если строгая отрицательная линейная
зависимость, то
 .
.
Что такое выборочный коэффициент корреляции. Формула
Выборочный
коэффициент корреляции r
определяется путем замены теоретических
дисперсий и ковариации в выражении на
их несмещенные оценки, которые могут
быть получены путем умножения выборочных
дисперсий и ковариации на
 .
.
Следовательно,
 .
.
Множители
сокращаются, поэтому
 .
.
 при
строгой линейной положительной
зависимости между выборочными значениями
и у (когда на диаграмме рассеяния все
точки находятся точно на восходящей
примой линии).
при
строгой линейной положительной
зависимости между выборочными значениями
и у (когда на диаграмме рассеяния все
точки находятся точно на восходящей
примой линии).
 при
строгой линейной отрицательной
зависимости (точки лежат точно на
нисходящей прямой линии).
при
строгой линейной отрицательной
зависимости (точки лежат точно на
нисходящей прямой линии).
 показывает
отсутствие зависимости между наблюдениями
х и у в выборке.
показывает
отсутствие зависимости между наблюдениями
х и у в выборке.
При
не всегда
 ,
и наоборот.
,
и наоборот.
Как связаны теоретический и выборочный коэффициенты корреляции
Выборочная
корреляция
– несмещенная оценка теоретической
корреляции
 .
.
Метод Монте-Карло
Для решения вероятностных задач, в которых не удается установить формальную зависимость конечного результата от исходных данных, т.е. получить аналитическое решение задачи, используется метод Монте-Карло (метод статистических испытаний).
Основная идея метода состоит в следующем: вместо аналитического решения задачи либо проводят эксперименты, испытания, непосредственно рассматриваемые в задаче, либо эти испытания заменяют другими, имеющими с исходными одинаковую вероятностную структуру, или, иначе говоря, рассматриваемые в задаче случайные явления имитируют, моделируют другими случайными явлениями.
Одним из возможных способов имитации случайных явлений является рулетка. Определенные по результатам достаточно большого числа испытаний характеристики случайных явлений (относительные частоты, средние арифметические) используются в качестве приближенного решения задачи (в качестве оценок вероятностей, математических ожиданий). Допустимость этого приближения основывается на законе больших чисел.
Метод статистических испытаний применяют для решения не только тех задач, в которых в явном виде имеются случайные явления, но также и для решения многих математических задач, не содержащих таких явлений. В этом случае искусственно подбирается такое случайное явление, характеристики которого связаны с результатом решения исходной задачи. Для определения числовых значений этих характеристик используется метод статистических испытаний.
Так как достаточно высокая точность решения при использовании метода статистических испытаний гарантируется обычно при проведении большого числа испытаний, что возможно реализовать только на ЭВМ.
Эксперимент по методу Монте-Карло
Эксперимент по методу Монте-Карло – искусственный, контролируемый эксперимент, проводимый для проверки и сравнения эффективности различных статистических методов. Для определения насколько близкой к истине является та или иная оценка, в эксперименте по методу Монте-Карло исследователь задает все параметры модели, с помощью датчика случайных чисел моделирует «наблюдения» и к получившейся «выборке» применяет оценку. Эксперимент проводится много раз с разными значениями случайных чисел, после этого полученные результаты сравниваются с заданными, и делается вывод о качестве оценки.
Что такое зависимая переменная регрессии
Зависимая
переменная регрессии – переменная
величина в модели парной регрессии,
которую считают (по экономическим
соображениям) зависящей от другой
переменной. В модели
 зависимая переменная y.
зависимая переменная y.
Что такое объясняющая переменная регрессии
Объясняющая переменная регрессии (регрессор) – переменная величина в модели парной регрессии, от которой зависит (по экономическим соображениям) зависимая переменная. В модели объясняющая переменная х.
Что такое случайный член регрессии
Случайный член регрессии – слагаемое u в модели , которое описывает воздействие случайных факторов.
Причины появления случайного члена регрессии
Существует несколько причин наличия случайного члена u:
Невключение объясняющих переменных..
Агрегирование переменных.
Неправильное описание структуры модели.
Неправильная функциональная спецификация.
Ошибки измерения.
Что такое уравнение линейной регрессии. Описать
Уравнение
линейной регрессии – уравнение
 ,
где a
и b
– оценки параметров a
и b,
полученные в результате оценивания
модели регрессии
,
где a
и b
– оценки параметров a
и b,
полученные в результате оценивания
модели регрессии
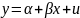 по данным выборки.
по данным выборки.
Что такое остаток в наблюдении. Формула расчета (см. п.5 алгоритмов расчетов)
Остаток
в наблюдении – разность
 между истинным значением переменной y
в i-том
наблюдении (
между истинным значением переменной y
в i-том
наблюдении ( )
и значением
)
и значением
 в i-том
наблюдении, полученным подстановкой
наблюдения
в уравнение линейной регрессии.
в i-том
наблюдении, полученным подстановкой
наблюдения
в уравнение линейной регрессии.
Вычисление
остатка в наблюдении по формуле:
 )
)
Метод наименьших квадратов. Формула расчета
Необходимо выбрать критерий подбора, который учитывал бы одновременно величину всех остатков. Наиболее разумным выбором является метод наименьших квадратов, который дает несмещенные и эффективные оценки α и β.
Метод наименьших квадратов (МНК) (OLS – Ordinary Least Squares) – метод нахождения оценок параметров регрессии, основанный на минимизации суммы квадратов остатков всех наблюдений.
Метод
наименьших квадратов (МНК) для модели
парной регрессии заключается в выборе
таких коэффициентов a
и b,
которые обеспечивают наименьшее значение
суммы:
 .
.
Формулы расчета коэффициентов а и b в модели парной регрессии (см. п.4 алгоритмов расчетов)
 ;
;

Что такое объясненная дисперсия зависимой переменной
Выборочная
дисперсия расчетных значений величины
y:

Что такое необъясненная дисперсия зависимой переменной
Выборочная
дисперсия остатков в наблюдениях:

Что такое выборочная дисперсия зависимой переменной регрессии
Выборочная дисперсия зависимой переменной регрессии равна сумме объясненной дисперсии зависимой переменной и необъясненной дисперсии зависимой переменной.
Что такое коэффициент детерминации. Формула
Коэффициент
детерминации – доля объясненной
дисперсии зависимой переменной во всей
выборочной дисперсии y.
Расчет коэффициента детерминации
 по формуле:
по формуле:

Что такое общая сумма квадратов отклонений. Формула
Сумма
квадратов отклонений величины y
от своего выборочного среднего
 .
.
 .
.
Что такое необъясненная сумма квадратов отклонений. Формула
Сумма
квадратов остатков всех наблюдений. или
или
 .
.
Что такое объясненная сумма квадратов отклонений. Формула
Сумма
квадратов отклонений величины
 от своего выборочного среднего
от своего выборочного среднего
 .
.
Теорема Гаусса-Маркова. Суть
На основе выборочных наблюдений производится оценка уравнения регрессии
 . Предполагается,
что x
- это неслучайная экзогенная переменная,
т.е. ее значения во всех наблюдениях
можно считать заранее заданными и никак
не связанными с исследуемой зависимостью.
. Предполагается,
что x
- это неслучайная экзогенная переменная,
т.е. ее значения во всех наблюдениях
можно считать заранее заданными и никак
не связанными с исследуемой зависимостью.
Величина
y
состоит из двух составляющих. Она
включает неслучайную составляющую ( ,
которая не имеет ничего общего с законами
вероятности (α
и
β
могут быть неизвестными, но, тем не менее
это постоянные величины), и случайную
составляющую u.
Отсюда следует, что когда мы вычисляем
b
по обычной формуле:
,
которая не имеет ничего общего с законами
вероятности (α
и
β
могут быть неизвестными, но, тем не менее
это постоянные величины), и случайную
составляющую u.
Отсюда следует, что когда мы вычисляем
b
по обычной формуле:
,
b
также содержит случайную составляющую.
 зависит от значений y,
а y
зависит от значений u.
Если случайная составляющая принимает
разные значения в n
наблюдениях, то мы получаем различные
значения y
и, следовательно, разные величины
и b.
зависит от значений y,
а y
зависит от значений u.
Если случайная составляющая принимает
разные значения в n
наблюдениях, то мы получаем различные
значения y
и, следовательно, разные величины
и b.
Теоретически существует возможность разложить b на случайную и неслучайную составляющие. Воспользовавшись соотношением , а также правилом 1 расчета ковариации, получим:

По
ковариационному правилу 3, ковариация
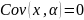 ,
по ковариационному правилу 2
,
по ковариационному правилу 2
 ,Причем
величина
,Причем
величина
 ,
следовательно:
,
следовательно:
 ,
т.о.
,
т.о.
 .
.
Таким образом, коэффициент регрессии b, полученный по любой выборке, представляется в виде суммы двух слагаемых:
Постоянной величины, равной истинному значению коэффициента β;
Случайной составляющей, зависящей от Cov(x,u), которой обусловлены отклонения коэффициента b от константы β.
Аналогично α имеет постоянную составляющую, равную истинному значению α, плюс случайную составляющую, которая зависит от случайного фактора u.
