31.4. Аналіз захищеності існуючих цп від атак на зв’язаних ключах

6Аналіз захищеності цп ecdsa та ec-kcdsa

У [108] наведені результати аналізу захищеності ЦП EC DSA та EC -GDSA від атаки на зв’язаних ключах. Відносно ЦП ECDSA показано, що якщо особисті ключі сеансу k1 і k2 є зв’язаними, наприклад , де n – порядок базової точки G, то і в різних повідомленнях Мі та Мj перші складові підпису r1 та r2 є однаковими. Далі, якщо особистий довгостроковий ключ виробити згідно з правилом

, (6.138)

де h₁ та h₂ є геш-значення для повідомлень Мі та Мj, то для повідомлень Мі та Мj будуть вироблені одинакові ЦП, тобто та .

Аналіз можливих наслідків відносно ЦП EC DSA дозволяє зробити такі висновки.

Загроза може бути реалізована тільки для двох наперед заданих Мі та Мj повідомлень.

Оскільки повідомлення Мі та Мj відомі та є відкритим ключем, то й інший порушник може виробити для свого повідомлення такий самий ЦП.

Із аналізу необхідно також зробити висновок, що при відомих та , тобто повідомленнях Мі та Мj, а також завжди доступних та n, порушник завжди може визначити особистий ключ. Таким чином, використання функції вирізання тільки х-координати при обчисленні відкритого параметра сеансу r ЦП робить стандарт EC DSA уразливим як щодо можливості створення колізій ЦП, так і визначення особистого ключа.

Якщо ці повідомлення обробляються в системі, то виникає загроза й для самого порушника, його особистий ключ d_a при виконанні «шахрайських» дій також компрометується. Для захисту від цієї загрози власник особистого ключа d_a повинен його змінювати відразу після появи двох таким чином підписаних повідомлень Мі та Мj.

Проведемо аналіз захищеності вдосконаленого алгоритму ЦП EC-KCDSA від атаки на зв’язаних ключах. Алгоритм ЦП EC-КСDSA визначено в [15, 16, 34]. Алгоритми вироблення та перевіряння ЦП EC-КСDSA наведено в табл. 6.17.

Таблиця 6.17

Алгоритми вироблення та перевіряння ЦП ЕС-КСDSA

Вироблення підпису	Перевіряння підпису
Вхід: особистий ключ da, загальні параметри, додаткове значення (геш-значення). Вихід: ЦП (r, s) для повідомлення М	Вхід: відкритий ключ , загальні параметри, додаткове значення (геш-значення), підписане повідомлення М΄, . Вихід: М΄ цілісне та справжнє чи ні
1. . 2. . 3. . 4. Перетворення на рядок байтів с. 5. Обчислення . 6. , якщо , то . 7.	1. Перевіряння, що та . 2. Обчислення геш-значення . 3. Обчислення , якщо , то . 4. Обчислення . 5. Перетворення на рядок байтів с. 6. Обчислення : якщо , то ЦП дійсний, інакше він відхиляється

Будемо вважати, що da є дійсним протягом деякого часу , а k1 і k2 є зв’язаними, причому . Тоді при виробленні підпису для Мі та Мj маємо:

Продовження таблиці 6.17

Для повідомлення Мі	Для повідомлення Мj
1. 2. 3. 4. 5. 6. 7.	1. 2. 3. 4. 5. 6. 7.

Розглянемо детально та порівняємо значення на кроці 3, що отримані з використанням ключів k1 і k2 відповідно. Визначимо умови, за яких -компоненти ЦП EC KCDSA співпадають, тобто для двох довільних різних повідомлень Мі та Мj. Використовуючи значення сьомих рядків, маємо:

(6.139)

або

(6.140)

Далі отримаємо, що:

або

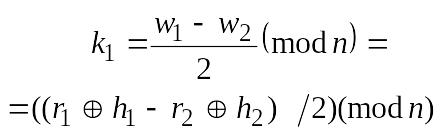(6.141)

Аналіз співвідношень (6.140) та (6.141) щодо захищеності EC-KCDSA дозволяє зробити такі висновки.

1. Значення відкритих ключів та відповідно для та не співпадають, тобто в алгоритмі EC-KCDSA при цих значеннях колізія компонент ЦП для двох довільних повідомлень Мі та Мj не відбувається. Це випливає з третього і п’ятого рядків, звідки видно, що

2. Співвідношення (6.141) вказує на умову здійснення атаки на зв’язаних ключах. Для здійснення атаки необхідно обчислити k6. Але k1 залежить від , яке у свою чергу односпрямовано, тобто через H(c1) залежить від k6. Складність розв’язання рівняння (6.141) має щонайменше субекспоненційний характер. Тому здійснення атаки на зв’язаних ключах для EC-KCDSA експоненційно складне і практично неможливе.

3. Таким чином, із алгоритмів стандарту ЦП ISO/IEC 15946-2 алгоритм ЦП EC-DSA є незахищеним від атаки на зв’язаних ключах, а алгоритм ЦП EC-KCDSA – захищеним.