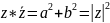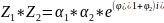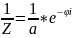Глава 5. Поле комплексных чисел с
Непустое множество К с бинарными операциями сложения и умножения называется полем(числовым полем), если выполнены следующие аксиомы:
Бинарные операции сложения и умножения являются замкнутыми.
Бинарные операции сложения и умножения являются коммутативными
A+b=b+a и a*b=b*a
Бинарные операции являются ассоциативными:
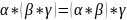
Имеет место закон дистрибутивности умножения относительно сложения.
Каждый ненулевой элемент имеет себе обратный, и каждый элемент имеет себе противоположный.
Общая группа аксиом связанных с другими свойствами элементов.
Рассмотрим поле действительных чисел R и на его основе рассмотрим множество всевозможных, упорядоченных пар вида (а,0) для которых выполняются законы:
Роль единичного элемента играет пара вида
,
а нулевого
Получается множество, состоящее из объектов отличных от действительных чисел, для которых выполнены все законы действительных чисел (включая законы 1-3 выше)
Таким образом поле действительных чисел R и новое множество являются изоморфными.
Теперь рассмотри
множество всех упорядоченных пар вида
Возникает вопрос, будет ли данное множество изоморфно множеству чисел R.
Такое множество найти МОЖНО!!!!!!(Он сам велел дофига знаков поставить)
Нужно лишь для пар определить законы:
Роль единичного элемента играет пара вида , а нулевого
Особую роль единичного элемента играет пара вида (0;1)
Перемножим
Элемент
изоморфен -1(числу).
То есть квадрат элемента (0;1) равен отрицательному числу..(!!!!!!)
Поэтому пара (0;1) обозначается I и называется «мнимой единицей» для которой имеет место
Множество всех упорядоченных пар образуют множество (с учетом законов 1-5), изоморфное множеству действительных чисел. Получившееся новое множество называется поле комплексных чисел С.
Алгебраическая форма комплексного числа
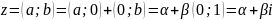
Модули комплексного числа z называется величина
Комплексное число
называется комплексно сопряженным
числу z
Теорема об отношениях сравнения на поле комплексных чисел С:
Поле комплексных чисел не является упорядоченным, то есть сравнивать 2 комплексных числа с помощью бинарного отношения типа сравнения (<,<=) невозможно.
Два комплексных числа называются равными, когда выполнено условие:
Простейшие свойства комплексных чисел:
Теорема об алгебраических операция над комплексными числами:
Пусть дано:
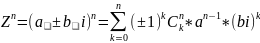(Короче обычное раскрытие скобок, по
биному ньютона)
Параграф 2. Комплексные числа в тригонометрической форме
Пусть дано число
(Тут какой то рисунок в лекции..я перерисовывать его не буду)
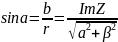
(Ребят, в ворде «альфа» не отличается почти от «а». не перепутайте! В аргументе у косинуса и синуса стоит «Альфа», а в самих формулах «а»)
Угол наклона комплексного числа к оси действительных частей называется аргументом комплексного числа.
(Тут опять же «альфа»)
Теорема (об операциях над комплексными числами в тригонометрической форме):
Пусть даны:
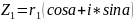
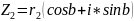
При делении комплексных чисел аргументы вычитаются, а при умножении складываются.
Возведение комплексного числа в степень (формула Муавра)
Общая формула Муавра
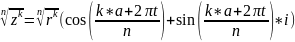
Комплексные числа в форме Эйлера.
Операции над комплексными числами в форме Эйлера:
Группа корней n-ой степени из единицы:
Комплексные числа
разбивают единичную окружность на
равные части. Получаем правильный
многоугольник.
При сложении и умножении чисел всегда получаются числа из этой же группы. Любое комплексное число можно выразить через