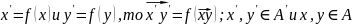Параграф3. Переход от базиса к базису. Координаты вектора относительно базисов.
Пусть даны две базисные системы
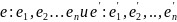
Согласно определению
ЛВП каждый вектор системы
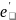можно представить в виде разложения по
векторам базиса системы е
Имеем:
……………………………………………
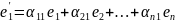
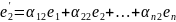
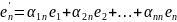
Запишем систему в матричной форме:
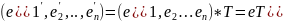
Где:
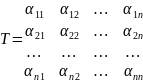
Матрица состоит из координат векторов системы записанных в виде разложения по векторам базиса системы e.
Матрица T
называется матрицей перехода от базиса
e (старый) базису
Вычленим, какие координаты будет иметь произвольный вектор x в новом базисе если он записан в старом.
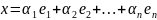
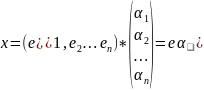
Так же вектор x может быть записан в новом базисе:
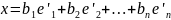
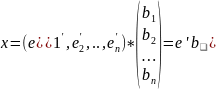
Хитрыми манипуляциями получаем
Пример: Матрица
перехода от
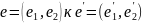с поворотом оси на a
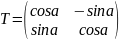
Параграф 4. Аффинные подпространства и r-мерные плоскости в аффинном пространстве.
Пусть дано ЛВП размерности n(dimV=n)
Рассмотрим произвольную систему линейных однородных уравнений от n переменных. Пусть ее ранг равен r.
Теорема (о подпространствах порожденных слоу): Совокупность всех решений СЛОУ образует линейное векторное подпространство размерностью n-r в ЛВП порожденного фундаментальной системой решений СЛОУ
Аффинные пространства:
В классическом определении ЛВП можно считать, что его элементами являются n-мерные точки. Расширим понятие ЛВП , добавив к его элементам понятие геометрического вектора, тем самым получим понятие точечно-векторного или аффинного пространства.
Пусть имеется ЛВП, элементами которого являются точки. Каждым любым двум точкам этого пространства однозначным образом сопоставим единственную упорядоченную пару этих точек, которую в дальнейшем будем называть геометрическим вектором(вектором).
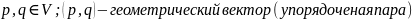
Точки и вектора в получившемся аффинном пространстве обладают следующими свойствами (аксиомы аффинного пространства):
Для каждой точки М и каждого вектора х существует точка N такая, что
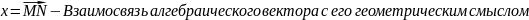
Для любых точек M,N и P выполнимо равенство :
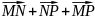
Совокупность всех точек ЛВП пополненная векторами, удовлетворяющих аксиомам, называют точечно- векторным или аффинным пространством. Аффинное пространство является n-мерным, если соответствующие ЛВП так же являются n- мерными.
Предложение(О простейших свойствах векторов аффинного пространства):
Если
.
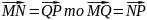Данное свойство непосредственно следует
из равенства
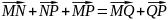
Вектор, у которого начало и конец совпадают, являются нулевым вектором n- мерного аффинного пространства.
Это следует
из равенства
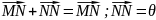
Для каждого вектора существует противоположный у нему вектор.
Это следует
из равенства:
Пусть задана т. О (начало координат) и система базисных векторов приложенных к точке О.
Согласно понятию ЛВП
вектор х есть
.
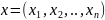То по аксиоме 1.АП (Аффинных пространств)
имеет место следующее OX=X
и
.
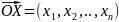Координатами вектора в АП считают
координаты соответствующего алгебраического
вектора
В случае когда заданы
произвольные 2 точки.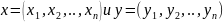
,
то
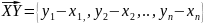
Действительно, рассмотрим равенство:
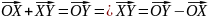
Что и требовалось доказать.
Теорема о изоморфизме аффинных пространств:
Естественным образом возникает вопрос, будут ли изоморфными 2 аффинных пространства в случае когда изоморфными являются соответствующие лвп.
Утвердительный ответ дается в Теореме (об изоморфизме аффинных пространств):
Любые два изоморфных аффинных пространства имеют одинаковую размерность (т.е они изоморфны только в этом случае)
Доказательство:
A и A’ называют изоморфными, если существует взаимно-однозначное отображение такое, что выполнены свойства:
Остальные свойства те же, что и свойства в определении изоморфизма ЛВП.
Выберем в каждом из А и А’ две точки такие, что координаты их будут равны, тогда имеет место следующее:
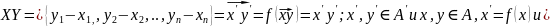
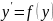
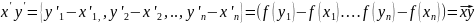
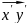является образом
при изоморфизме, что можно установить,
пользуясь понятием изоморфизма между
ЛВП и его простейшими свойствами.(все
тоже самое что и выше, только в обратном
порядке)
Переход от базиса к базису в аффинном пространстве:
Случай 1: Переход от базиса к базису имеющих общую точку приложения:
В данном случае переход осуществляется с помощью матрицы перехода, составленной из координат нового базиса. Преобразование координат вектора при таком переходе осуществляется с помощью известных алгебраических действий.
Случай 2: Переход от базиса к базису с изменением точки приложения базисных векторов.
Дальнейшие рассуждения
базируются на равенстве
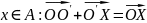
Координаты вектора при переходе от старого базиса к новому изменяются в соответствии с известными алгебраическими действиями с учетом вычитания вектора соединяющего точки приложения базисного векторов.
