2.1.3.2 Описание работы фильтра верхних частот в частотной области

Для расчёта частотной характеристики фильтра верхних частот (рисунок 2.4) воспользуемся формулой отношения напряжений, представленных в комплексной форме:

,

где — полное сопротивление фильтра верхних частот;

— коэффициент усиления;

— фазовый сдвиг. (2.5)

Определим частоту среза , как частоту, на которой амплитуда выходного сигнала ослабляется в раз (на 3 дб).

Из равенства , получим

,

где — круговая частота.

Фазовый сдвиг φ на этой частоте в соответствии с формулой (2.5) составляет 45º.

Амплитудно-частотная и фазово-частотная характеристики фильтра верхних частот приведены на рисунке 2.6. Из рисунка 2.6 видно, что амплитудно-частотную характеристику можно разбить на две асимптоты:

1 |A| = 1 = 0 дБ на высоких частотах ;

2 |A| ≈ ω·R·C на низких частотах ;

3 |A| = = -3 дБ на частоте .

2.1.3.3 Фильтр верхних частот как дифференцирующее звено

Из рисунка 2.1 видно, что падение напряжения на конденсатор C равно . Отсюда ток заряда конденсатора будет равен

На низких частотах выходное напряжение фильтра верхних частот намного меньше входного . В этом случая можно записать

.

Отсюда

.

То есть выходное напряжение пропорционально скорости изменения входного сигнала.

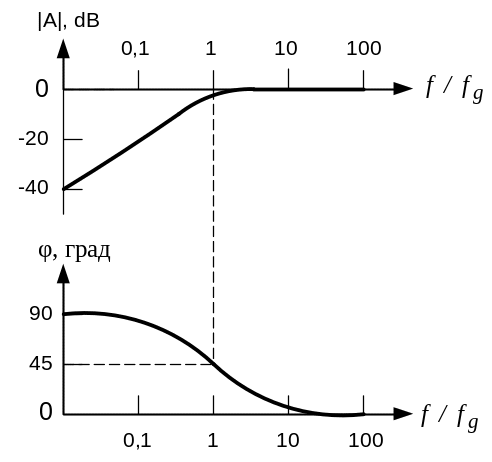
Рисунок 2.6 — Частотные характеристики фильтра верхних частот

2.1.3.4 Последовательное соединение нескольких фильтров верхних частот

При последовательном соединении нескольких фильтров верхних частот результирующую частоту среза можно определить по следующей формуле

.

Для случая n фильтров с равными частотами среза

.

2.1.4 Пассивный полосовой rc-фильтр

Полосовой фильтр получают путём последовательного соединения фильтров верхних и нижних частот. Выходное напряжение полосового фильтра имеет низкое значение на высоких и низких частотах и максимальное значение на резонансной частоте. Одна из возможных схем полосового фильтра представлена на рисунке 2.7.

Резонансная частота полосового фильтра, приведённого на рисунке 2.7 равна

.

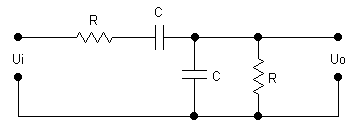
Рисунок 2.7 — Пассивный полосовой RC-фильтр

2.1.5 Резонансные схемы

Конденсаторы в сочетании с индуктивностями позволяют заострять частотную характеристику фильтра. На рисунке 2.8 приведена схема фильтра-пробки, которая содержит параллельный LC-контур.

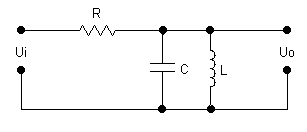
Рисунок 2.8 — Фильтр с параллельным LC-контуром

Сопротивление параллельного LC-контура на частоте равно

.

LC-контур в сочетании с резистором R образует делитель напряжения. На резонансной частоте и .

Резонансная частота соответственно равна

.

На рисунке 2.9 приведена схема фильтра с последовательным LC-контуром.

Рисунок 2.9 — Схема фильтра с последовательным LC-контуром

Сопротивление последовательного LC-контура на частоте равно

.

LC-контур в сочетании с резистором R образует делитель напряжения. На резонансной частоте и .

Резонансная частота соответственно будет равна

.

2.2 Порядок проведения экспериментов

2.2.1 Собрать схему (рисунок 2.10). В схему включены резистор 1 кОм, конденсатор 0,1 мкФ, генератор и осциллограф. В зависимости от требований отдельных пунктов лабораторной работы студент должен уметь самостоятельно изменять и дополнять схему подключения RC-цепи к измерительным приборам.

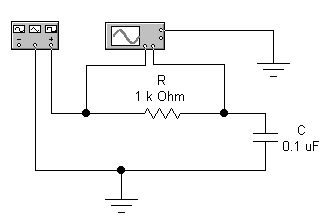
Рисунок 2.10 — Измерение постоянной времени RC-цепи

2.2.2 Измерение постоянной времени RC-цепи. Установит на генераторе следующие режимы работы: форма сигнала — прямоугольная; частота — 500 Гц, скважность — 2 (Duty cicle — 50%); амплитуда сигнала — 5 В, смещение (Offset) — 5В. Определить постоянную времени по времени спада выходного сигнала до уровня 37%, сравнить её с R·C. Определить максимальную частоту прямоугольных импульсов, которую может пропустить данная RC-цепь. Снять осциллограмму. Полученные результаты занести в таблицу 2.1.

Таблица 2.1 — Постоянная времени RC-цепи

Форма вх. Сигнала	Частота, Гц	R·C	tСПАДА до 37%	fMAX

2.2.3 Дифференцирующая цепь. Собрать схему (рисунок 2.11). Подать на вход RC-цепи прямоугольные импульсы положительной полярности частотой 100 кГц и скважностью 2. Объяснить форму выходного сигнала. Измерить постоянную времени RC-цепи и сравнить её с R∙C. Снять осциллограмму. Полученные результаты занести в таблицу 2.2.

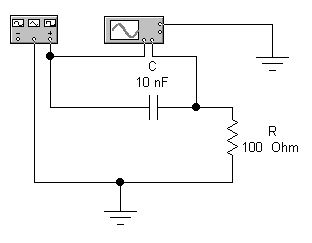
Рисунок 2.11 Дифференцирующая цепь

Таблица 2.2 Дифференцирующая цепь

Форма вх. Сигнала	Частота, Гц	Rf=0	Rf=∞	τ	R·C

2.2.4 Интегрирующая цепь. Собрать схему (рисунок 2.12). Подать на вход RC-цепи прямоугольные импульсы положительной полярности частотой 100 кГц, амплитудой 10 В и скважностью 2. Объяснить форму выходного сигнала. Измерить постоянную времени RC-цепи и сравнить её с R∙C. Снять осциллограмму. Полученные результаты занести в таблицу 2.3.

Таблица 2.3 Интегрирующая цепь

Форма вх. Сигнала	Частота, Гц	Rf=0	Rf=∞	Τ	R·C

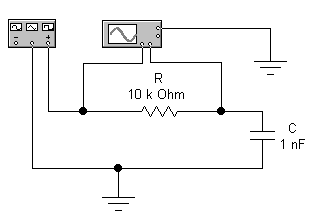
Рисунок 2.12 — Интегрирующая цепь

2.2.5 Фильтр нижних частот. Собрать схему (рисунок 2.13). Подать на вход RC-цепи синусоидальные колебания и снять амплитудно-частотную и фазочастотную характеристики фильтра (АЧХ и ФЧХ). Определить частоту среза.

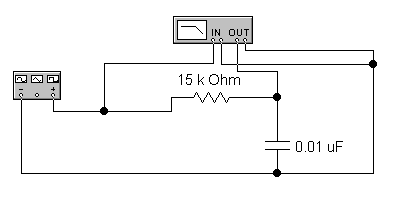
Рисунок 2.13 — Фильтр нижних частот

2.2.6 Фильтр верхних частот. Собрать схему (рисунок 2.14). Подать на вход RC-цепи синусоидальные колебания и снять амплитудно-частотную и фазочастотную характеристики фильтра (АЧХ и ФЧХ). Определить частоту среза.

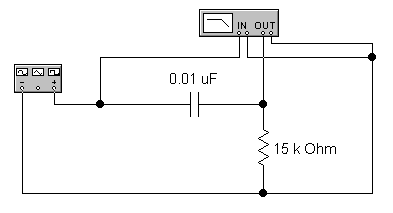
Рисунок 2.14 — Фильтр верхних частот

2.2.7 Резонансный контур. Собрать схему (рисунок 2.15). Подать на вход колебательного контура синусоидальные колебания и снять амплитудно-частотную и фазочастотную характеристики (АЧХ и ФЧХ). Определить резонансную частоту контура.

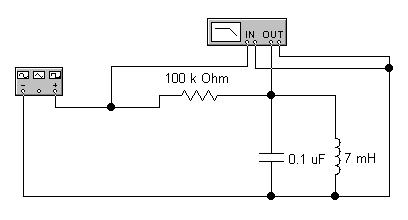
Рисунок 2.15 — Резонансный контур

2.2.8 Отчёт должен содержать результаты выполненной лабораторной работы по всем пунктам методического указания, в том числе заполненные таблицы 2.1 2.2 и 2.3, а также осциллограммы, снятые по пунктам 2.2.2 — 2.2.7.