Математика в памятниках духовного и мирского содержания
В «Книге святых тайн Еноха» даны своеобразная космологическая схема построения мира (описание «четвёртого неба») и некоторые астрономические сведения о движении Солнца и Луны, продолжительности солнечного и лунного года, соответственно 365¼ дня и 364 дня.
В книге Козьмы Индикоплова «Христианская топография» тоже дана система построения материального мира. Светила движутся по небесным кругам. Ему известно о 12 знаках зодиака («домове животни»), то, что в каждом из них Солнце находится месяц, то, что солнечный год (365¼) не равен лунному (364), но это неравенство не объясняется и не исследуется (в отличие от Кирика).
В «Шестодневе» имеется описание размеров Земли, Солнца и Луны (длина окружности Земли =250 000 стадий, диаметр Земли = 80 000, длина окружности Луны – около 120 000 стадий, диаметр Солнца = 50 000 стадий). Эти данные совпадают с данными Эратосфена (III в. до н.э.). (Стадия = 9600 дюймов или ¼ км).
Астрономические и физико-математические сведения «Толковой палеи» ограничиваются повторительным вычислением размеров светил: уточняется диаметр Солнца (3 000 000 стадий).
Из этих и некоторых других источников становится ясно, что в Киевской Руси уже было известно соотношение между длиной окружности и диаметром, т.е. число π =3,125 (Иоанн-экзарх; экзарх – титул главы болгарской церкви).
Одним из мирских рукописных источников является «Русская Правда», сохранившаяся в трёх редакциях:
краткой – 43 статьи (36 содержат сведения о денежной системе, в 7 нет данных по математике),
пространной – 121 статья (68 – сведения о денежной системе, 50 – не содержат сведений по математике),
сокращённой – более позднего периода (≈ XV в., Московская Русь).
Математические сведения, как правило, находятся в статьях с сельскохозяйственным содержанием. Кратко укажем такие сведения:
В некоторых из них содержат задачи весьма сходные с задачей Фибоначчи «о кроликах», приводящей к числам Фибоначчи. Вычисления представляют собой геометрическую прогрессию со знаменателем 2. Эта же прогрессия встречается в задаче о пчёлах.
В других помещены математические выкладки, основанные на системе мер:
1 гривна =20 ногатам = 25 кунам =50 резанам,
1 ногата =1.25 куны = 2,5 резаны.
Еще одна группа – статьи об определении приплода и прибытков – указывает на повышение уровня вычислительной техники по сравнению с современниками Кирика.
Математические знания русских зодчих и ремесленников
Непрямые источники дают, пожалуй, больше сведений для рассматриваемой темы. Русские зодчие приобретали свои знания долголетним ученичеством, самостоятельным опытом и «книжным учением». Бесспорно, что они не только знали свойства материалов и умели соединять их в строительные конструкции, но и обладали некоторой суммой знаний в области арифметики и геометрии:
Зодчие Киевской Руси широко использовали геометрические построения, где важное место имели отношения 1:2, 2:3, 3:4, 4:5, 5:6 и т.д., а также «золотое сечение». Геометрический анализ храма св. Софии К.Н. Афанасьевым, дал следующие результаты: если не учитывать второстепенные детали, то, оказывается, с помощью простейших геометрических построений, исходя из размеров главного купола, можно последовательно определять все остальные размеры храма. Причём эти построения можно произвести и на выровненной площадке, при разбивке сооружения в натуре!
Рассмотрим аддитивный ряд «золотого сечения»: 0; 1; 1; 2; 3; 5; 8; 13; 21; 34; 55;… и отношения между последующими двумя членами:
0; 1; 0,5; 0,667; 0,6; 0,625; 0,6154; 0,619; 0,6176; 0,6182;….
-ый
член которого при
стремится к величине
.
С помощью числа
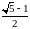можно получить новый числовой ряд:
1; 0,618; 0, 382; 0,236; 0,146; 0,090; 0.056; …,
обладающий следующими свойствами:
сумма каждых двух последующих членов ряда равна предыдущему члену;
каждый член ряда является средним геометрическим предыдущего и
последующего члена ряда.
0,618 0,382 0.618
Оказывается, если квадрат со стороной 1 разделить на два прямоугольника со сторонами 0,618 и 0,382, то площадь второго прямоугольника будет средним геометрическим между площадью первого квадрата и площадью всего квадрата. Отсюда следует, что
отношение площади квадрата со стороной 0,382 к площади квадрата со стороной 0.618 равно 0,382;
объём куба со стороной 0,618 есть среднее геометрическое между объёмом куба со стороной 1 и объёмом куба со стороной 0,382.
Таким
образом, числа 0,618; 0, 382; 0.236 представляют
собой второй, третий и четвёртый члены
ряда. Так вот эти отношения были известны
зодчим Киевской Руси и воплощены в ряде
строительных сооружений. Ими пользовались
при графическом определении основных
размеров здания с помощью пропорционального
циркуля. В ряде построек эти отношения
слегка варьировались, так при строительстве
церкви покрова на Нерли под Новгородом
(1165-1167) в качестве такого основного
отношения было принято
.
Таким
образом, можно отметить значимую
осведомлённость русских зодчих в области
прикладной математики, которые создавали
архитектурные формы с помощью «геометрии
построения» с использованием циркуля
и линейки.
Интересные данные можно получить, исследуя строительные материалы, т.к. условия прочности, технология работ, сама архитектурная форма заставляли соблюдать определённые пропорции при изготовлении кирпича. В XII веке обычными размерами для него были 30,8×22×4,4 см. Для сооружений часто применялся и бутовый камень (золотые ворота и стены Софийского собора в Киеве, старинные церкви в Чернигове). Для перекрытия таких бесформенных камней подходил более тонкий и большего размера кирпич – плинфа, типичный для зданий X-XI века, размерами 40×30×3,5. Изменение характера конструкций повлекло и изменение кирпича, он становится более толстым (30×20×5,5) и приближается размерами к современному (25×12×6,5).
Анализ работ мастеров различных ремёсел позволил тоже выявить владение некоторыми математическими сведениями. В эпоху, предшествующую Киевской Руси гончарное производство вытеснило домашнее, формы кувшинов были очень разнообразны. По эволюции фибул - металлических застёжек – и ташек – пуговиц - можно проследить постепенные изменения геометрических форм (1-я: один полукруглый щиток, второй – ромбовидный; во 2-й: полукруг делится на 5 равных частей, в 3-й – на 8, затем – на 6, затем появляются новые формы, в частности и криволинейные).
Внешний вид очень многих литых предметов и инструментов, найденных при раскопках курганов, X-XIII вв., указывает на знакомство мастеров с простейшими свойствами геометрических фигур. Распространённый в то время способ нанесения орнамента на браслеты, височные кольца производился зубчатым металлическим колёсиком (24 зубчика). Для изготовления этого инструмента нужно было уметь делить окружность на 24 части, ручной гончарный круг и клейма ремесленников имели разнообразные формы (концентрические и соприкасающиеся окружности, квадрат, вписанный в квадрат и пр.). Встречается деление окружности на 4, 6, 8 равных частей.
Весьма разнообразные геометрические формы встречались в литейном, оружейном и кузнечном деле. Например, замок и ключ к нему (части рукояток ключей – в форме цилиндра, призмы и т.д.). Сложными по форме были и русские шлемы, литейщики по восковой модели изготовляли арки, паникадила и пр., золотых дел мастера использовали тоже разнообразные формы. Резюмируя вышесказанное, можно отметить, что мастерам Киевской Руси были известны как плоские геометрические фигуры (квадрат, прямоугольник, параллелограмм, ромб, круг), так и пространственные (куб, параллелепипед, пирамида, конус, шар) и их части, а также деление окружности на 6, 3 и 24 части.