Вопросы и задания

1. Что такое изолиния функции двух переменных?

2. Как выглядит картина изолиний конической поверхности?

3. Чем отличаются между собой типизированные и текстовые файлы? Почему выгоднее хранить массивы вещественных чисел в типизированных файлах? Какие преимущества имеет хранение данных в текстовых файлах?

4. Какие элементы управления Delphi использованы в программе построения изолиний?

5. Изучите процедуру построения изолиний и ответьте на вопросы:

- как определяется положение на холсте и размер области вывода изолиний?

- как вычисляется шаг изменения значений изолиний?

- каким образом вычисляются координаты точек пересечения изолинии с линиями расчетной сетки?

- как происходит пересчет координат пересечения изолиний с линиями расчетной сетки в графические координаты холста?

- как обеспечивается однократный вывод номера изолинии на рисунок?

§3.3.6. Вычислительные эксперименты с построением изотерм

Проведение вычислительных экспериментов для задачи теплопроводности с получением картины изотерм будем осуществлять с помощью программы на Паскале Teplo (см. §3.3.4) и программы на Delphi построения изолиний, приведенную в предыдущем параграфе.

Передача данных между ними осуществляется через файл. Организуем в программе Teplo вывод в файл значений массива T во внутренних ячейках сетки. Для этого добавим в программу следующие операторы, по аналогии с программой Polusfera. В начале программы:

Var Flt: file of real; //файловая переменная

begin

Assign(Flt, 'F:\temp\Tmas.dat'); //Назначение файла

Rewrite(Flt); //Открытие файла для записи

В конце программы:

//Запись массива в файл поэлементно

for i:=1 to M do

for j:=1 to N do write(Flt, T[i,j]);

close(Flt);

Для расчетов будем использовать сетку с параметрами:

Const M=50; N=50;

Вычислительный эксперимент 1: квадратная область; границы с постоянными температурами. Зададим исходные данные такими же, как в §3.2.10, в 1-м вычислительном эксперименте: 1-я граница имеет температуру 0⁰, остальные 100⁰.

Сделаем одно важное замечание. Итерационный вычислительный процесс в программе Teplo будет сходиться от любых начальных значений для массива T. Выбор начального приближения влияет лишь на время сходимости: чем ближе начальное приближение к окончательному результату, тем количество итерационных циклов будет меньше, следовательно, и меньше будет время вычислений на компьютере. В проведенном расчете начальное приближение температуры во внутренних ячейках области было задано равным 50 (среднее между 0 и 100).

При выполнении программы Teplo, ввод исходных данных будет выглядеть так:

T1=0

T2=100

T3=100

T4=100

Eps=0.0001

Max=500

Затем запускаем программу построения изолиний. Результат представлен на рис.3.35.

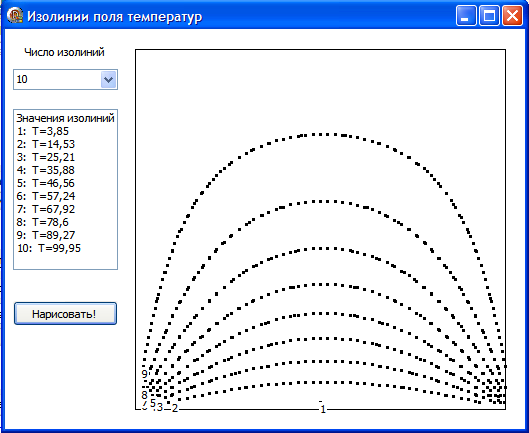
Рис.3.35. Картина изотерм в 1-м эксперименте

Из картины изолиний видно, что наиболее быстрое изменение температуры происходит вблизи нижних углов области. А вблизи верхней границы изменение температуры очень слабое. Там температура близка к граничному значению 100⁰.

Вычислительный эксперимент 2: квадратная область, границы с линейным распределением температур.

Пусть левый нижний и правый верхний углы прямоугольной области поддерживаются при температуре 100⁰, а левый верхний и правый нижний углы - при температуре 0⁰. Изменение температуры вдоль каждой границы происходит равномерно, по линейному закону от 0 до 100.

В программу Teplo нужно внести следующие изменения: вводить только погрешность итераций eps и максимальное число итераций Max; запрограммировать вычисление линейного распределения температуры на границах. Соответствующие разделы программы должны быть следующими:

//Ввод исходных данных

Write('Eps='); readln(eps);

Write('Max='); readln(Max);

//Граничные условия

for i:=1 to M do

begin T[i,0]:=100-100/(M+1)*i; T[i,N+1]:=100/(M+1)*i end;

for j:=1 to N do

begin T[0,j]:=100-100/(N+1)*j; T[M+1,j]:=100/(N+1)*j end;

Вычисления проводились на сетке M=N=50. При выполнении программы вводились исходные данные:

Eps=0.0001

Max=500

Полученный массив температур обрабатывался программой построения изолиний. Результат представлен на рис…..

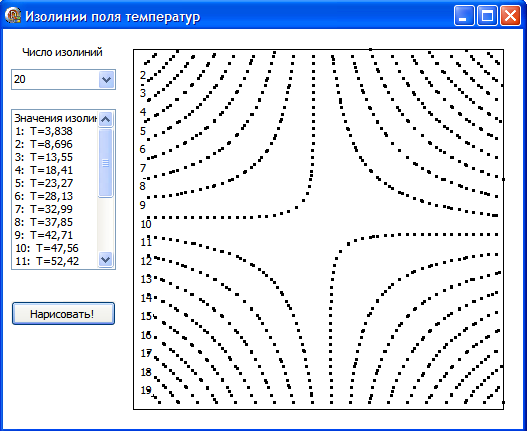
Рис.3.36. Картина изотерм во 2-м эксперименте

В центральной части области температура близка к 50⁰. Симметричность картины изолиний является следствием симметричности граничных условий для температуры.

Вычислительный эксперимент 3: вытянутая прямоугольная область, границы с линейным распределением температур.

В этом эксперименте вертикальный размер области будет в 2 раза больше горизонтального. Поскольку, ячейки расчетной сетки имеют квадратную форму, то для параметров сетки выполняется равенство: M=2N. Выполним расчеты на сетке М=50, N=25. Эти значения нужно установить для соответствующих констант в программe Teplo и в программе построения изолиний.

Как и в предыдущем эксперименте, температура на границах изменяется линейно от 0 до 100 градусов. Поэтому не требуется в программе Teplo изменять расчет граничных условий.

Результат вычислительного эксперимента представлен на рис.3.37.

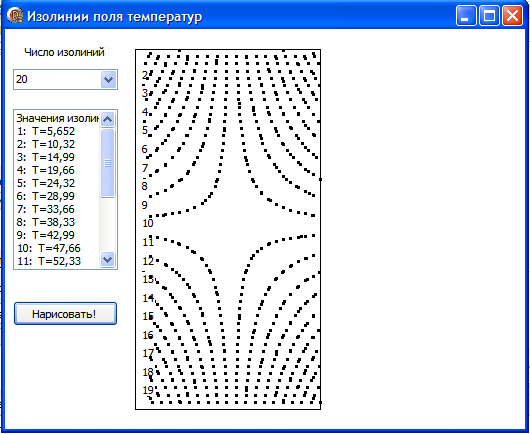
Рис.3.37. Картина изотерм в 3-м эксперименте

В программе построения изолиний предусмотрено изменение размеров окна графического вывода пропорционально размерам расчетной области.