Розв’язування.

Розглянемо рух механічної системи, що складається з тіл 1, 2, 3, 4, з’єднаних нитками. Система має одну ступінь вільності. В’язі, накладені на систему, є ідеальними.

Для визначення прискорення вантажу 3 – використаємо загальне рівняння динаміки:

, (1)

де сума можливих робіт активних сил, що діють на систему; сума можливих робіт сил інерції.

Зобразимо діючі на систему активні сили і пару сил з моментом (рис.Д4.б). Задамо напрям прискорень тіл. Прикладемо сили інерції тіл 3 і 4 ( ), які виконують поступальний рух. Зобразимо момент сил інерції тіла 2 ( ), яке обертається навколо нерухомої осі. Напрямок інерційних сил і моментів - протилежно відповідним прискоренням.

Ч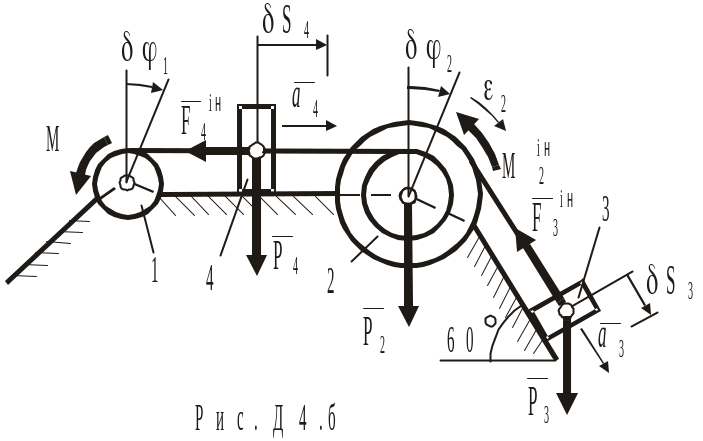 исельно вони дорівнюють:

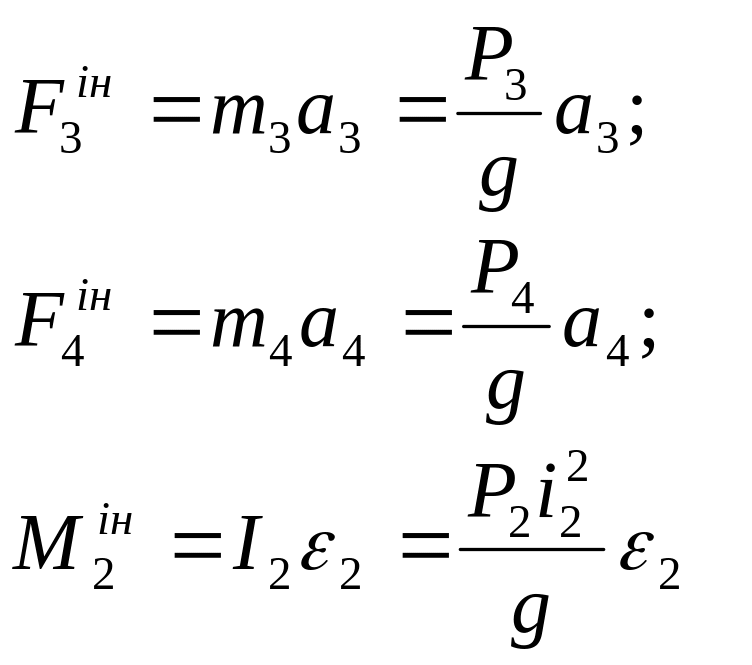(2)

Задамо системі (рис. Д4.б) можливе переміщення та складемо загальне рівняння динаміки для системи:

(3)

Через те, що механічна система має один ступінь вільності, виразимо всі можливі переміщення через одне, наприклад, :

(4)

Підставимо величини (2) та (4) в рівняння (3) і отримаємо:

(5)

Всі прискорення, що входять до (5), виразимо через шукане :

(6)

Враховуючи, що можливі переміщення нескінченно малі, але не дорівнюють нулю ( тобто ) , та враховуючи (6) отримаємо:

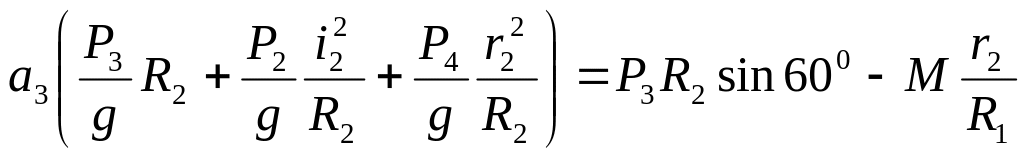(7)

Приймемо , підставимо числові значення та знайдемо :

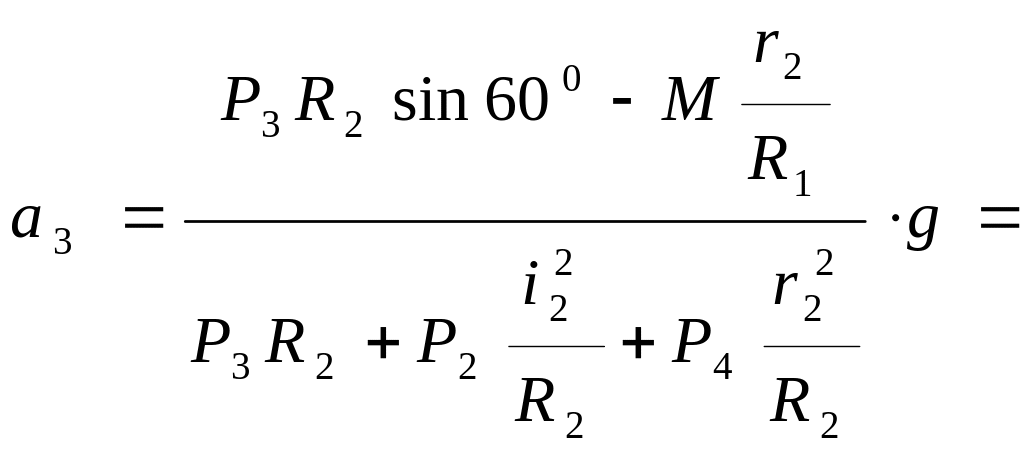
. Знак “-“ указує на те, що прискорення вантажу 3 та прискорення інших тіл системи спрямовані протилежно показаним на рис. Д4.б.

.

Відповідь:

6. Література

1. Освітньо-професійна програма вищої освіти за професійним спрямуванням “Інженерна механіка”. – Київ, МОН України. - 1994 р.

2. Теоретическая механика: Методические указания и контрольные задания для студентов-заочников машиностроительных, строительных, транспортных, приборостроительных специальностей высших учебных заведений / Л.И.Котова, Р.И.Надеева, С.М.Тарг и др.; Под ред. С.М.Тарга - М.: Высш.шк., 1989.-111 с.

3. Теоретическая механика: Методические указания и контрольные задания для студентов-заочников энергетических, горных, металлургических, электроприборостроения и автоматизации , технологических специальностей, а также геологических, электротехнических, электронной техники и автоматики, химико-технологических и инженерно-экономических специальностей вузов / Под ред. С.М.Тарга. – М.: Высш. шк., 1988. – 64 с.

4. Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике. – 1985.

5. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов. – М.: Высш. шк., 1986. – 416 с.

6. Добронравов В.В., Никитин Н.Н. Курс теоретической механики: Учебник для машиностроит. спец. Вузов. – М.: Высш. школа, 1983. – 575 с.

7. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Ч.I. Статика. Кинематика. Учебник для втузов. М., «Высш. школа», 1977.- 368 с.

8. Яблонский А.А. Курс теоретической механики. Часть II. Динамика. Учебник для втузов. М., «Высш. школа», 1984. - 423 с.

9. Діденко Г.О Настановні лекції з теоретичної механіки ( для студентів-заочників немеханічних спеціальностей ). - Маріуполь, ПДТУ, 2001.- 38 с.

10. Діденко Г.О. Методичний навчальний посібник з розв’язування задач теоретичної механіки ( Розділи: Статика, Кінематика ) для студентів напрямку підготовки 0902 – „ Інженерна механіка”. – Маріуполь, ПДТУ, 1998.

11. Діденко Г.О. Телевізійна лекція „ Силові характеристики геометричної статики і операції з ними”. – Маріуполь, ПДТУ, 2003.

12. Діденко Г.О. Телевізійна лекція „ Рівняння рівноваги системи сил та їх використання у задачах геометричної статики”. – Маріуполь, ПДТУ, 2003.

13. Карпенко Т.М. Конспект лекцій з теоретичної механіки. Динаміка.- Маріуполь, ПДТУ. – 2004, (www.pstu/l_u/metod/mm/TiPM/index.html).

14. Винникова В.Г. Телевизионная лекция «Кинетическая энергия и ее изменение». Части 1 и 2. - Маріуполь, ПДТУ, 2003, (www. pstu. edu./ У допомогу студенту/ Інше/ Лабораторія учбового телебачення).

15. Карпенко Т.М. Телевізійна лекція „ Динаміка механічної системи”. Частини 1 і 2. – Маріуполь, ПДТУ, 2004, (www. pstu. edu./ У допомогу студенту/ Інше/ Лабораторія учбового телебачення).

16. Карпенко Т.М. Телевізійна лекція „ Способи складання динамічних рівнянь руху практичних моделей механічної системи”. – Маріуполь, ПДТУ, 2004, (www. pstu. edu./ У допомогу студенту/ Інше/ Лабораторія учбового телебачення).

17. Карпенко Т.М. Телевізійна лекція „ Принципи механіки”. – Маріуполь, ПДТУ, 2004, (www. pstu. edu./ У допомогу студенту/ Інше/ Лабораторія учбового телебачення).

 Можливі ступені вільності , заборонені ступені вільності

 У деяких випадках для визначення рівняння траєкторії руху точки зручно використо-вувати тригонометричні формули:

70