61. Модель очередей к одному серверу. Параметры очередей (см.73). Характеристики моделей.
Формулы используют следующие допущения:
частота поступления запросов подчиняется распределению Пуассона;
дисциплина диспетчеризации не дает предпочтения запросам, основываясь на времени обслуживания;
в формулах для среднеквадратичного отклонения предполагается диспетчеризация FIFO;
запросы не выбрасываются из очереди.
Модель M/G/1.
Интервалы времени обслуживания подчиняются произвольному распределению. Использование коэффициента масштабирования А позволяет упростить формулы для некоторых ключевых выходных переменных. Обратите внимание на то, что масштабирующий коэффициент зависит от отношения среднеквадратичного отклонения времени обслуживания к среднему значению. Никакой другой информации о времени обслуживания не требуется. Итак, формулы для произвольного распределения времени обслуживания:
;
;
;
;
.
Модель M/M/1.
Среднеквадратичное отклонение равно среднему значению, распределение времени обслуживания является экспоненциальным (М/М/1). Это простейший случай, в котором легче всего получить результаты. Далее показаны упрощенные варианты формул для среднеквадратичного отклонения r и Tr а также некоторые другие интересные соотношения:
;
;
;
;
;
;
;
;
;
;
.
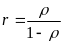M/D/1.
Cреднеквадратичное отклонение времени обслуживания равно нулю, что означает постоянное время обслуживания :
;
;
;
;
;
.
62. Модель очередей к нескольким серверам.
Ниже перечислены формулы для некоторых ключевых параметров случая нескольких серверов. Ряд ограничений накладывается в допущениях:
частота поступления запросов подчиняется распределению Пуассона;
значения времени обслуживания распределены экспоненциально для всех серверов;
все серверы загружены в равной мере;
среднее время обслуживания всех серверов одинаково;
используется диспетчеризация FIFO;
запросы не выбрасываются из очереди.
— функция
отношения Пуассона;
— С-функция
Эрланга;
;
;
;
;
;
;
;
;
.
Обратите внимание на присутствие С-функции Эрланга практически во всех уравнениях. Она означает вероятность того, что в данный момент времени заняты все серверы. Другими словами, это вероятность того, что количество запросов в системе (ожидающих и обслуживаемых) больше или равно количеству серверов. Соответствующее уравнение имеет вид
.
Здесь К — функция отношения Пуассона. Поскольку величина С представляет собой вероятность, эта величина всегда находится в диапазоне от 0 до 1. Как можно видеть, она является функцией от числа серверов и коэффициента использования. Это выражение часто встречается при расчетах очередей. Можно воспользоваться готовыми табличными значениями или компьютерной программой. Обратите внимание на то, что для системы с одним сервером эта формула упрощается до С( 1, ρ) = ρ.
63. Очереди к серверам с приоритетами.
Общие формулы:
;
;
;
;
;
.
Теперь формулы для случая, когда время обслуживания распределено экспоненциально:
;
;
;
.