1.6 Перечень наиболее эффективных способов механической обработки основных рабочих поверхностей типовых деталей, полученных в результате системного поиска решений на эвм, в сравнении с традиционными

При реализации вышеизложенного алгоритма на ЭВМ ЕС для определения трех наиболее эффективных схем формообразования, задавалась поверхность детали, как поверхность вращения (вала или отверстия),

Расположенного в системе координат Zo Xo Yo с осью вращения Оо Xo, алгебраическим выражением вида:

(1.22)

В качестве режущей кромки брали ломанную линию (схематизация кромки проходного резца), которая была задана параметрическим уравнеинем точки в системе координат инструмента:

(1.23)

Геометрическая интерпритация трех наиболее производительных схем формообразования, найденных ЭВМ, по полученной печати параметров имеет следующий вид: схема А) ПР=100000 КТ, схема б) ПР=100000 КТ, схема в) ПР=100000 КТ.

А)

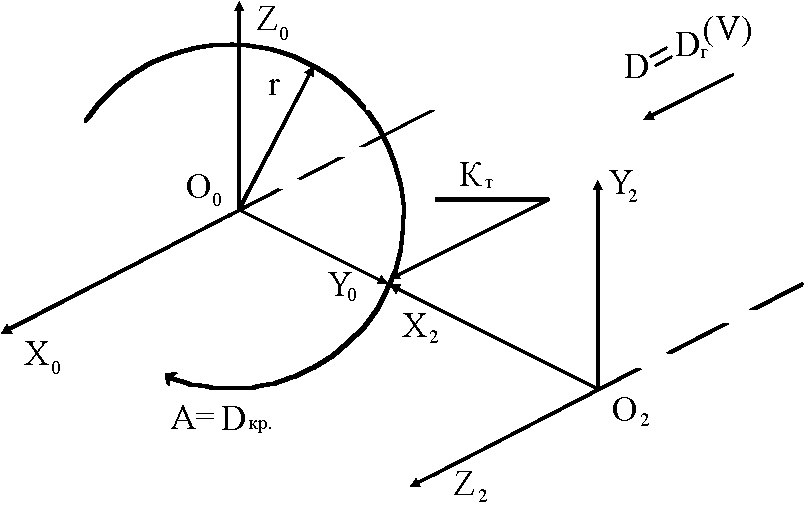
б)

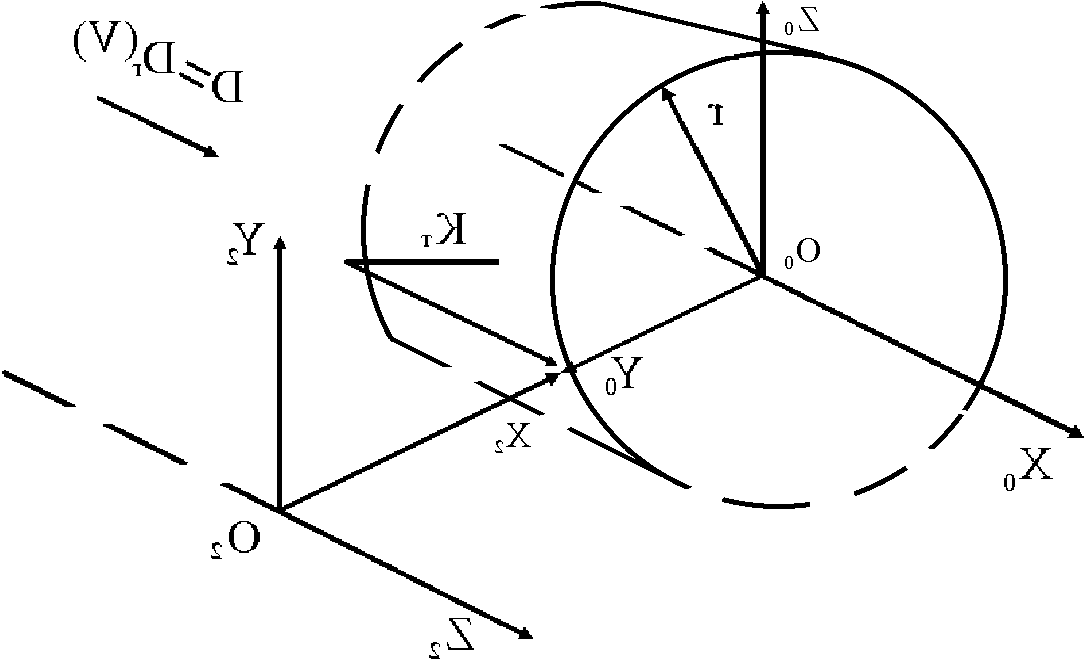
в)

Рис.1.10

Из рис.1.10 следует, что в схеме а) главное движение резания вращения детали вокруг оси ОО ZО; подача вдоль оси ОО ХО || О2 Z2 есть вспомогательное движение - Ds. Производительность, оценивается количеством точек, расположенных на теоритически заданой поверхности детали с постоянным шагом - К Т =

Такая же производительность у схемы б), у которой главное движение резания линейное движение D _Г по оси O2 Z2 || ОО Х2 , а вращение А круговая подача, т.е. вращение детали вокруг своей оси.

Самая низкая производительность у схемы в) ПР ≈ кт . Эта схема включает только одно движение резания линейное перемещение со скоростью резания вдоль O2 Z2 || Оo Х2 D _Г= Dг = ƒ(V).

Анализ схем весьма прост. Схема а) легко трансформируется в способ точения:

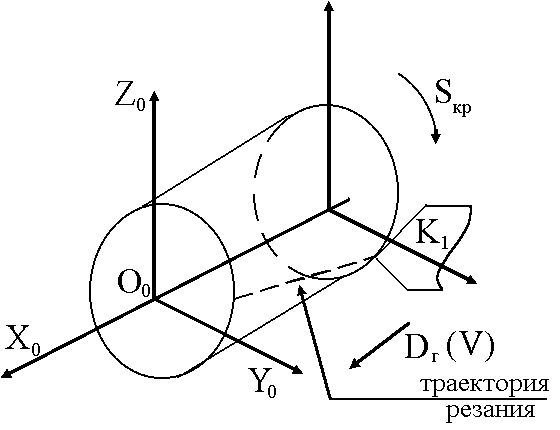
б)

а).

.

в)

Рис.1. 11

Схема б) в способ строгания с круговой подачей, выполняемой непрерывно. Схема в) в способ строгания без непрерывной подачи.

По данным многих исследований, все схемы имеют интерес и используются в производстве в виде операций: точения и растачивания - способ а); долбления с одновременной круговой подачей - схема б) и с циклической подачей на 1 двойной ход схема в). Наибольшее распространение схемы б) и в) получили при протягивании отверстий прогрессивным методом удаления припуска.

При задании режущей кромки как винтовой линии ЭВМ позволила так же определить три кинематические наиболее производительные схемы:

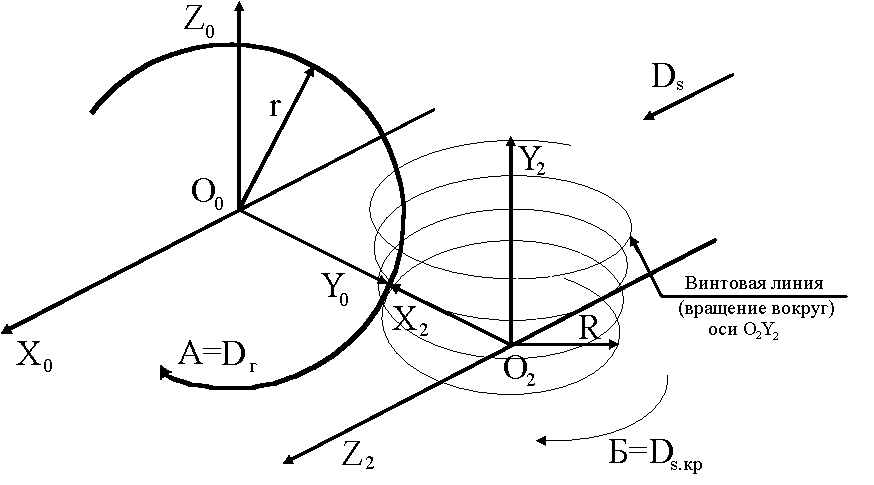
а)

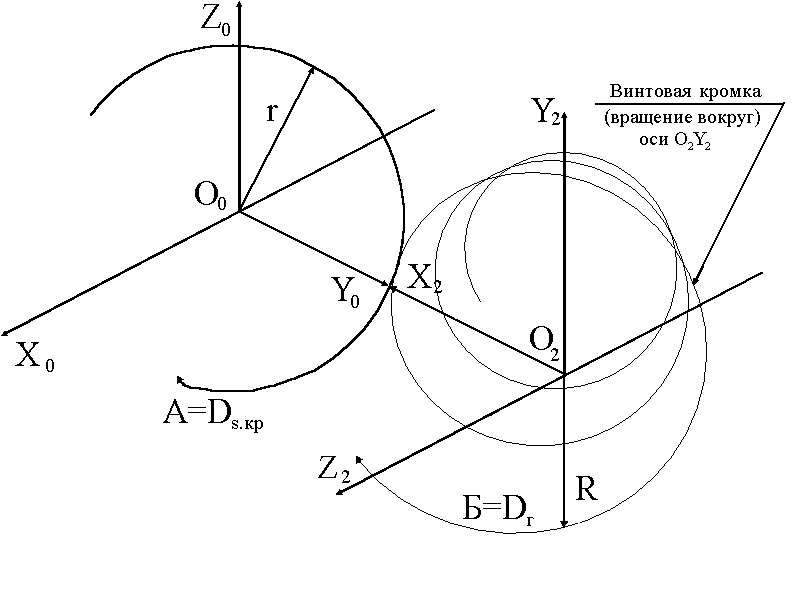
б)

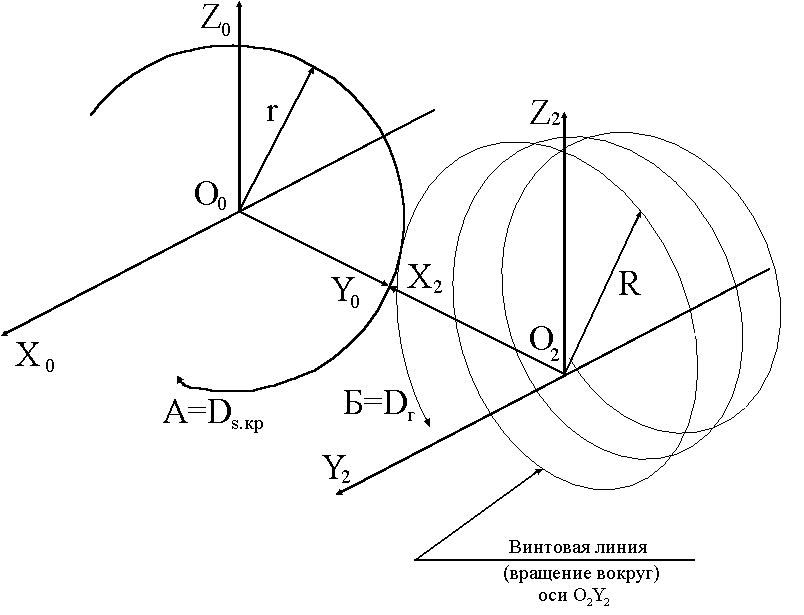
в)

Рис. 1.11

На Рис. 1.11 схема а) формообразования винтовой режущей кромкой на поверхности вращения вокруг оси О2 Y2 с радиусом R имеет главное движение резания - вращения поверхности вокруг собственной оси - А и две подачи: вдоль оси Оо Хо || О2 Z2 О2 Y2 - оси вращения линии режущей кромки как винтовой цилиндра:

-подачи - Ds и круговой подачи B = Ds кр самовращение винта кромки (Пр = 8* кт). На б) главным движением резания является движение вращения винта режущей кромки вокруг собственной оси.B = Dг. Движение вращения обрабатываемой поверхности вокруг собственной оси является движением круговой подачи А = Ds кр.

На в) главным движением резания является движение B = Dг, но оно в отличие от схемы находится в плоскости перпендикулярной плоскости вектора А и основанном на трех движениях А = Ds кр,

B = Dг = ƒ(V) и Ds пр

Поскольку схемы а) и в) имеют одинаковые расположения винта инструмента, а схема б) повернутое на 180° от указанных той геометрическая интерпретация способов так же очевидна:

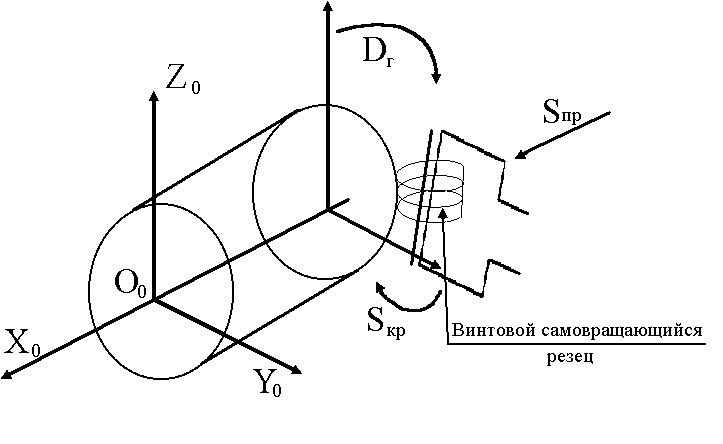
а)

б )

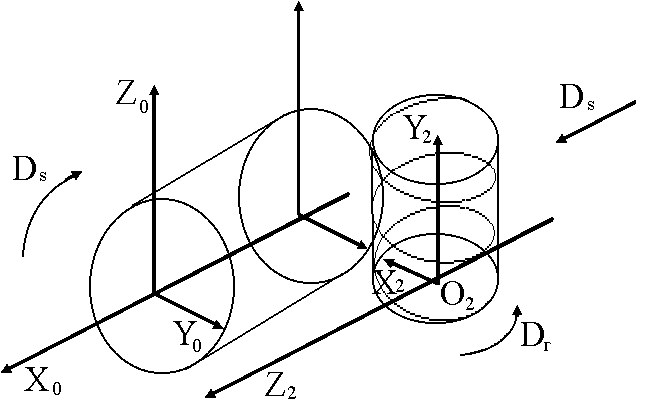
в)

Рис.1. 12

Изображенные на рис.1.12 схемы соответствуют: а) - схема точения самовращающимися резцами с винтовой режущей кромкой, на данный способ получена Ав. св. СССР 1976 г. При придставлениии поверхности детали как наружной поверхности вращения ЭВМ предлагает схему фрезерования по методу обкатки с продольной подачей как наиболее производительную по кинематическому критерию. На нее также получено авторское св. СССР.

При задании обработанной поверхности как плоскости Xo = 0 ; Yo = Zo = - ∞ до +∞

Vp = f (n_u)

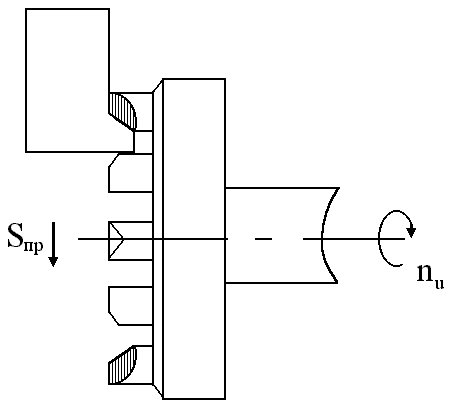
V

a)

p = f (n_u)

Рис.1.13 (начало)

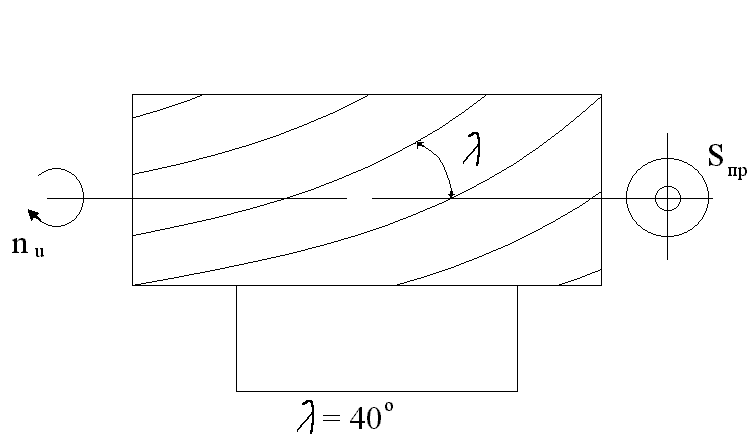
в)

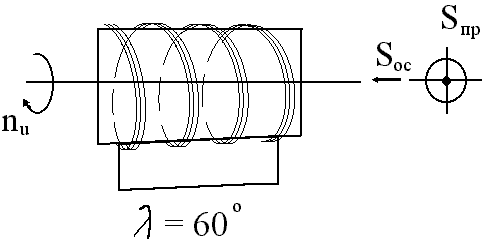
Рис.1.13 (продолжение)

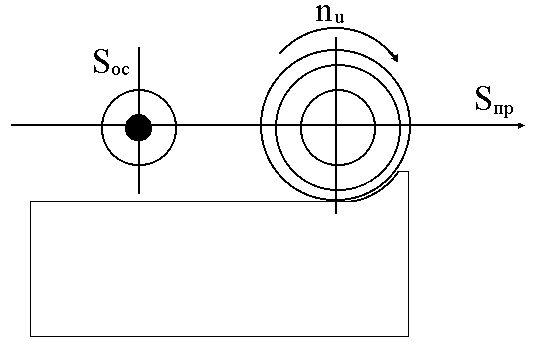
Vp = f (n_u ,S_oc)

c)

Рис.1.13 (окончание)

При представлении обрабатываемой поверхности, у которой образующей в системе координат ZoYoXo в плоскости ZoOoYo является эвольвента заданная натуральным уравнением:

или

П

олучены следующие способы формообразования эвольвентные поверхностей прямозубых колес, представленных на рисунках 1.14, 1.15., 1.16, а так же третьим способом был процесс известный всем, как зубофрезерование червячными фрезами.

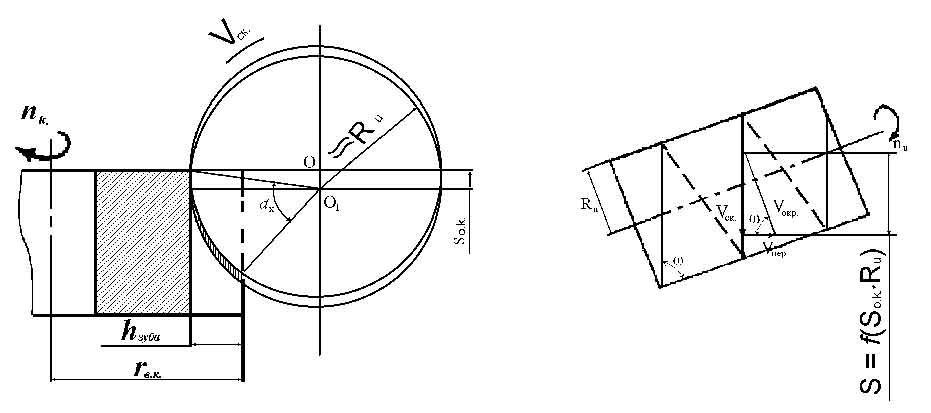
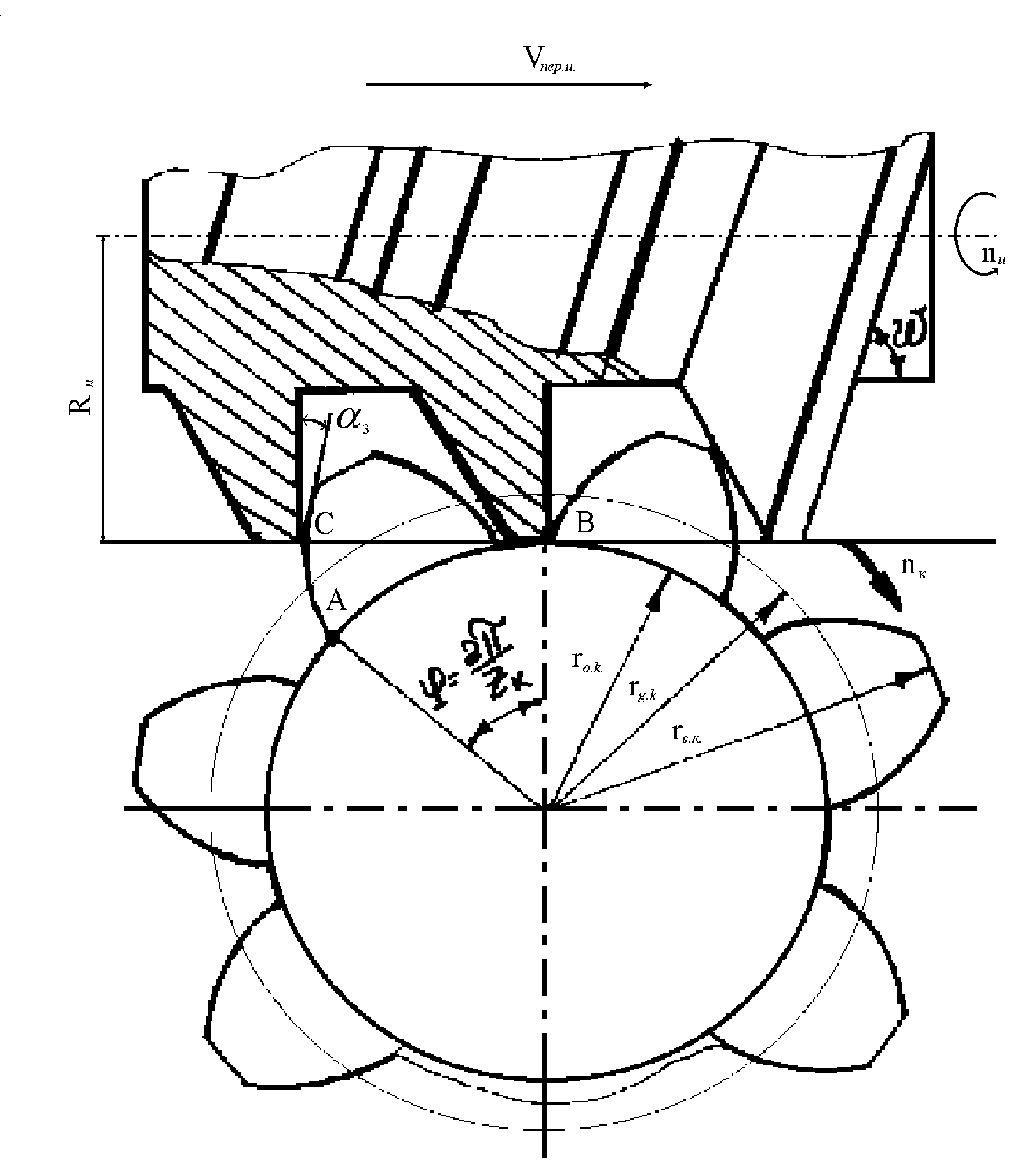
Рис1.14 Кинематическая схема формообразования эвольвентой поверхности точкой винтовой линии.

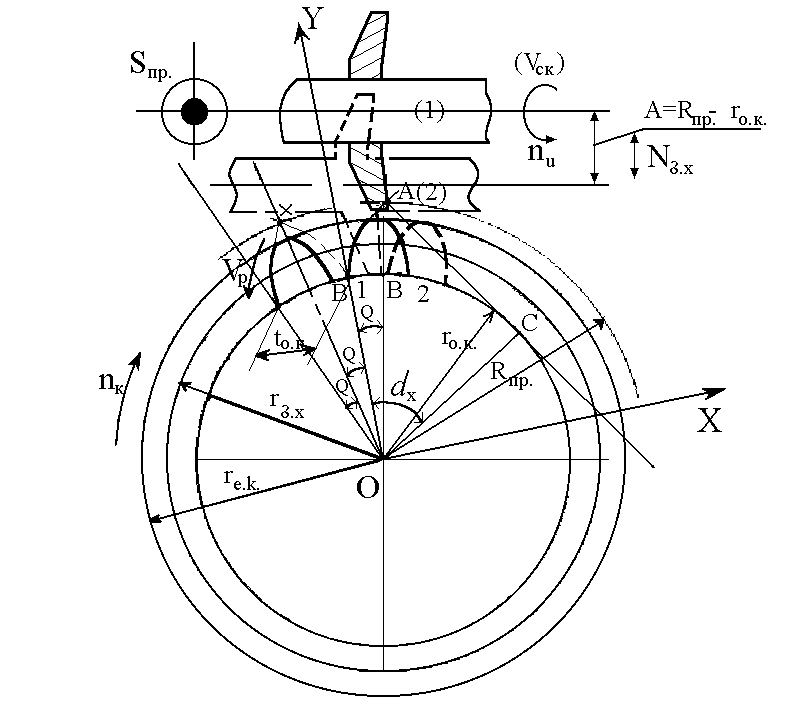
Рис. 1.15

ρ = АО = r_o.к. t _o.к. = π*m*cos20°

АС = r _o.к. [ -1], если: r _o.к.* . = π*m*cos20°≥h зуба

-- условие формообразования Q = - arctg( )

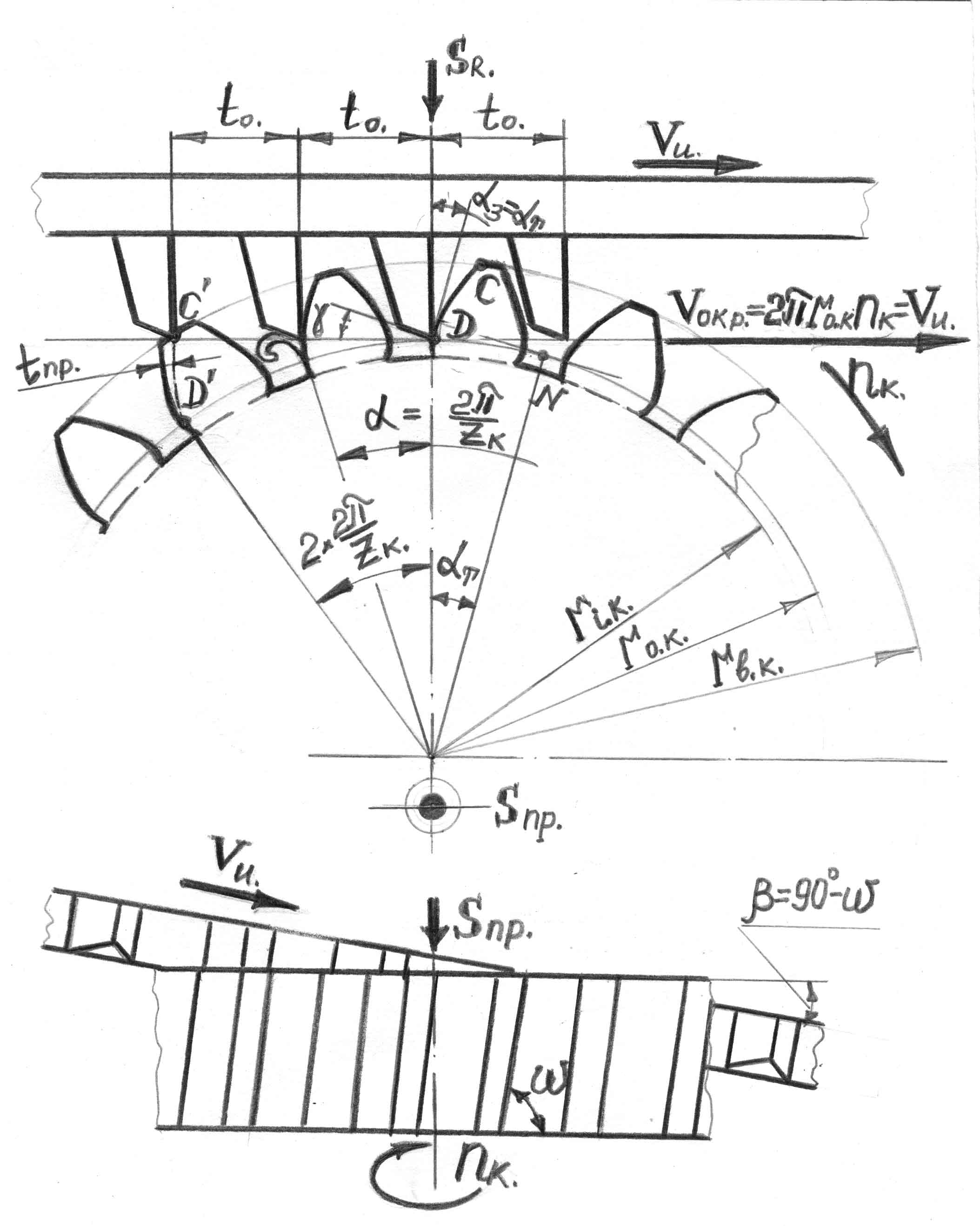
Рис.1.16

Приведенные схемы формообразования защищены авторскими свидетельствами и патентами РФ. Таким образом, алгоритм позволяет решать задачу поиска новых способов механической обработки системно и на уровне изобретений [24,39,46,66,67,68,72,75,76,].