I.5 Методика трансформации найденной схемы формообразования заданной поверхности в способ механической обработки

Из анализа описания алгоритма поиска схем формообразования поверхностей инструмента и определения трех наиболее эффективных следует:

а) Инструмент не определен, но задан формой линии его режущей кромки и радиусом её расположения если , а движение B как вращательное есть B=ƒ(v), что выводится на печать ЭВМ.

б) Если радиус инструмента , а его кромки представлены линией окружности и при этом на печать выводится условие B=ƒ(v), А= ƒ(v) , то из этого следует, что схема формообразования соответствует точению, а инструмент ротационный резец. В противном случае: В≠ ƒ(v), А= ƒ(v) . Процесс соответствует фрезерованию, а инструмент - фреза, что также предусмотрено алгоритмом.

Таким образом, трансформация схемы формообразования определенной на ЭВМ как наиболее эффективная весьма проста. Поскольку печать ЭВМ конкретизирует движения, выполняемые в процессе формообразования, устанавливает равенство или неравенство нулю . Определяет форму режущей кромки инструмента как линию и только в случае режущей кромки как пересечение двух линий (резец с углами в плане) представляет ее точкой. Поскольку трансформация информации полученной с ЭВМ в способ является простым изображением процесса как схемы резания со словесной констатацией типа инструмента:

а) фреза (B=ƒ(v),R _и ≠0);

б) резец простой

в) резец ротационный (B=ƒ(v),R _и ≠0,В≠0);

г) фреза с винтовым зубом при конкретном значении угла подъема ее винтовой линии режущей кромки напримерW=60⁰;ƒ(Р)=R _и ∙sin(Р∙α); .

Наиболее сложные случаи трансформации схемы формообразования в способ механической обработки возникают при выводе на печать условий определяющих движение со скоростью резания как результирующее, являющееся производным от двух выполняемых движений. Например: режущая кромка задана в виде винтовой линии с углом подъёма от оси вращения - произвольная величина. На печать выводится как самая производительная схема формообразования, эвольвентой поверхности прямозубого колеса схема содержащая три движения А≠0, В≠0,DY=0. При их выполнении на скрещивающихся осях, когда угол поворота , винта кромки инструмента. При этом скорость резания V=ƒ(АиВ). В этом случае возникает несколько решений при трансформации схемы в способ формообразования. Чтобы избежать их требуется проанализировать процесс формообразования эвольвентой поверхности прямозубого колеса при задании линии кромки инструмента точкой и затем его кромки в виде окружности радиуса .

Данная операция поможет установить те схемы резания, которые вытекают из первой сложной, с винтовой линией режущей кромки, при вращении которой существует переносное движение. Оно и будет найдено по величине если кромку представить точкой. Все схемы будут соответствовать зуботочению вдоль эвольвенты. Только в первом случае данное зуботочение будет осуществляться фрезой, что легко устанавливается графической интерпретацией полученной с ЭВМ информации о наиболее эффективном способе формообразования.

В заключение следует констатировать, что метод трансформации схем формообразования в способы по данным, получаемым при печати на ЭВМ, весьма прост. Есть метод графического представления схемы относительного расположения обрабатываемой поверхности детали и режущей кромки инструмента с указанием векторов выполняемых перемещений, на которых главное движение резания обозначается значком r в соответствии с ГОСТом.

Если в схеме(- способе) задана одна режущая кромка как линия, а при графической интерпретации схемы формообразования станет очевидным применение и нескольких таких кромок (имеется в виду фрезы с большим числом заходов), то процесс трансформации позволяет получить из одной схемы формообразования два или несколько способов механической обработки, целесообразность использования которых, должна уже определяться практикой или физикой резания, которой будут посвящены дальнейшие исследования, изложенные в последующих главах.

Рассмотрим пример:

Если для поиска возможных схем формообразования, номинальная поверхность детали задана алгебраическим уравнением:

то это есть поверхность вращения сориентированная в системы координат детали так, что её направляющая линия - окружность соответствует плоскости YOZ основной системы координат с радиусом , заданным конкретным числовым значением =10.

Инструмент также предварительно задается как линия или точка в собственной системе координат:

т.е. точка на радиусе

После поиска ЭВМ (как один из найденных вариантов) печатает следующие параметры схемы формообразования, включая ранее заданные:

Частная кинематическая схема формообразования, полученная из общей показана на Рис.1.9

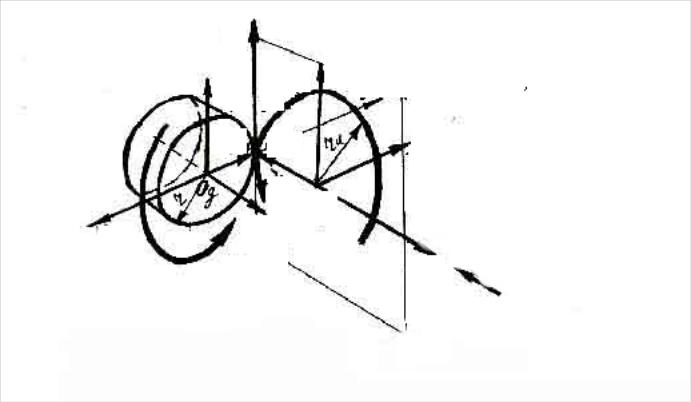
Рис.1.9