I.3. Общие параметрические уравнения для поверхностей резания.
Изображенная на рис.I.7 схема определяет существование абсолютных равномерных движений A, B, DX, DY, DZ, сообщаемых в процессе обработки инструменту и детали механизмом станка. Такое представление схемы соответствует понятию принципиальной кинематической схемы резания - предложенному в работе [19]. Используя данное понятие, следует подразумевать, что перемещения режущих кромок при обработке поверхности детали, вызванные конструктивными особенностями инструмента, кинематической схемой не учитываются.
В настоящей работе понятие - кинематическая схема резания - используется шире. Определение - кинематическая схема резания - используется как тождественное кинематической схеме формообразования. Поэтому схема, изображенная на рис.1.7 , может рассматриваться как конкретная схема формообразования заданной поверхности детали:
если выбраны величины пространственных углов, косинусы которых определяют положение системы координат инструмента относительно системы детали так, что контактная (профилирующая) точка режущей кромки в начальный момент формообразования находится в точке О, которая в свою очередь является точкой теоретически заданной (номинальной) обрабатываемой поверхности детали при принятой схеме базирования детали в системе .
б) если известно количество абсолютных движений; выбрано их направление, а численное соотношение перемещений в направлении указанных на схеме движений таково, что режущая кромка (или линия), перемещаясь по траектории рабочего движения, в процессе формообразования будет занимать такое положение в пространстве, при котором осуществится её постоянное (или периодическое) касание с номинальной - теоретически заданной - формируемой поверхностью.
Иными словами, общая кинематическая схема позволяет рассматривать процесс формообразования какой-либо поверхности детали как перемещение линии по линии. Линии режущей кромки по траектории рабочего движения формообразования. При этом холостые вспомогательные движения инструмента не учитываются. Для некоторых способов формообразования существование этих движений просто необходимо и его следует подразумевать.
Таким
образом, общая кинематическая схема
может определять любую частную схему
формообразования из весьма большого
множества возможных, если известно
уравнение обрабатываемой поверхности
детали при принятой схеме базирования.
Для вывода уравнений формообразующих
поверхностей резания в общем виде (т.е.
обрабатываемая поверхность и схема
базирования детали произвольны, а
конструкция инструмента неизвестна)
конкретизация схемы (рис.1.7) по параметрам,
определяющим поверхность детали и её
положение в системе
,
не должна иметь места. В связи с этим,
используя основные положения теории
формообразования инструментами,
изложенные в соответствующей главе
работы [100] , покажем, что все процессы
формообразования различных поверхностей
деталей режущими инструментами имеют
кинематическое единство и могут быть
рассмотрены в общем виде при использовании
наиболее важных кинематических схем
резания или схем формообразования.
Согласно
упомянутой теории, любая номинальная
поверхность детали может быть определена
двумя линиями криволинейных координат
q
и n
, которые для одной и той же поверхности
можно выбрать в весьма широких пределах.
Будем рассматривать процесс формообразования
поверхности множеством
и кромок. Тогда, с геометрических позиций,
множество кромок может быть определено
в системе инструмента также линией
криволинейной координаты
,
а производящая поверхность инструмента
будет задана двумя линиями криволинейных
координат
и e
, где e
- есть ни что иное, как линия режущей
кромки. Линия криволинейной координаты
производящей поверхности инструмента
выполняет функцию абсолютного рабочего
движения формообразования, т.е.
обеспечивает дополнительное перемещение
кромки относительно формируемой
поверхности детали. В нашем случае закон
расположения кромок на производящей
поверхности инструмента примем
неизвестным и функцию перемещения точки
кромки по линии криволинейной координаты
будет выполнять кинематическая схема
формообразования.
Режущий инструмент обрабатывает поверхность контактным способом, поэтому перемещение режущей кромки в процессе формообразования должно быть связано с таким рабочим движением, при котором обеспечивается хотя бы периодическое касание номинальной поверхности детали. С другой стороны, для выполнения функции резания припуска движение кромки должно быть таким, чтобы припуск на номинальной поверхности детали срезался слоями, по заданному закону. В связи с этим, для удаления всего припуска инструмент должен сделать серию движений резания, благодаря которым, его режущая кромка (или кромки производящей поверхности инструмента, расположенные по линии криволинейной координаты ) создает семейство поверхностей резания, где каждая последующая поверхность резания смещена относительно предыдущей. Движение инструмента, вызывающее такое смещение поверхностей резания, называется подачей, поэтому параметр подачи является параметром семейства поверхностей резания.
Инструмент может иметь несколько подач. Каждая подача вызывает образование семейства поверхностей резания. При большом числе подач режущая кромка инструмента может создать очень сложную систему семейств поверхностей резания. При любой подаче такой системе для процесса формообразования поверхности имеют значения только те подачи, которые определяют перемещение по номинальной поверхности детали точки касания режущей кромки при образовании семейств поверхностей резания. Закон, по которому создана система одного или нескольких семейств поверхностей резания, определяет схема резания или схема формообразования. В данном случае мы будем рассматривать результирующее движение формообразования, указанное на кинематической схеме как определяющее перемещение контактной точки по номинальной поверхности детали при образовании семейств поверхностей резания и отдельных поверхностей семейств.
Сложность кинематической схемы формообразования определяется количеством подач инструмента. Наиболее сложная схема формообразования может определять множество способов обработки заданной поверхности детали при ее трансформации к частным схемам.
Например: если режущая кромка инструмента совпадает (точнее конгруэнтна) с выбранной на номинальной поверхности детали какой-либо криволинейной координатной линией q (или n) , то для формирования поверхности достаточно одно движения резания при отсутствии каких-либо подач. (Здесь возможен вариант определяющий "холостую" подачу, т.е. существование вспомогательного перемещения инструмента по линии координаты q, если линия кромки за одно движение резания не перекрывает ее по протяженности на поверхности детали). В данном случае движение кромки по линии координаты n (или q) называется простым движением резания, так как для формирования номинальной поверхности детали и выполнения второй функции инструмента - снятия припуска - достаточно изменения лишь одного параметра движения.
Если есть необходимость существования "холостой подачи", то её выполняет вспомогательное движение, которое схемой формообразования не учитывается и его следует отнести к транспортному движению инструмента. Та же поверхность детали может быть получена, если инструмент кроме движения резания имеет одну подачу. В этом случае номинальная поверхность детали является огибающей однопараметрического семейства поверхностей резания.
Инструмент имеет две подачи. Номинальная поверхность детали является огибающей двухпараметрического семейства поверхностей резания; является огибающей поверхностью системы семейств поверхностей резания, построенных при наличии трех параметров семейств (трех подач), четырех подач и т.д.
Для всех этих случаев форма режущей кромки может быть выбрана по трем вариантам: линия кромки лежит на номинальной поверхности детали, является касательной к номинальной поверхности; есть произвольная линия (выпуклая или вогнутая, ломаная), форма которой определяется по соображениям облегчения удаления припуска, но она должна быть выбрана так, чтобы в процессе формообразования пересечение номинальной поверхности детали линией кромки не произошло.
Кроме того, формообразование номинальной поверхности детали как огибающей семейства поверхности резания может быть осуществлено двумя способами. При последовательном выполнении движений - резания и подач и одновременном. Если в процессе формообразования одновременно изменяются параметры движения резания и подач (одной или нескольких), то результирующее рабочее движение режущей кромки называют сложным движением резания. При последовательном выполнении движений кромка выполняет указанное выше простое движение резания при неизменности параметров подач, которые изменяются при осуществлении последующего движения формообразования и направления подач.
Для формообразования номинальной поверхности детали безразлично, какое движение резания осуществляет инструмент - простое или сложное. Но в то же время, формы поверхности резания, образованные при простом и сложном движении режущей кромки, будут несколько отличаться друг от друга и в соответствии с этим будут отличаться размеры срезаемых слоев припуска. Однако известно, что это отличие является практически незначительным и им обычно пренебрегают при расчетах схем резания. Впоследствии сделана численная оценка этого изменения, которая подтверждает справедливость сделанного утверждения.
Таким образом, на основании положений теории формообразования поверхностей инструментами и выводов, сделанных в процессе изложения, следует.
Если общая кинематическая схема резания (рис.1.7) определяет процесс формообразования поверхности при осуществлении сложного движения резания, тогда траектория движения контактной точки О может быть представлена однопараметрической зависимостью в общем виде. Параметром данной зависимости может являться величина, определяющая перемещение точки О режущей кромки в результате выполнения абсолютного движения резания. Эта величина связывает по времени моменты касания режущими кромками номинальной поверхности детали и, следовательно, параметры движений подач - есть функции параметра движения резания.
Следует отметить, что, согласно свойствам поступательного и вращательного движений твердого тела, уравнение движений контактной точки О является общим законом движения режущей кромки как твердого тела.
Траектория, образованная на номинальной поверхности детали как след или множество точек от контакта с режущими кромками при движении формообразования, (заданного кинематической схемой резания), может быть рассмотрена как любая криволинейная координатная линия номинальной поверхности q (или n). Следовательно, выбирая абсолютное движение резания и движения подач на общей схеме резания (рис.1.7), процесс формообразования номинальной поверхности детали с геометрических позиций можно рассматривать в общем виде, определив в системе координат произвольные линии криволинейных координат q и n.
Известно, что некоторые поверхности могут иметь криволинейную координатную линию, которая замыкается в пространстве на самой поверхности (как, например, винтовая линия тел вращения). Такую криволинейную координатную линию номинальной поверхности принято называть образующей обрабатываемой поверхности. Траекторию рабочего сложного движения резания, очерченную контактной точкой при формообразовании номинальной поверхности по её образующей, будем называть образующей поверхности резания.
Образующая номинальной поверхности детали всегда является такой линией, точки которой на номинальной поверхности могут быть представлены в любом порядке и следовательно, определять любые линии криволинейных координат q и n.
Для формообразования произвольной номинальной поверхности безразлично, является ли траектория точек контакта с номинальной поверхностью ее образующей или простой криволинейной координатной линией q (или n), так как в том и другом случае должно существовать движение, определяющее формирование соседнего семейства поверхностей резания по второй криволинейной координатной линии n. Единственным отличием этих вариантов формообразования является лишь то, что в первом случае движение формообразования будет непрерывным, а во втором прерывистым последовательным, т.е. необходимо обратно поступательное движение инструмента и последовательное выполнение подачи по линии координаты n. Кроме того, во втором случае будет отсутствовать запись по времени между формированием двух соседних семейств поверхностей резания. При записи уравнений поверхностей резания в общем виде указанное несоответствие само исключается, но оно должно быть учтено при конкретизации общей схемы резания для заданной поверхности детали посредством присвоения произвольной соответствующей подачи расчетного значения, учитывающего или не учитывающего указанную связь по времени.
Таким образом, будем рассматривать процесс формообразования произвольной номинальной поверхности детали при условии выполнения сложного движения резания и существования для номинальной поверхности детали ее образующей.
Для этого в общей кинематической схеме резания (рис.1.7) будем считать заданной произвольную номинальную поверхность при помощи её образующей. Её фиксирует в исходной системе координат детали исходная контактная точка О, положение которой при произвольном базировании детали относительно режущей кромки инструмента задано величиной r.
Если
конструкция инструмента неизвестна,
положение контактной точки режущей
кромки инструмента в её системе координат
будем считать зафиксированным в исходный
момент формообразования произвольным
отрезком
.
За абсолютное движение резания примем движение вращения В. Тогда движение А, DX, DY, DZ будем рассматривать, соответственно, как движения круговой и трех прямолинейных подач в сложном движении резания.
Процесс формирования участка произвольной номинальной поверхности детали с геометрических позиций рассмотрим как пересечение (расположенных как угодно близко по образующей поверхности детали) пары поверхностей резания первого семейства поверхностей и как пересечение другой пары поверхностей из первого и последующего семейств, расположенного по отношению к первому со смещением, определяемым завершением цикла формообразования, в результате которого произойдет первое замыкание образующей на номинальной поверхности.
Образование первой пары поверхностей резания должно соответствовать по времени циклу формообразования, в результате которого осуществляется первое и последующее касание кромок номинальной поверхности детали (в данном случае её образующей).
Данный цикл зададим:
a)
углом
, характеризующим равномерный поворот
режущей кромки инструмента от точки
касания с образующей обрабатываемой
поверхности детали по направлению В;
б) перемещениями в направлении равномерных поступательных движений: DX, DY, DZ за время поворота системы координат инструмента на угол ;
в)
углом поворота системы детали
по направлению равномерного вращательного
движения А
за то же время.
Пересечение поверхностей резания при формообразовании будем рассматривать на участке формирования образующей обработанной поверхности при контакте режущих кромок с номинальной поверхностью детали.
Поскольку
мы рассматриваем процесс формообразования,
осуществляемый при равномерном сложном
движении резания, и считаем, что формы
кромок одинаковы, постольку уравнение
i-ой
поверхности резания будет отличаться
от первой лишь разницей в суммарных
перемещениях системы инструмента в
направлении движения формообразования,
т.е. по подачам конечной величины, которая
будет задана циклом времени, определяющим
один полный оборот детали при:
на Z,
X
и Y.
Где
-
подача в
мм /об.
Будем
считать, что в начальных (подвижных)
системах координат инструмента, (которые
обозначим одинаково
, так как они
связаны с исходной системой координат
), задана неявным параметрическим
уравнением произвольная режущая кромка,
которая совершает сложное движение
резания так, что её контактная точка за
каждый цикл формообразования касается
номинальной поверхности детали или её
образующей.
При сложном движении резания параметры подач соответственно будут: для движения А - угол , движения DX, DY, DZ. Они являются функциями параметра движения резания и могут быть определены из соотношений:
,
,
(1.4)
,
.
где:
-
подача в мм на зуб (при фрезеровании);
-
число кромок (или число зубьев у фрезы);
-
передаточное отношение чисел оборотов
детали и инструмента.
Если
считать , что движение резания А и
движения формообразования В, DX
DY,
DZ
осуществляются последовательно, то
уравнение формообразующих поверхностей
резания можно записать как уравнения
поверхностей вращения от режущих кромок,
смещенных относительно друг друга в
исходной системе координат детали
.
На постоянные величины подач, за принятые
циклы формообразования, и определяемые
как константы
,
,
,
Оценим погрешность , которая будет заключаться в том, что точки режущей кромки и, в частности, контактная точка О вместо циклической линии опишет дугу окружности и, следовательно, произойдет искажение формы поверхности резания. Её можно оценить путем сравнения координат точки пересечения циклоид, касательных одной и той же линии поверхности и точки пересечения дуг окружностей при удалении точек касания на величину подачи на оборот точки.
Для этого запишем уравнения координаты Y точек пересечения дуг окружностей, удаленных на и циклоид, у которых также точки касания линии номинальной поверхности удалены на величину S о.
Для пересечения дуг окружностей:
;
(1.5)
Для пересечения циклоид:
(1.6)
Зависимость
(1.6) является трансцендентной. Осуществим
ее решение с помощью ЭВМ, используя
метод итерации. Для нескольких значений
подач
( мм./зуб.фр) и заданного радиуса фрезы
вычислим координату Y
по уравнениям (1.5)
и (1.6) и
определим порядок ошибки. Согласно
полученным данным очевидно, что
погрешность, связанная с заменой сложного
движения резания на простое при
последовательном формировании
поверхностей резания, может не учитываться,
так как её величина даже для грубой
обработки с подачей до
(мм/об.) не может быть зарегистрирована
современными приборами для оценки
шероховатости поверхности и составляет
0,4%.
Исходя из изложенных соображений, выведем уравнения поверхностей резания от первой и последующей режущих кромок как поверхностей первого семейства и уравнение поверхности резания последующего семейства, записывая уравнение движения кромки как твердого тела методом переноса начала и поворота осей временно подвижных систем координат и приводя запись уравнения к исходной системе координат .
Зададим все перемещения кривым режущих кромок согласно общей схеме формообразования (рис1.7) произвольной номинальной поверхности.
Для
этого определим промежуточные исходные
системы координат в зависимости от
начала и конца цикла совершаемых
движений. Выберем систему координат
инструмента -
. В данной системе координат за цикл от
касания первой режущей кромкой идеальной
поверхности до касания последующей
совершаются следующие перемещения.
Поворот системы координат
на угол
относительно центра системы: перемещение
начала этой системы в направлении
указанных движений DX,
DY,
DZ.
Для записи уравнения, связывающего
указанные движения первой кромки методом
поворота осей, исходной системой
координат будет система
.
Для последующей - поворот системы
координат
на угол
,
перемещение начала системы по стрелкам
соответственно: DX,
DY,
DZ.
Исходная
система координат
.
Запишем уравнения преобразования систем координат относительно исходной, определяющие уравнения двух траекторий:
Для первой
,
,
(1.7)
;
Для последующей
,
,
(1.8)
Перейдем к записи выражения (1.8) в исходной системе, приводя начальные системы координат сразу к общему виду:
(1.9)
тогда для последующей
(1.10)
Для регистрации оставшегося неучтенным перемещения перейдем к системе координат детали через следующие уравнения преобразований. Переход от системы к системе
,
,
(1.11)
.
Переход от системы к системе :
,
,
( I.12)
.
Переход
от системы
к исходной системе детали
представим
в виде
(1.13)
Чтобы
записать конечные уравнения, отметим,
что уравнения преобразования,
регистрирующие относительный поворот
системы координат детали, аналогичны
уравнениям (1.7) и (1.8) причем: для фиксирования
перемещения первой режущей кромки -
исходной системой координат будет
,для
последующей - исходной системой координат
будет
.
В
уравнении , в отличии от уравнений (1.7)
и (1.8) , приращения
равны нулю, а угол
заменит угол
,
равный
.
Итак, уравнение, связывающее относительный поворот системы координат детали, для записи уравнения движения первой линии режущей кромки будет (см. рис.1.7).
,
(1.14)
(где - начальная система координат).
Аналогичное уравнение для траектории движения, совершаемой второй режущей кромки будет:
(1.15)
(где
- начальная система координат).
Так как для записи уравнений поверхностей в одной системе координат следует перейти от системы к системе координат , то значение координат из соотношения (1.15) следует подставить в соотношение (1.14).
или
(1.16)
Принимая
систему
из уравнения (1.3) за начальную (т.е.
для уравнений (1.4) и (1.16)), запишем уравнения
поверхностей резания в единой системе
координат детали
как уравнения, определяющие существование
семейств траекторий резания от точек
режущей кромки, движение которых
подчинено общему закону. Для этого в
начальный момент формообразования
(т.е. в исходной системе координат
инструмента
) зададим линию кромки неявными функциями
связи параметра, определяющего положение
точек на линии кромки, с координатами
.
(1.17)
Тогда уравнение поверхности резания от первой режущей кромки, от последующей и уравнение поверхности резания от режущей кромки образующей новое семейство поверхностей резания будет отличаться от предшествующего уравнения лишь включенными величинами, определяющими перемещения вдоль указанных векторов за время полного оборота детали, и будет:
(1.18)
Общее уравнение поверхностей резания полученное ранее, может быть представлено упрощенной последовательной записью систем параметрических уравнений.
,
(1.17)
где: P- перометор определяющий перемещение точки по линии
(1.19)
,
,
(1.20)
.
где
- пространственные углы относительно
положения системы
и
в начальный период обработки.
(1.21)
Таким образом, по уравнению (1.21) можно рассчитать координаты ( ) точек поверхности или семейства поверхностей резания, относящиеся к исходной пространственной системе детали, в которой определенным образом ориентирована деталь и задана геометрически произвольная, формируемая поверхность [67].
I.4 Принципы получения многообразия кинематических вариантов формообразования задаваемых поверхностей выбираемой линией предполагаемого инструмента и сравнение их кинематической производительности на ЭВМ
При расчете координат точек поверхностей резания на ЭВМ очевидна возможность определения множества точек, принадлежащих формируемой поверхности детали, простой проверкой условия удовлетворения рассчитываемых координат алгебраическому или натуральному уравнению поверхности детали, заданной произвольно в той же системе. Выполнение этого условия дважды будет означать двукратное касание режущей кромки теоретически заданной, формируемой поверхности детали. Так как движение кромки осуществляется от исходного контактного положения по траектории резания, то двойное выполнение упомянутого условия за полный цикл формообразования определит возможный способ механической обработки. Количество кинематических вариантов формообразования заданной поверхности выбранной линией режущей кромки предполагаемого инструмента будет зависеть от следующих факторов:
a)
исходного положения систем координат
детали и инструмента в начале цикла
формообразования , характеризуемого
контактом линии кромки с поверхностью
детали в точке О, задаваемого выбором
углов
(при расчете шести оставшихся углов по
уравнениям связи их косинусов);
б)
сочетания действующих движений из числа
существующих
,
определяющего результирующее движение
резания, составляемое из попеременного
включения пяти элементарных движений
для каждого случая. При этом численная
оценка множества общих точек поверхностей
резания и детали, выполняемая за заданный,
расчетный временной цикл формообразования
будет определять производительность
способа механической обработки. Выбор
способа механической обработки и
следовательно его производительность
уже будет зависеть от комбинации,
определяемых пунктами a)
и б).
в)
существования
и величины радиуса движения режущей
кромки относительно центра си системы
координат, предполагаемого инструмента
;
заданного выбираемой линией режущей
кромки.
г)
выбора главного движения резания,
определяющего скорость резания
,
из числа существующих в комбинациях,
определяемых пунктами а), б), в) при
присвоении оставшимся, существующим
движениям функции подач;
д)
возможности увеличения скорости
выбранного движения резания при
многолезвийной обработке, соответствующей
условию
,
определяющему фрезерование, при котором
многолезвийная обработка характеризуется
приближенно равной мощности резания с
однолезвийной, т.е. одновременный контакт
нескольких формообразующих режущих
кромок с обрабатываемой поверхностью
исключен; (сравнение производительности
формообразования способов механической
обработки, имеющих разную мощность при
выполнении функций резания и
формообразования, исключается);
е) возможности отыскания способа обработки при выборе соотношений и направлений движений, принятых как подача или выборе скоростного движения резания как сложного, составного из нескольких элементарных движений при изменении направления движения;
ж)
выбора величин параметров формы линии
режущей кромки, (например, шага - Н, или
угла подъема винтовой линии -
при заданном радиусе -
,
определяемых параметром винтовой линии
- Р).
Выше изложенные условия определяют поисковый алгоритм с оценкой производительности принципиально-возможных способов формообразования заданной поверхности предполагаемым инструментом, который был разработан и реализован на языке Паскаль 4 на ЭВМ ЕС [42], для различных поверхностей деталей. Согласно изложенной методике алгоритм предусматривал расчет производительности определяемых способов формообразования по упрощенной формуле Дикушина А.И.
,
где
-
время цикла формообразования ;
рассчитывалось по формулам:
.
Шаг дискретного движения режущей кромки от скорости резания принимался равным:
при
при
где
- принятое произвольно число режущих кромок возможной фрезы.
Шаг дискретного движения кромки в направлениях возможных подач принимался постоянным и равным:
где
,
принятое значение подачи при получистовой
обработке. Это обеспечивало шаговое
равенство расположения контактных
точек (КТ) на формируемой поверхности
при сравнении различных способов
обработки из принципиально-возможных,
что позволяло сравнить однотипные
операции, обеспечивающие одинаковую
технологическую шероховатость
поверхности.
Печать алгоритма предусматривает выход характеристик способа механической обработки для трех наиболее эффективных из принципиально возможных, сравниваемых по производительности.
Пример расчетного анализа на ЭВМ способов формообразования наружных поверхностей вращения деталей типа валов показал:
в случае формообразования точкой (из условия выбора кромки, как участка пересечения двух прямых линий, или существования малого радиуса R и) , наиболее эффективны три способа (рис.1.8) а), б), с);
в случае формообразования прямой линией способы повторяются:
для случая а) ПР=45000 (КТ)
для случая б) ПР=10000 (КТ)
для случая с) Пр=450000 (КТ)
в случае формообразования винтовой линией с углом подъема W=
на радиусе фрезы
, получено три способа обработки на
базе
схемы - в);
а) оси фрезы и детали параллельны = 10000 (КТ)
в) находятся под углом скрещивания = 10000 (КТ)
с) находятся под углом скрещивания и фреза имеет ещё подачу вдоль своего вращения = 450000 (КТ).
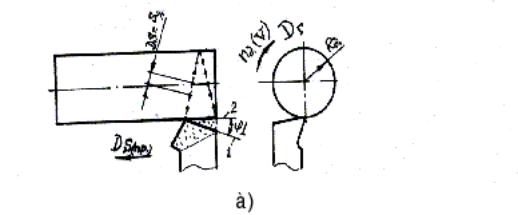
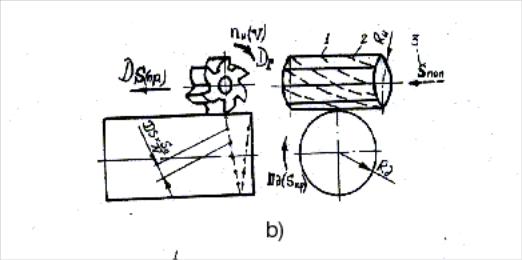
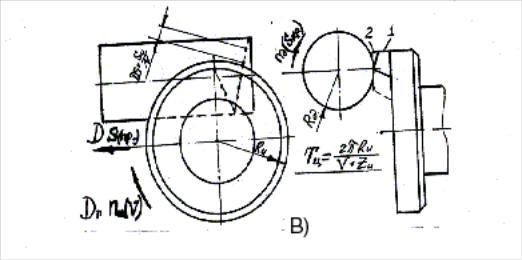
Рис.1.8
Таким образом, метод и алгоритм позволяют системно решить такую сложную задачу, как определение наиболее эффективных способов механической обработки из числа принципиально-возможных.
Алгоритм существенно облегчает работу в области повышения эффективности операций механической обработки, позволяет решить эту задачу на уровне изобретений [37].
Так схема обработки, изображенная на рис.с защищена была авторским правом ещё в 1946 г. Схема B(1) составила предмет изобретения , а схемы B(2) и B(3) разработаны и защищены авторскими свидетельствами при реализации описанного алгоритма на ЭВМ. Схема представленная на рис.a) известна как самая эффективная при формообразовании точкой.
Ниже
приведена блок схема алгоритма поиска
наиболее производительных схем
формообразования задаваемых уравнением
поверхностей деталей
да
нет
нет
да
нет
да
да
нет
нет
да
нет
да
нет
нет
да
да
JJ=JJ+1
нет
I=I+1
да
да
нет
нет
да
нет
да
нет
да
ПR(JJ)=КТ/Т
нет
да
да
да
нет
да
нет
ПR(3)=ПR(JJ)
нет
ПR(1)=ПR(JJ)
да
нет
ПR(2)=ПR(JJ)
Ранее нами был рассмотрен поисковый алгоритм определения схем формообразования заданных поверхностей и выбора трех наиболее производительных, (с позиции кинематики формообразования), из принципиально (или теоретически) возможных. Алгоритм после сравнения схем формообразования и определения наиболее производительных предусматривает печать:
углов относительно положения систем координат детали и инструмента в соответствии с общей кинематической схемой формообразования, определяющих относительное положение предполагаемого инструмента в исходный момент формообразования;
форму режущей кромки инструмента при выборе на печать значений
(т.е. если это ломаная линия, расположенная
от центра
на расстояния R
, то или
в зависимости от исходного задания
параметрического уравнения режущей
кромки в системе инструмента
).
(Второй пример:
,
следовательно режущая кромка винтовая
линия на цилиндре или поверхности
вращения с осью вращения соответствующей
и т.д.)равенство (неравенство) радиуса или другого параметра инструмента, определяющего положение режущей кромки в системе
и
нулю.наличие движений, необходимых для формообразования, т.е. неравенство нулю сочетаемых их всех от одного до 6 движений: А, В, DX, DY и DZ, которое задается непрерывным вращением одного из заданных пространственных углов
,
определяющих как относительное положение
систем детали
и инструмента
в исходный момент формообразования,
так и вращение промежуточной , несущей
системы
вокруг любой из трех осей координат;печать главного движения резания из существующих для найденной, наиболее эффективной схемы формообразования, например:
и т.д.
После получения данной информации на печать ПЭВМ можно изображать полученную схему формообразования. По примеру графического исполнения кинематических схем резания, приведенного в работе Грановского Г.И. Только с изображением формируемой поверхности в системе координат детали в положении, определяемым ее алгебраическим уравнением. И линии режущей кромки инструмента, положение которой в системе координат инструмента задано параметрическим уравнением.