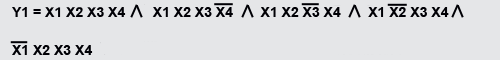1. Основные понятия, элементы и формы Булевой алгебры
Основные понятия Булевой алгебры.
Логическая переменная – это переменная, которая может принимать одно из двух значений ноль и единица (истина или ложь). Логическая константа – это константа (постоянная величина) которая может принимать значение ноль или единица (истина или ложь). Логическая функция – это функция, которая может принимать два значения ноль и единица (истина или ложь).
Наиболее универсальным средством представления логической функций может являться таблица истинности.
Таблица истинности – это таблица, показывающая все входные и выходные значения высказывания, процесса, действий и т.д. Приведем простой пример:
Ребенку очень хочется пойти погулять на улицу. У него есть папа, мама, бабушка и дедушка. Что бы ему разрешили идти гулять необходимо согласие хотя бы двух взрослых. Таким образом, согласие взрослого выразим цифрой “1”, не согласие “0” и построим таблицу истинности.
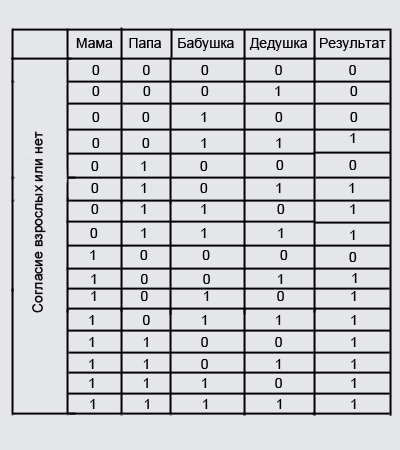
Глядя на таблицу истинности видны все варианты исхода событий. Значение результата, где он равен “1” означает, что ребенок пойдет гулять, “0” — не пойдет.
А вот так выглядят таблицы истинности для основных (двоичных) функций.
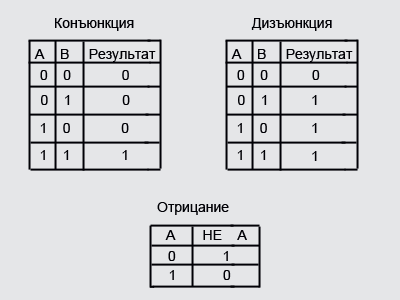
Наиболее широкое применение в алгебре логики получила функционально полная система функций (Булевый базис), выраженная в виде базовых логических функций одной переменной “ НЕ ” (отрицание) и двух функций двух переменных – это “И” (конъюнкция или логическое умножение) и “ИЛИ” (дизъюнкция или логическое сложение).
Основные элементы Булевой алгебры.
В Булевой алгебре логические выражения включают такие логические операции, как “И”, “ИЛИ” и “НЕ” могут быть представлены в виде различных сочетаний. Для получения результата должна быть определенная последовательность действий. И представлена она вот таким видом:
1. Рассчитываются значения отрицаний и скобок; 2. Выполняется операция логического умножения (“И”); 3. Выполняется логическое суммирование (“ИЛИ”)
Для работы с логическими выражениями используются некоторые законы и правила:
Формы представления логических функций в Булевой алгебре.
Для выражения логических функций особое место занимают две канонические формы – это: 1. Совершенная дизъюнктивная нормальная форма (СДНФ); 2. Совершенная конъюнктивная нормальная форма (СКНФ).
СДНФ – это дизъюнкция простых конъюнкций, отражающая наборы переменных, где функция имеет единичные значения. Эти значения называются конституенты единицы.
СДНФ функции f содержит ровно столько конъюнкций, сколько единиц в таблице истинности f ; каждому единичному набору (x1, x2, ..., xn) соответствует конъюнкция всех переменных, в которой xi взято с отрицанием, если xi = 0, и без отрицания, если xi = l.
Рассмотрим это на нашем простом примере (описанном выше) про ребенка.
Для удобства приравняем Мама = X1; Папа = X2; Бабушка = X3; Дедушка = X4, а результат = Y1.
Суммируем (дизъюнкция) произведения (конъюнкция) всех наборов Х1 X2 X3 X4, где Y1 = 1, причем если Xi = 0, то обозначается как «не X», а если Xi = 1, то просто X. Вот что получаем.
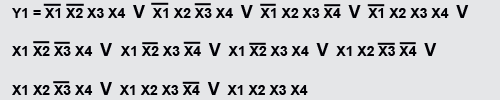
СКНФ – это конъюнкция простых дизъюнкций, отражающая наборы переменных, где функция имеет нулевые значения. Эти значения называются конституенты нуля. Возьмем во внимание предыдущий пример с такими же исходными данными и найдем для него СКНФ.
Перемножим (конъюнкция) суммы (дизъюнкция) всех наборов Х1 X2 X3 X4, где Y1 = 0, причем если Xi = 0, то обозначается X, а если Xi = 1, то “ не X ”, (т.е СКНФ своего рода противоположность от СДНФ). Вот что получаем.
