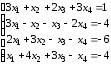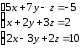ИПР№1_Excel
.docxМинистерство образования Республики Беларусь
Учреждение образования
«Белорусский государственный университет информатики и радиоэлектроники»
Факультет инновационного непрерывного образования
Кафедра экономической информатики
«К защите допустить»
_____________О.М.Раптунович
__.___.2018
ИНДИВИДУАЛЬНАЯ ПРАКТИЧЕСКАЯ РАБОТА №1
по дисциплине
«Прикладные системы обработки данных»
Выполнил: студент группы 792351
Быкович Екатерина Ивановна
Подпись студента________________
Дата____________________________
2018
Задание 1. Построить в MS Excel графики функции в соответствии с заданным вариантом.
Задание 1.1. Вычислить значения функции в заданном диапазоне в соответствии с вариантом. Аргумент и значение функции выводить в таблице с 3 знаками после запятой. На основании табличных данных, построить график функции на заданном диапазоне (тип диаграммы – точечная).
|
№ вар. |
|
Диапазон |
|
1 |
|
900.. 1800 |
Для построения графика данной функции необходимо знать, что значения x нужно представить в радианах, тангенс угла в 900 не определен, тангенс угла в 1800 равен нулю, косинус угла в 900 равен нулю, косинус угла в 1800 равен минус 1. Таким образом функция принимает значение ноль в точке 900 и значение минус один в точке 1800.
Переходим к построению графика. Введем значение х в градусах с шагом 5 градусов. Используем команду Заполнить – Прогрессия. После ее выполнения появится диалоговое окно Прогрессия, которое заполним следующим образом: в группе Расположение установим переключатель в положение По столбцам; в группе Тип выберем Арифметическая; в поле Шаг введем значение выбранного нами шага, т.е. введем 5; в поле Предельное значение установим 180; выполняем команду ОК. Далее переведем градусы в радианы по формуле =РАДИАНЫ().
В ячейки С5 и С23 вносим значения 0 и минус 1 соответственно. В ячейку С6 вносим формулу: =(TAN(B6))/3+COS(B6), и протягиваем ее до предельного значения х.
Выделяем диапазон ячеек В5:С23, далее Вставка – Диаграммы – Вставить график – Точечная.
Результат выполнения задания представлен на рисунке 1.
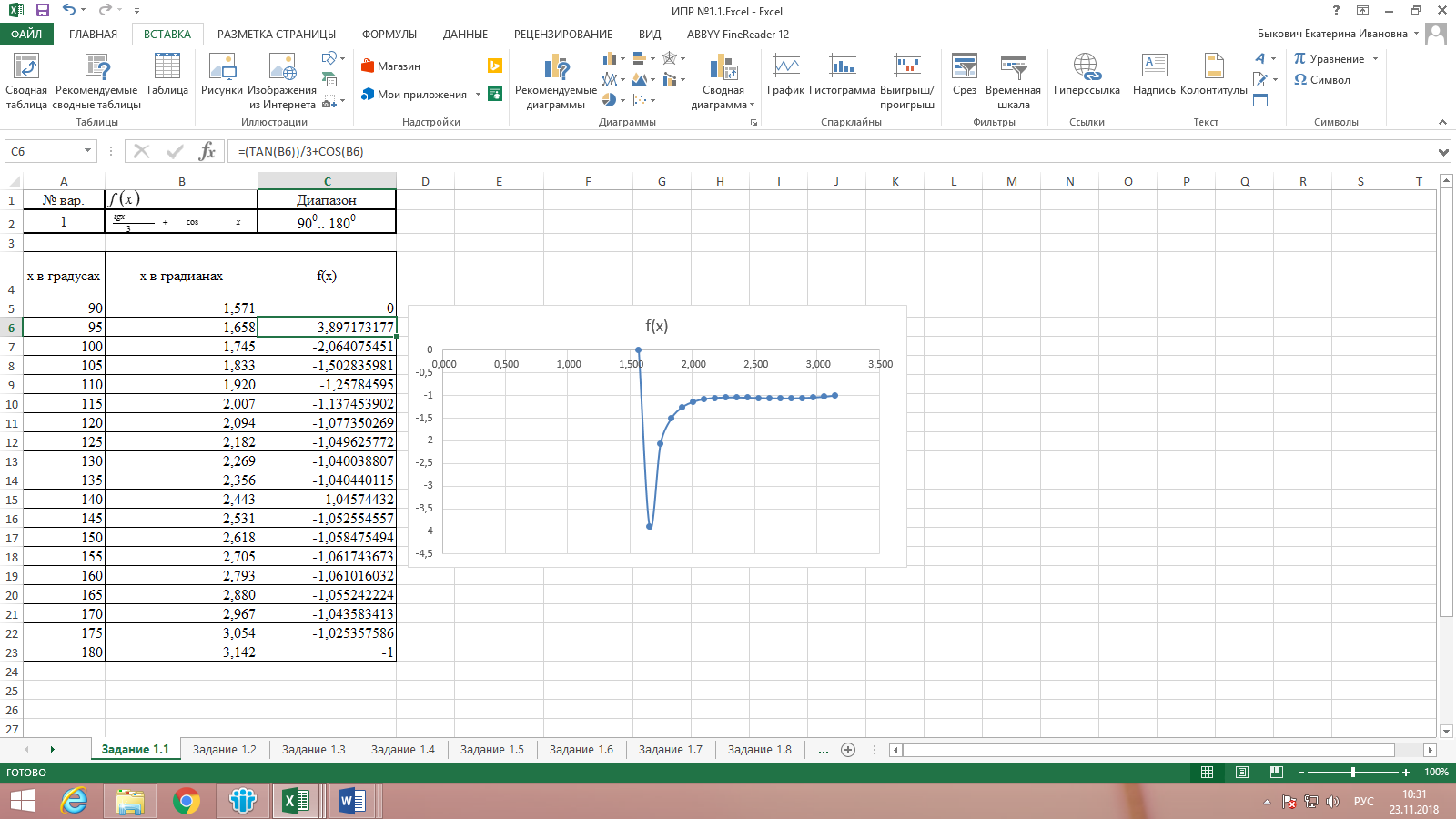
Рисунок 1. Результат выполнения задания 1.1
Задание 1.2. Построить в одной системе координат графики следующих двух функций.
|
№ вар. |
|
Диапазон |
|
1 |
|
|
Для построения графиков функций y, z в одной системе координат выполняем следующие действия:
-
Заполняем значение х в соответствии с диапазоном от минус 1,6 до 2,2. Зафиксируем значение минус 1,6 в ячейке А6, вызываем команду Заполнить – Прогрессия. После ее выполнения появится диалоговое окно Прогрессия, которое заполним следующим образом: в группе Расположение установим переключатель в положение По столбцам; в группе Тип выберем Арифметическая; в поле Шаг введем значение выбранного нами шага, т.е. введем 0,2; в поле Предельное значение установим 2,2; выполняем команду ОК.
-
В ячейку В5 вставим формулу в соответствии с функцией y: =2*SIN(2*ПИ()*A6)*COS(ПИ()*A6)+SIN(3*ПИ()*A6). И протянем формулу вниз до предельного значения x.
-
В ячейку С6 вставим формулу функции z: =COS(2*ПИ()*A6)*SIN(ПИ()*A6)^2-COS(4*ПИ()*A6). И протянем формулу вниз до предельного значения x.
-
Выделяем диапазон В6:С25, далее Вставка – Диаграммы – Вставить график – График с маркерами. Корректируем наименование графика и значения рядов.
Результат выполнения задания представлен на рисунке 2.
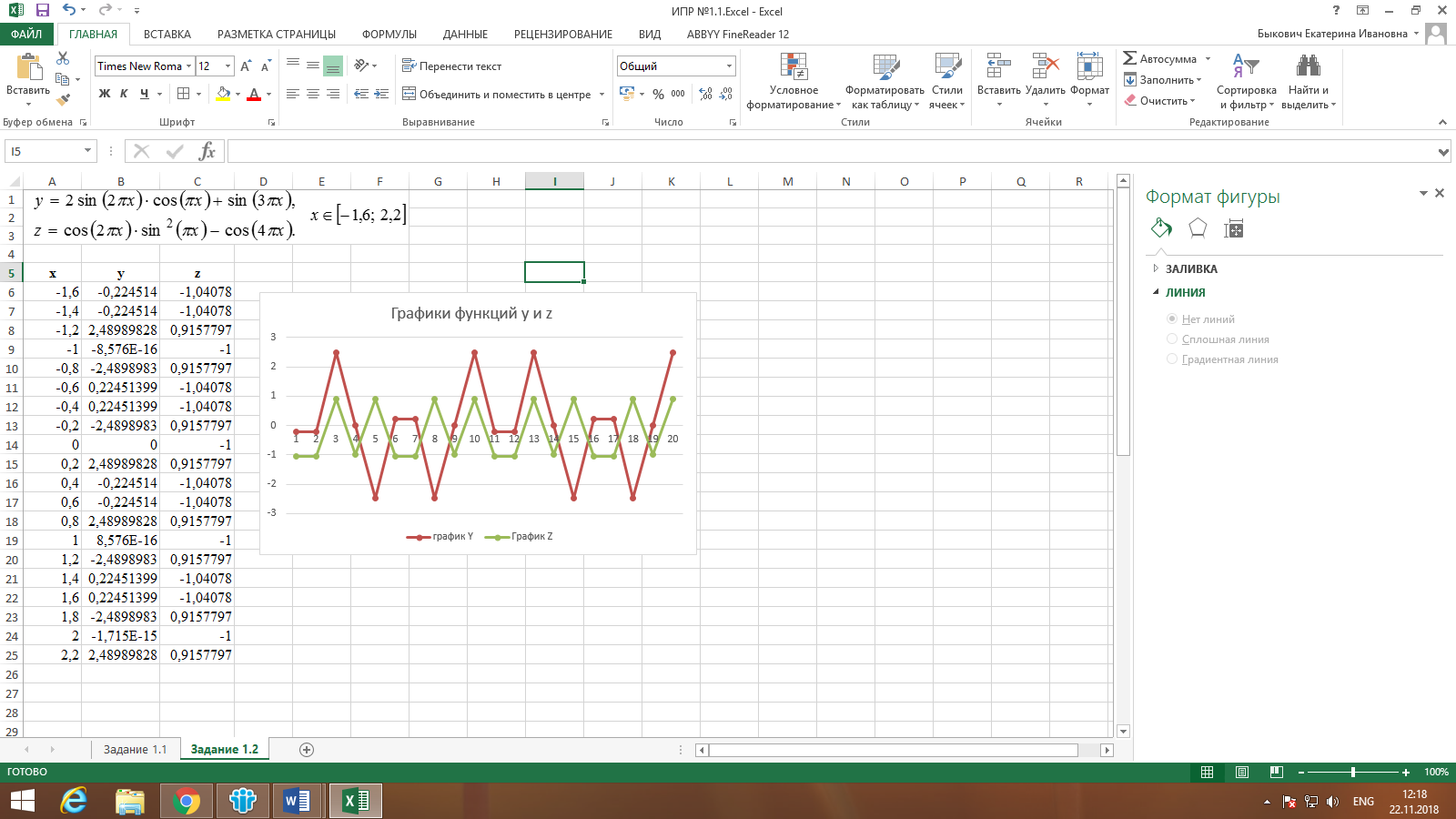
Рисунок 2. Результат выполнения задания 1.2
Задание 1.3. Построить в разных системах координат графики следующих функций.
|
№ вар. |
|
Диапазон |
|
1 |
|
|
Построим график функции Y.
Заполняем значение х в соответствии с диапазоном от минус 2 до 2. Зафиксируем значение минус 2 в ячейке А19, вызываем команду Заполнить – Прогрессия. После ее выполнения появится диалоговое окно Прогрессия, которое заполним следующим образом: в группе Расположение установим переключатель в положение По столбцам; в группе Тип выберем Арифметическая; в поле Шаг введем значение выбранного нами шага, т.е. введем 0,1; в поле Предельное значение установим 2; выполняем команду ОК.
В ячейку В19 вставляем формулу соответственно функции Y: =(1+A19^2)/(1+2*A19^2). Протягиваем формулу до предельного значения х.
Выделяем диапазон А19:В59, далее Вставка – Диаграммы – Вставить график – График с маркерами. Корректируем наименование графика (рис. 3).
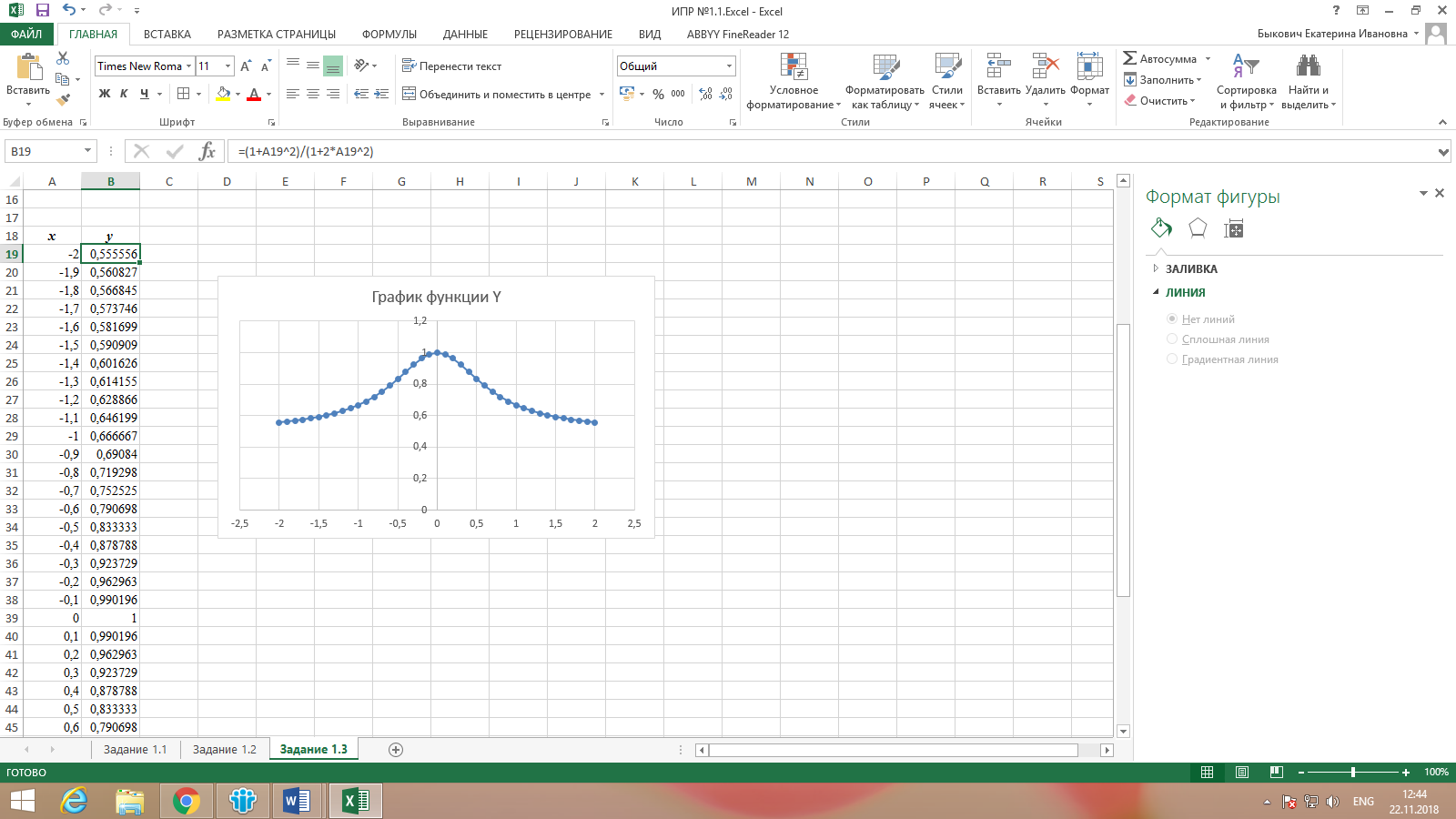
Рисунок 3. Результат выполнения задания 1.3 (Y)
Построим график функции G.
Заполняем значение х в соответствии с диапазоном от минус 2 до 2. Зафиксируем значение минус 2 в ячейке L19, вызываем команду Заполнить – Прогрессия. После ее выполнения появится диалоговое окно Прогрессия, которое заполним следующим образом: в группе Расположение установим переключатель в положение По столбцам; в группе Тип выберем Арифметическая; в поле Шаг введем значение выбранного нами шага, т.е. введем 0,1; в поле Предельное значение установим 2; выполняем команду ОК.
В ячейку М20 вставляем формулу в соответствии функции G: =ЕСЛИ(L20<=0;3*SIN(L20)-COS(L20)^2; ЕСЛИ(L20>0;3*КОРЕНЬ(1+L20^2))). Протягиваем формулу до предельного значения х.
Выделяем диапазон L19:M59, далее Вставка – Диаграммы – Вставить график – График с маркерами. Корректируем наименование графика (рис. 4).
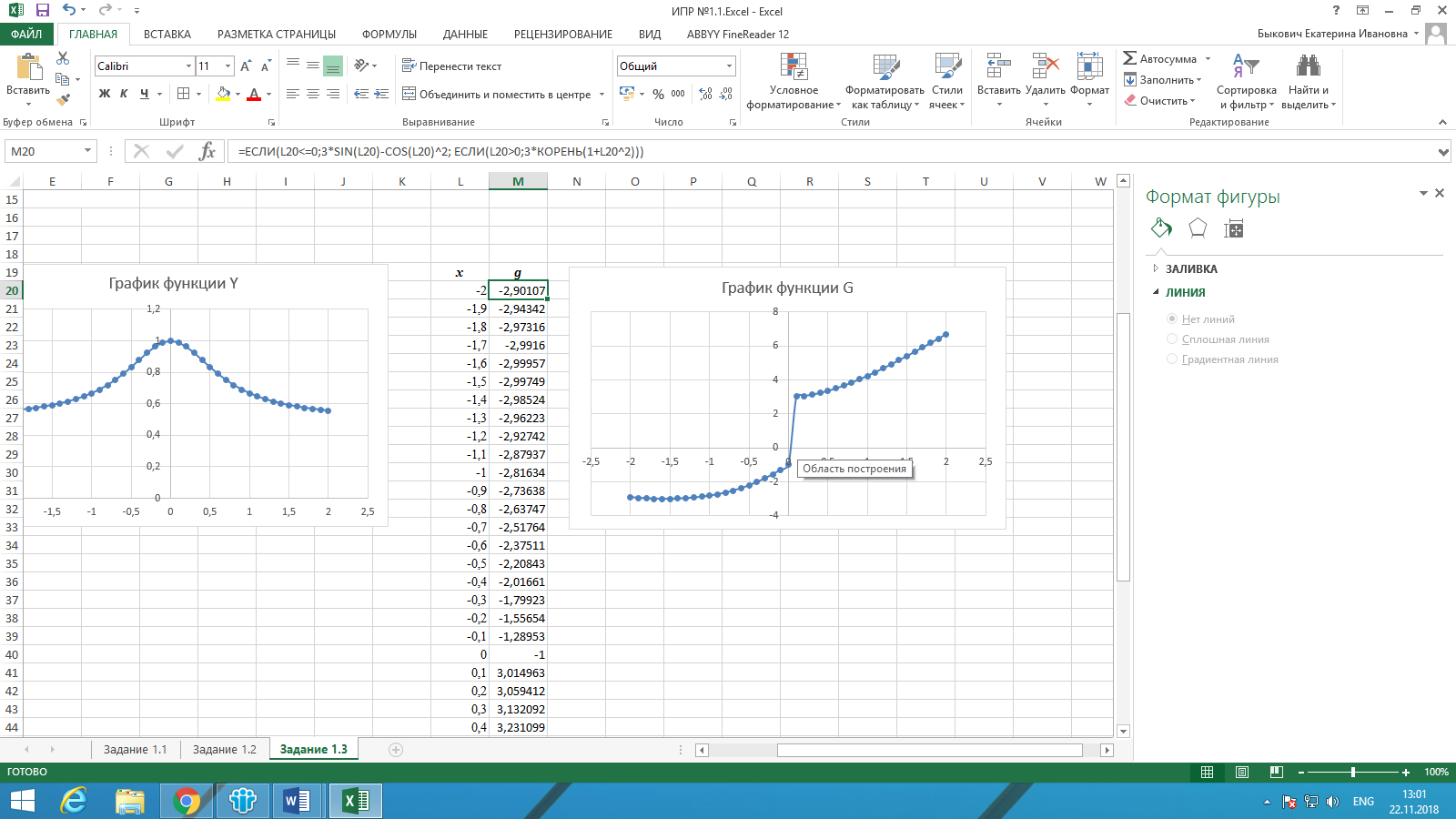
Рисунок 4. Результат выполнения задания 1.3 (G)
Построим график функции Z.
Копируем значения х.
В ячейку В63 вставляем формулу в соответствии с функцией Z: =ЕСЛИ(A63<=0;(1+A63)/(1+A63^2)^1/3; ЕСЛИ(И(A63>=0;A63<=1);-A63+2*EXP(-2*A63);ABS(2-A63)^1/3)). И протягиваем до предельного значения х.
Выделяем диапазон A63:B103, далее Вставка – Диаграммы – Вставить график – График с маркерами. Корректируем наименование графика (рис. 5).
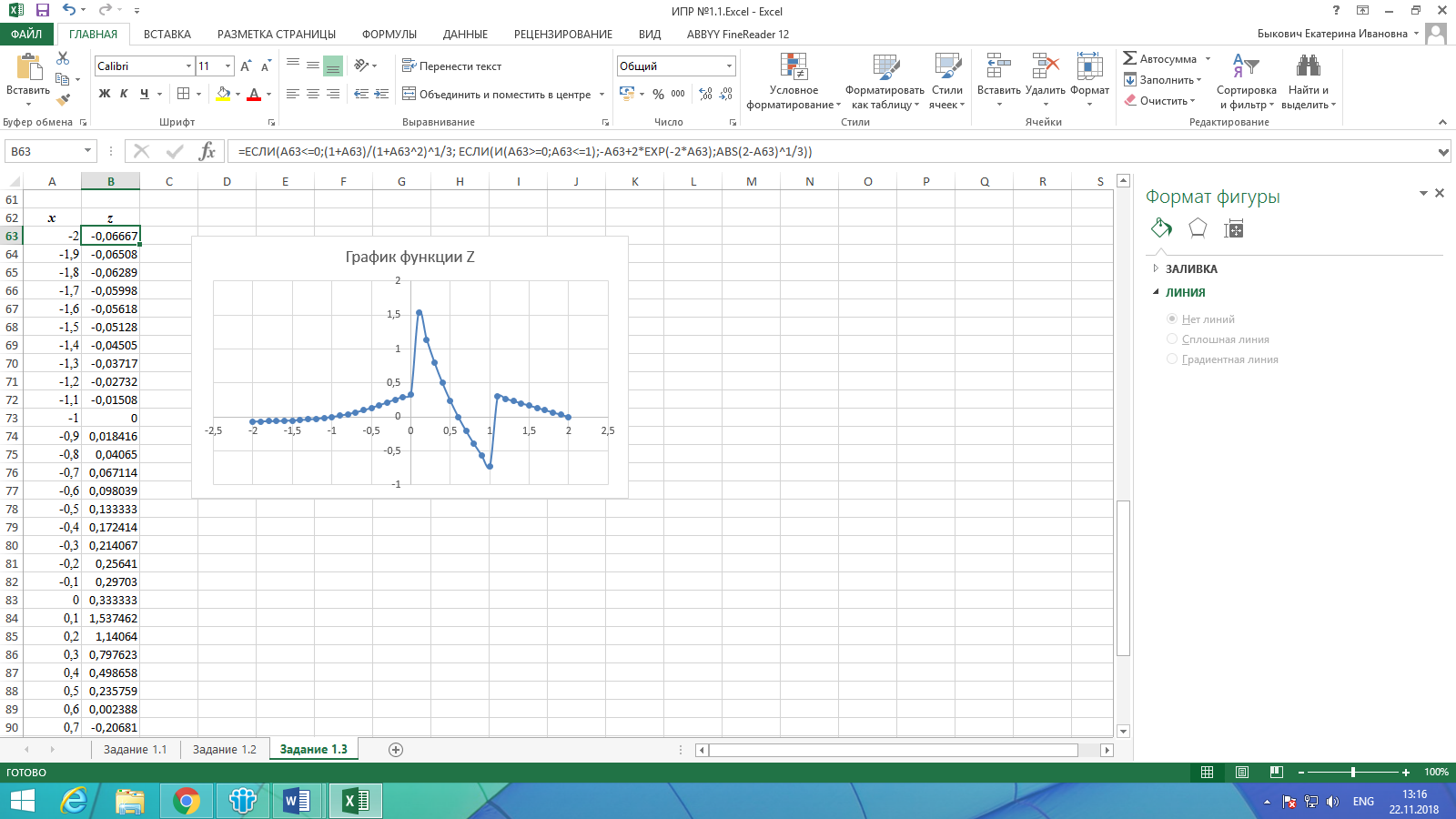
Рисунок 5. Результат выполнения задания 1.3 (Z)
Вариант
1.4.
Используя команду Подбор параметра из
меню Сервис, найти значение Х, при котором
функция
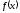 возвратит заданное значение.
возвратит заданное значение.
|
№ вар. |
Переменная |
|
Результат |
||
|
X |
Y |
Z |
|||
|
1 |
|
4,25 |
3,04 |
|
9,82 |
Создадим таблицу следующего вида. В ячейке F3 вставим формулу соответственно функции f(x): =B3^2+КОРЕНЬ(C3+LN(D3)). В итоге получается значение 2,31557. Оставаясь в этой же ячейке, вызываем команду Данные – Анализ «что, если» - Подбор параметра – заполняем окно как показано на рис. 7.
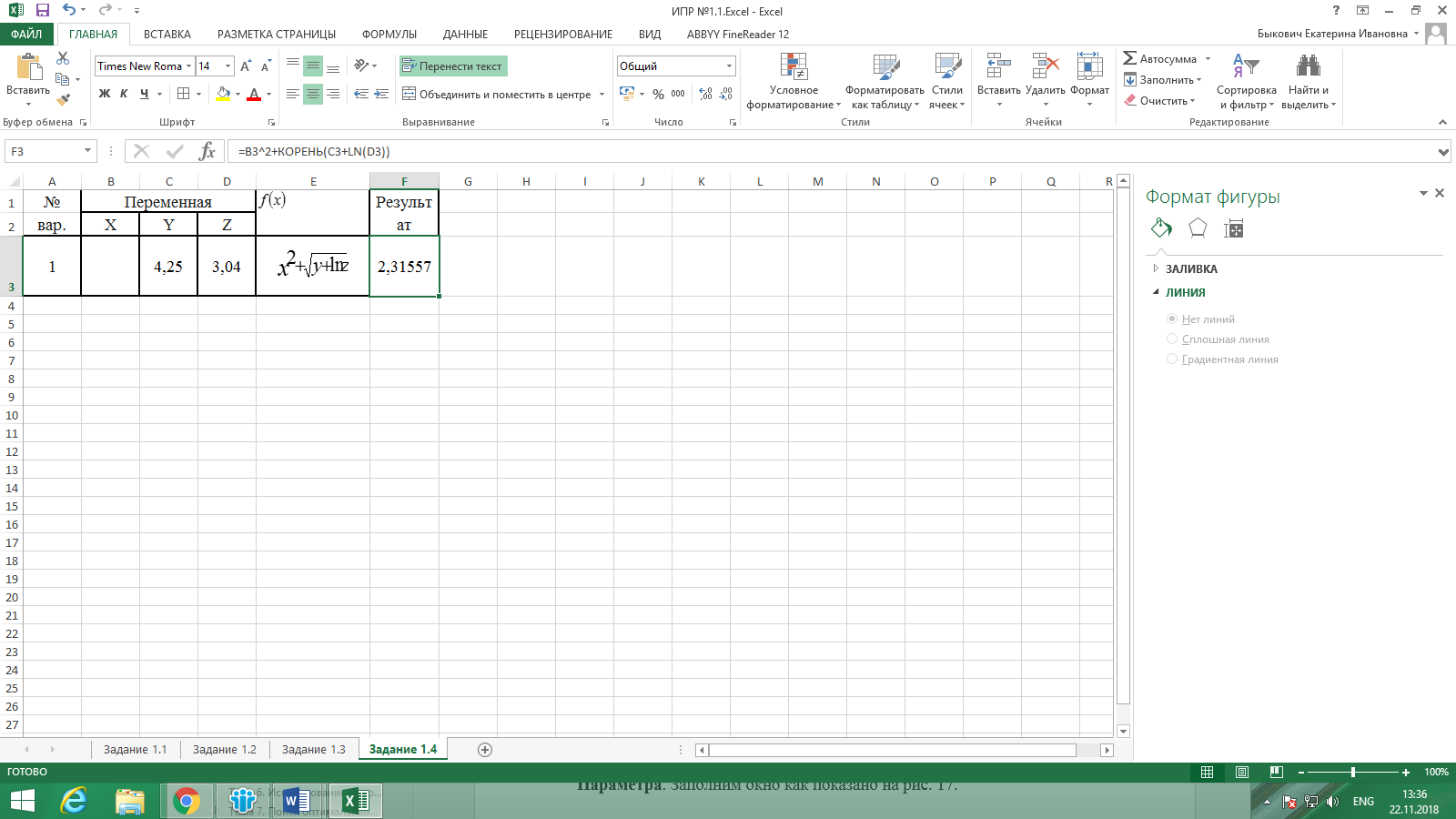
Рисунок 6. Заполнение формы задания 1.4
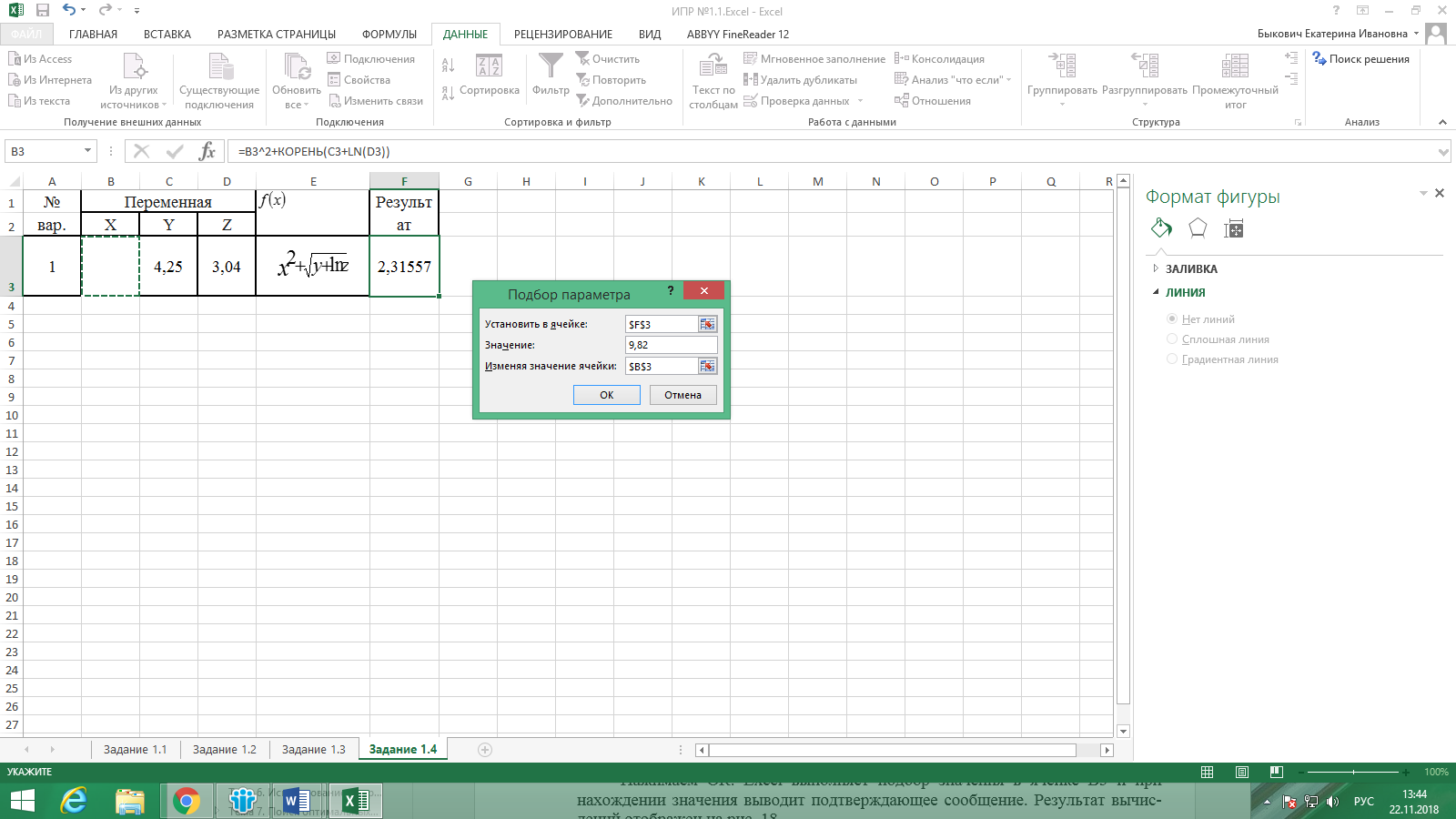
Рисунок 7. Заполнение окна Подбора параметров
Нажимаем ОК. Excel выполняет подбор значения в ячейке B3 и при нахождении значения выводит подтверждающее сообщение. Результат вычислений отображен на рис. 8.

Рисунок 8. Результат выполнения задания 1.4
Вариант
1.5.
Построить график функции
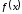 .
.
|
№ вар. |
|
|
1 |
|
Определим функцию. Для этого необходимо выбрать диапазон, в котором будет построен график. Пусть, например, от -3 до 3, шаг автозаполнения будет равен 0,2. В ячейку В6 вставим формулу: =((2+A6)^2*(A6)^2-1)^1/3.
Выполнив все необходимые действия по построению графика, получим результат, который представлен на рис. 9.
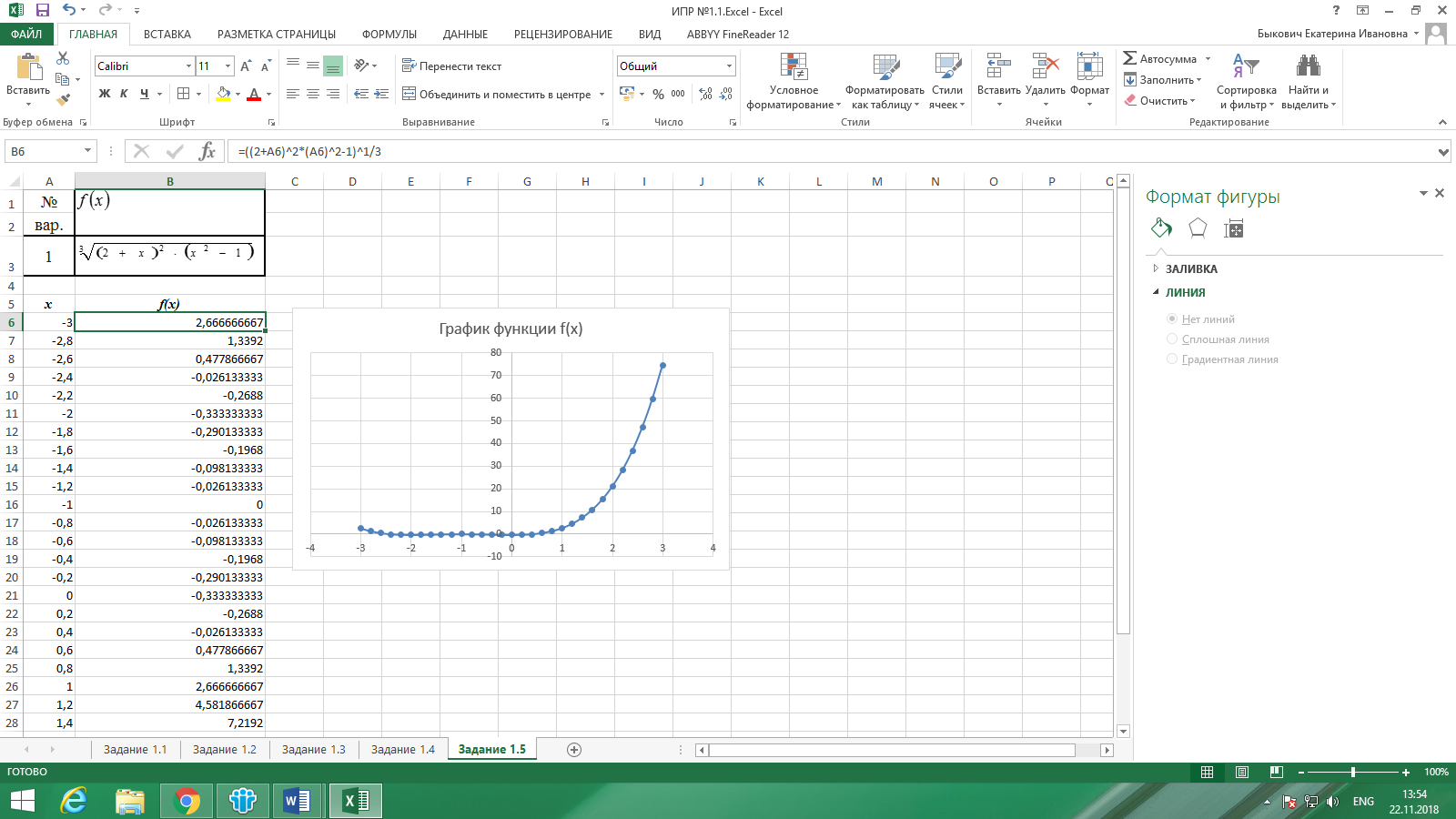
Рисунок 9. Результат выполнения задания 1.5
Вариант
1.6 Построить
график функции
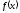 .
.
|
№ вар. |
|
|
1 |
|
При
построении этого графика следует
обратить внимание на область определения
функции. В данном случае функция не
существует при обращении знаменателя
в ноль. В этом случае 2,5х+7≠0,
х≠ -2,8. Из
этого следует, что
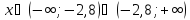 .
.
Определим значение аргумента в два этапа: например, от -5 до 3 с шагом 0,2. При построении графика необходимо помнить, что х≠ -2,8.
Выполнив все необходимые действия по построению графика, получим результат, который представлен на рис. 10.

Рисунок 10. Результат выполнения задания 1.6
Вариант
1.7.
Построить график функции
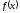 .
.
|
№ вар. |
|
|
1 |
|
Выполнение задания и построение графика производится аналогично заданию 1.3.
Значение х возьмем от минус 3 до 3 с шагом 0,2. Будем использовать функцию ЕСЛИ. В ячейку В6 вставляем формулу: =ЕСЛИ(A6<=0;(1+A6^2)/КОРЕНЬ(1+A6^4);2*A6+SIN(A6)^2/(2+A6)).
Выполнив все необходимые действия по построению графика, получим результат, который представлен на рис. 11.
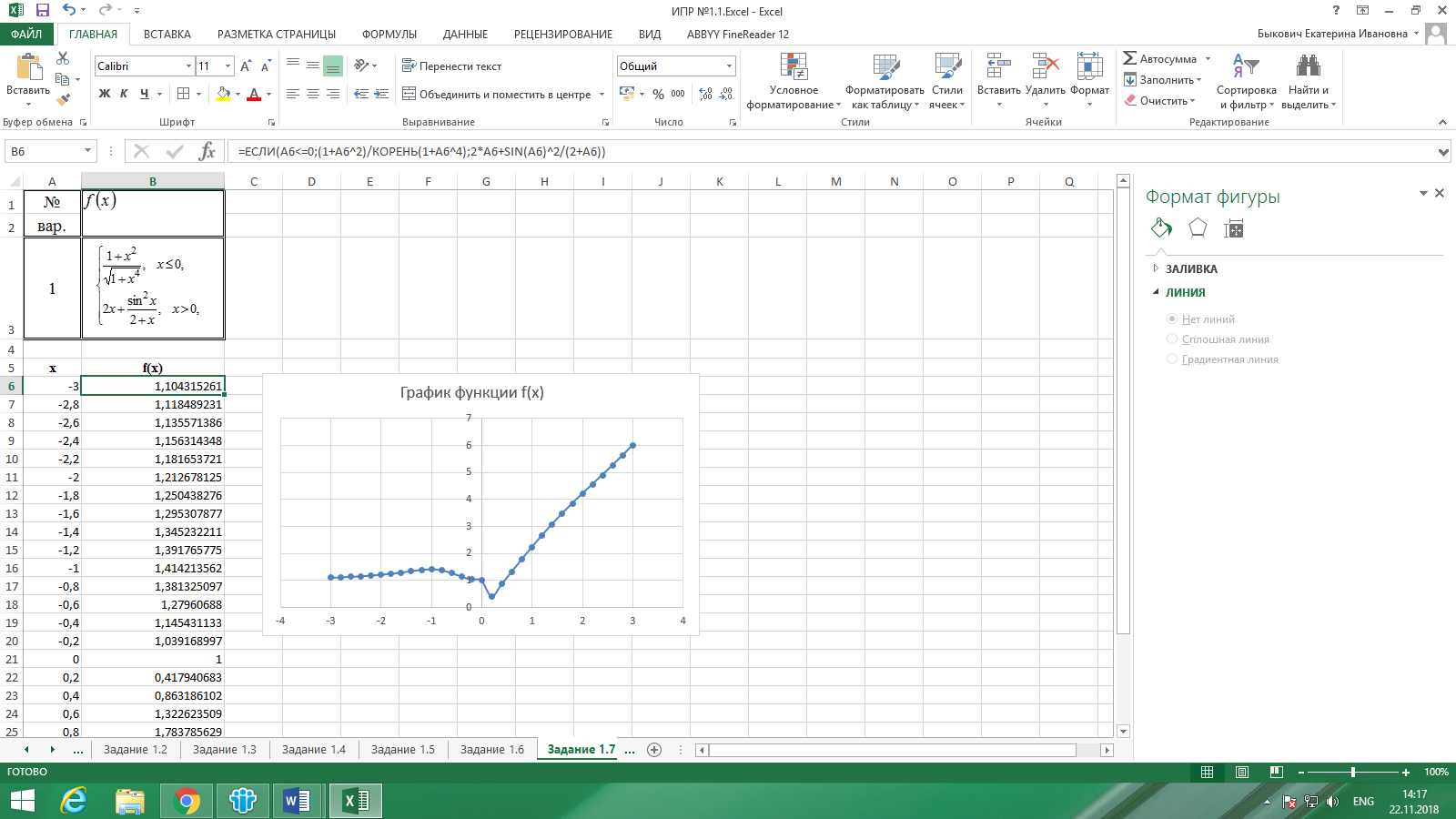
Рисунок 11. Результат выполнения задания 1.7
Вариант
1.8. Изобразите
линии заданные неявно уравнением
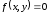
|
№ вар. |
|
|
1 |
|
Поскольку линия задана неявно, то для ее построения необходимо разрешить заданное уравнение относительно переменной y:
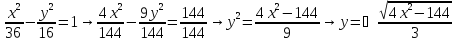
После
выполнения необходимых преобразований
можно увидеть, что линию
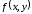 можно изобразить, построив графики двух
функций в одной графической области.
можно изобразить, построив графики двух
функций в одной графической области.
f1(x)=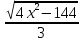
f2(x)=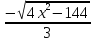
Перед
построением определим ОДЗ функций
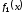 и
и
 .
.
Данные функции содержат в числителе выражение под знаком квадратного корня, поэтому обязательным условием их существования будет выполнение следующего неравенства:

Перейдем к построению графика. Введем значение х в диапазоне от минус 10 до минус 6, от 6 до 10, с шагом 0,2.
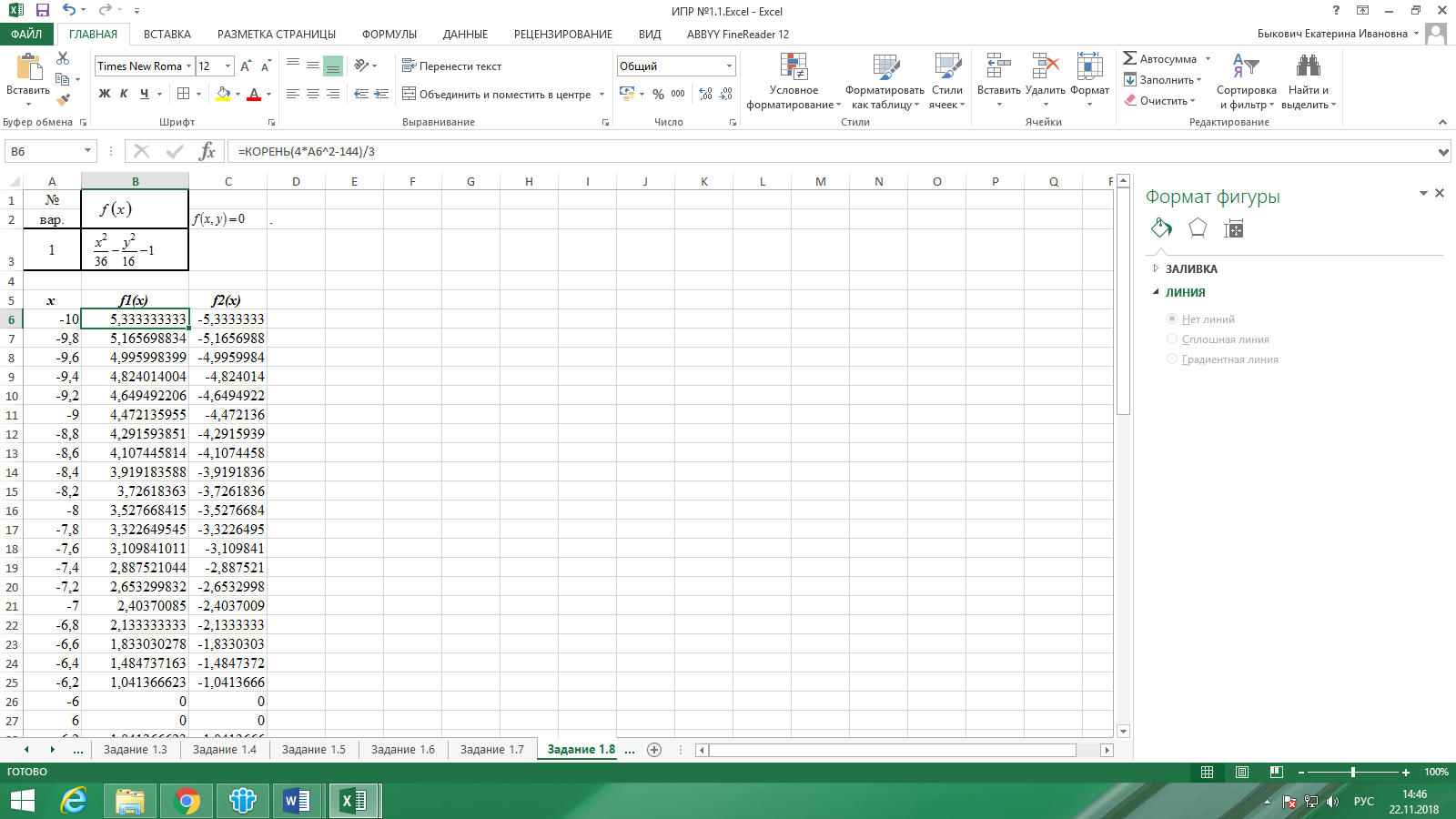
Рисунок 12 Заполнение формы задания 1.8
Выполнив все необходимые действия по построению графика, получим результат, который представлен на рис. 13.
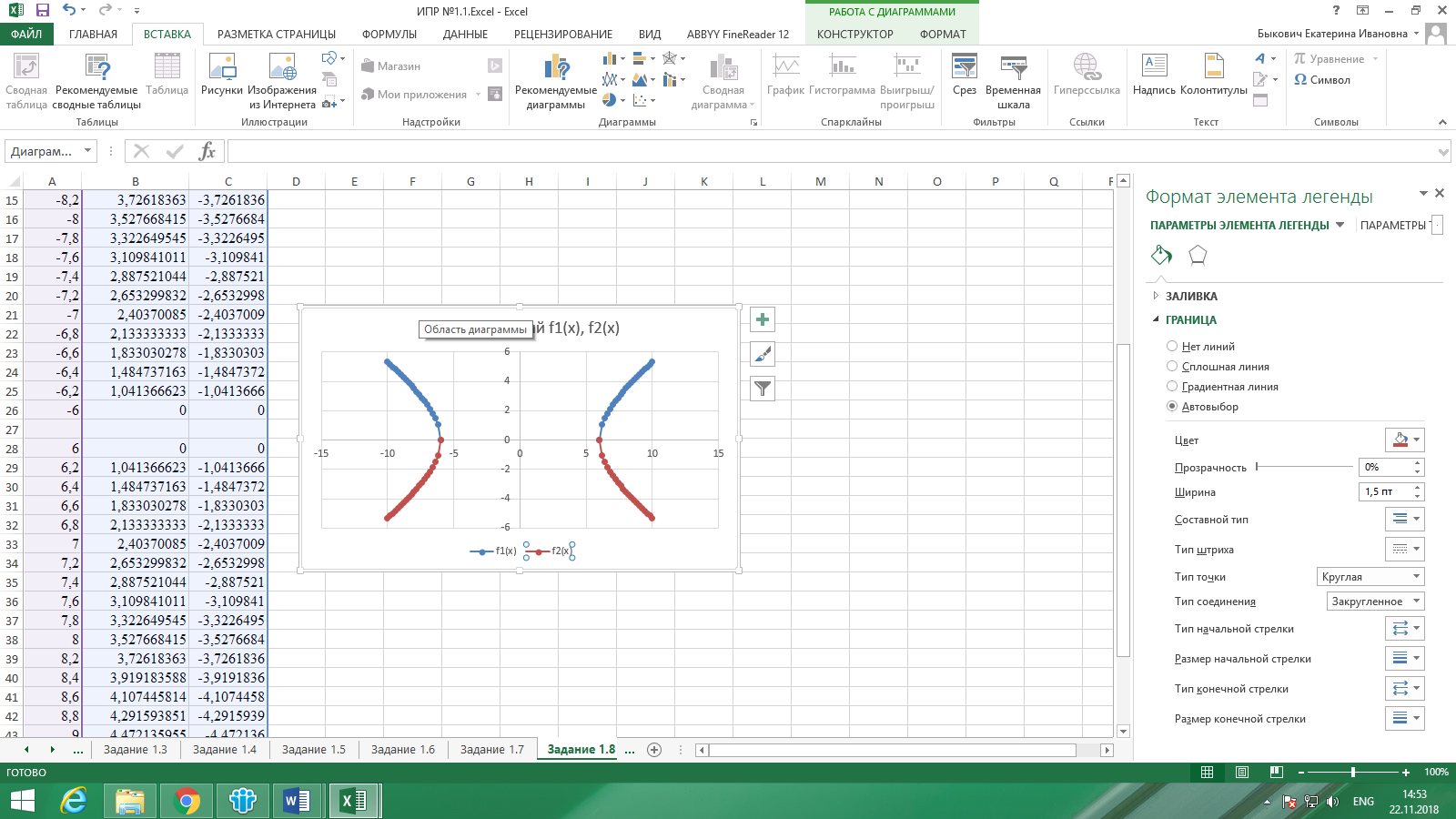
Рисунок 13. Результат выполнения задания 1.8
Задание
2. Построить
в
MS
Excel
поверхность. Построить
в
MS
Excel
нижнюю (нечетные варианты) часть
эллипсоида, заданного уравнением
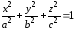 .
.
|
№ вар. |
a |
b |
c |
|
1 |
1 |
2 |
3 |
Для
построения поверхности необходимо
разрешить заданное уравнение относительно
переменной
 .
.
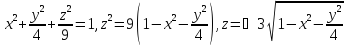
Так как в условии речь идет о нижней части эллипсоида, то рассмотрим ОДЗ отрицательной части уравнения:
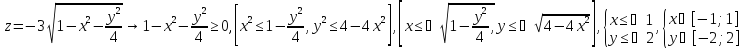
Приступим к построению поверхности. В диапазон B1:J1 введем по-следовательность значений переменной y: -2, -2.5, …,2, а в диапазон ячеек А2:А14 последовательность значений переменой x: -1, -0,5,…1.
В ячейку В2 введем формулу: =(-3)*(1-$A2^2-(B$1^2)/4)^1/2
Заполняем этой формулой диапазон В2:J6.
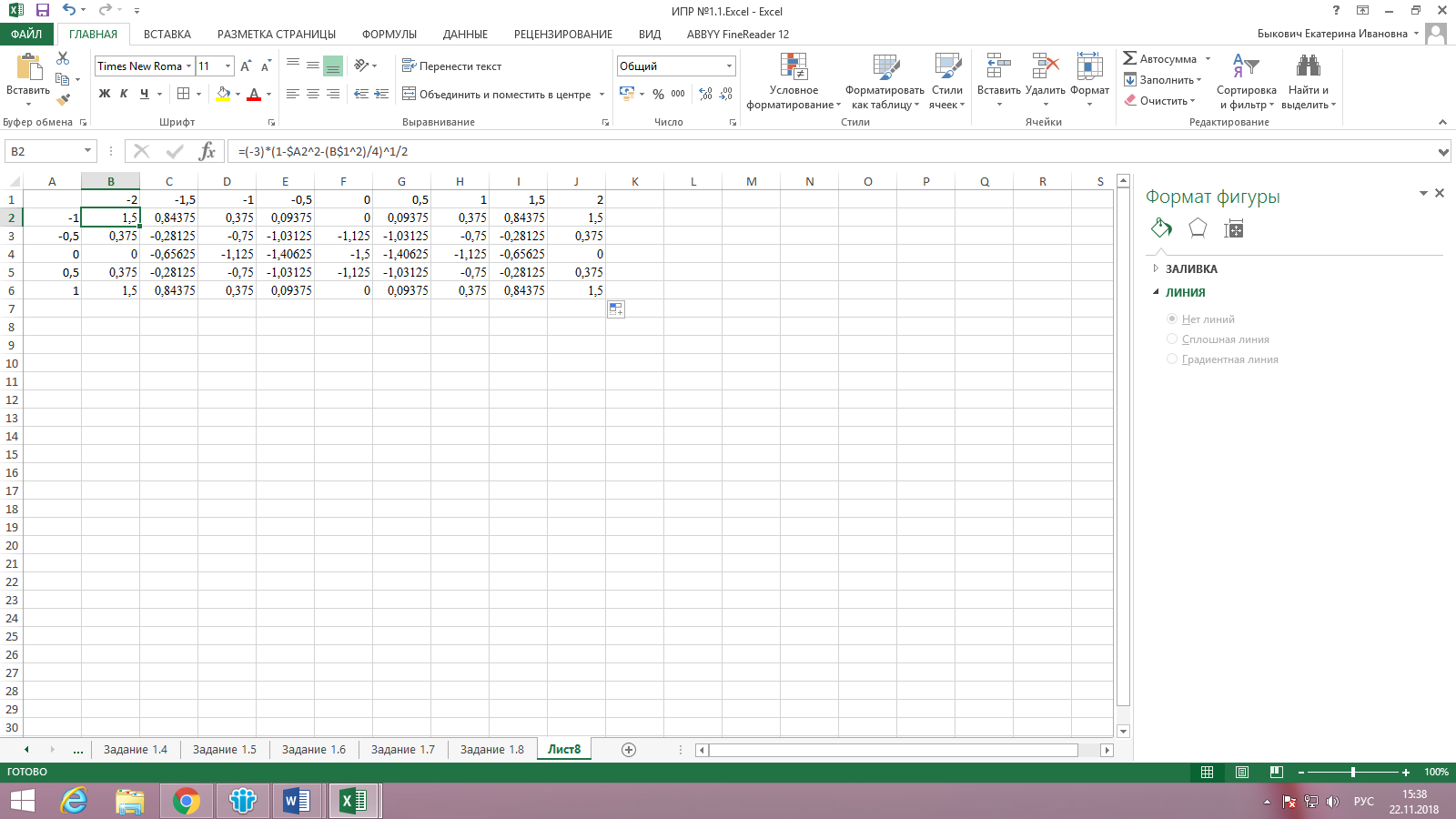
Рисунок 14. Заполнение формы задания 2
Перейдем к построению поверхности. Выделим диапазон ячеек А1:J6, Вставка – Диаграммы – Поверхность. Результат представлен на рис. 15.
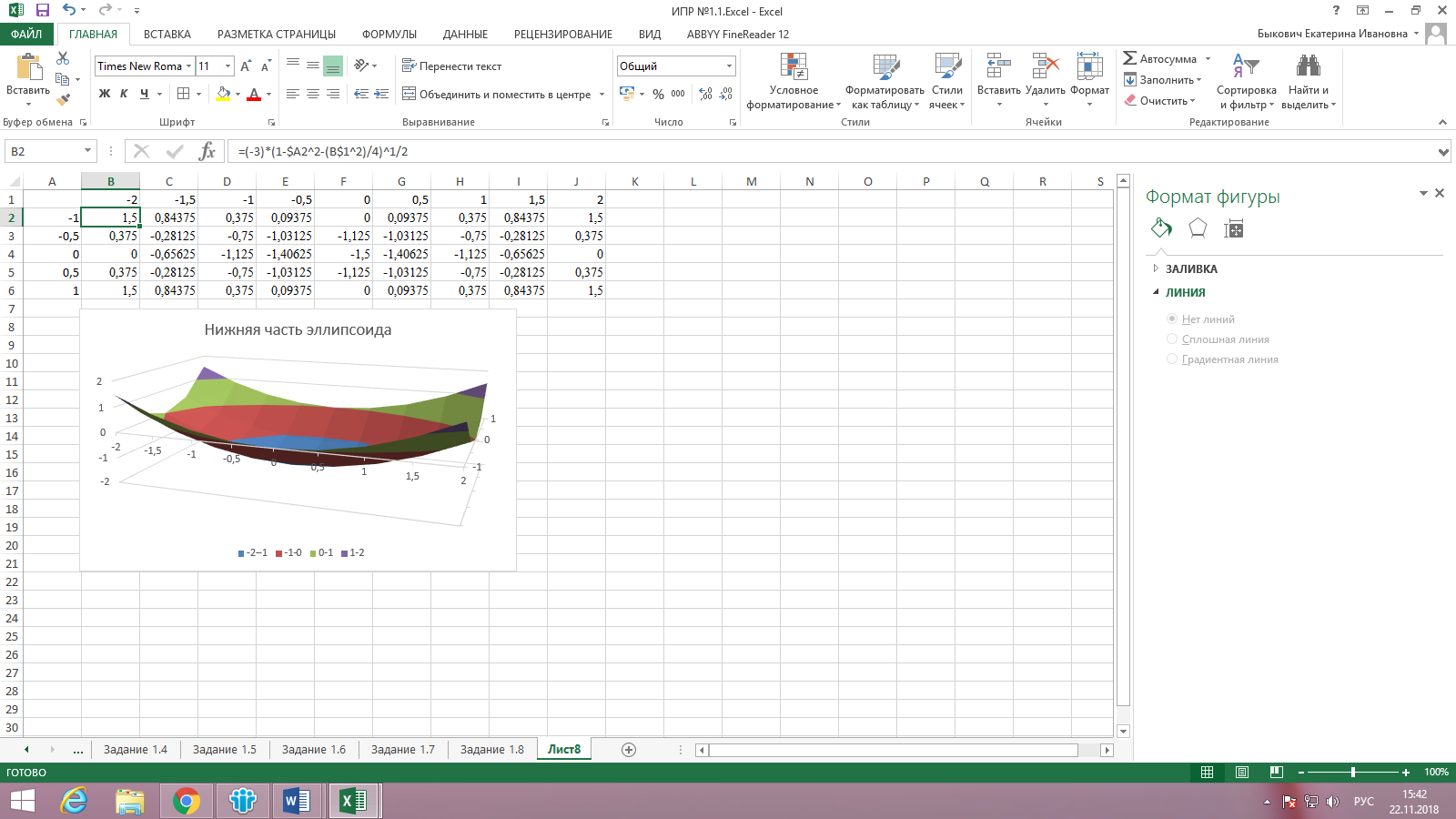
Рисунок 15. Результат задания 2
Задание 3: Выполнить действия над матрицами в соответствии с вариантом.
|
№ варианта |
Задание |
|
1 |
|
На листе введем данные матриц А и В. Сначала произведем сложение матриц.
Выделите ячейки Е6:G8. Введите формулу: =D2:F4+H2:J4.
После введения формулы одновременно нажмите сочетание клавиш CTRL+SHIFT+ENTER.
Далее проведем умножение матрицы А+В на 2; умножим матрицу В на 2; от результата предыдущего выражения отнимем матрицу А. Этих действий нам достаточно, чтобы решить задание (для умножения матриц необходимо использовать формулу МУМНОЖ ()). Результат на рис. 16.
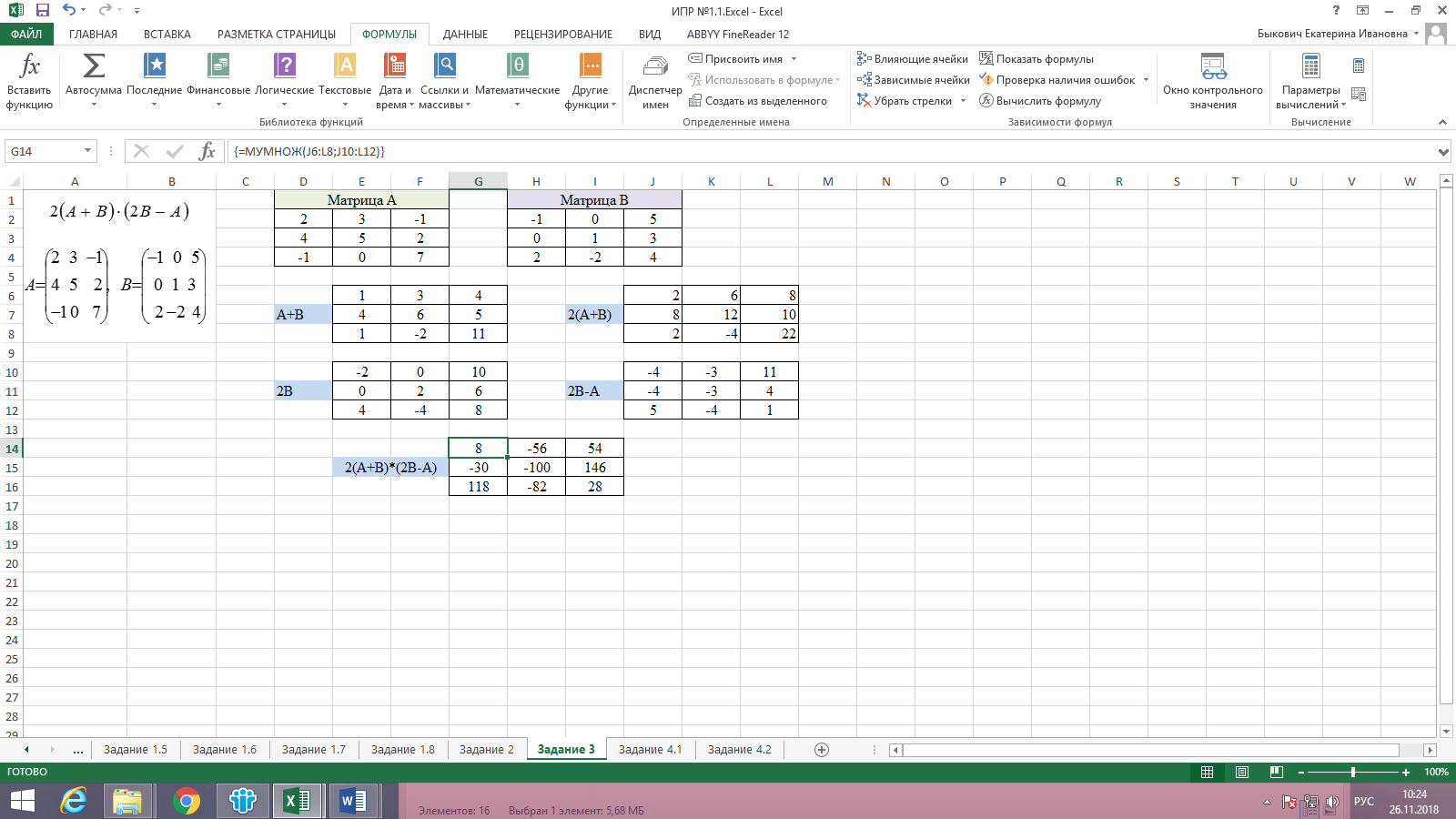
Рисунок 16. Результат задания 3
Задание 4: Решить систему уравнений в соответствии с вариантом. При решении задач руководствоваться тем, что в вариантах предполагается:
1.Решить систему уравнений методом Крамера.
2.Решить систему уравнений с помощью обратной матрицы.
Вариант 1
|
1. |
|
|
2. |
|
1. Введём матрицу А и вектор b на рабочий лист. Кроме того, сформируем четыре вспомогательные матрицы, заменяя последовательно столбцы матрицы A на столбец вектора b (рис. 17).
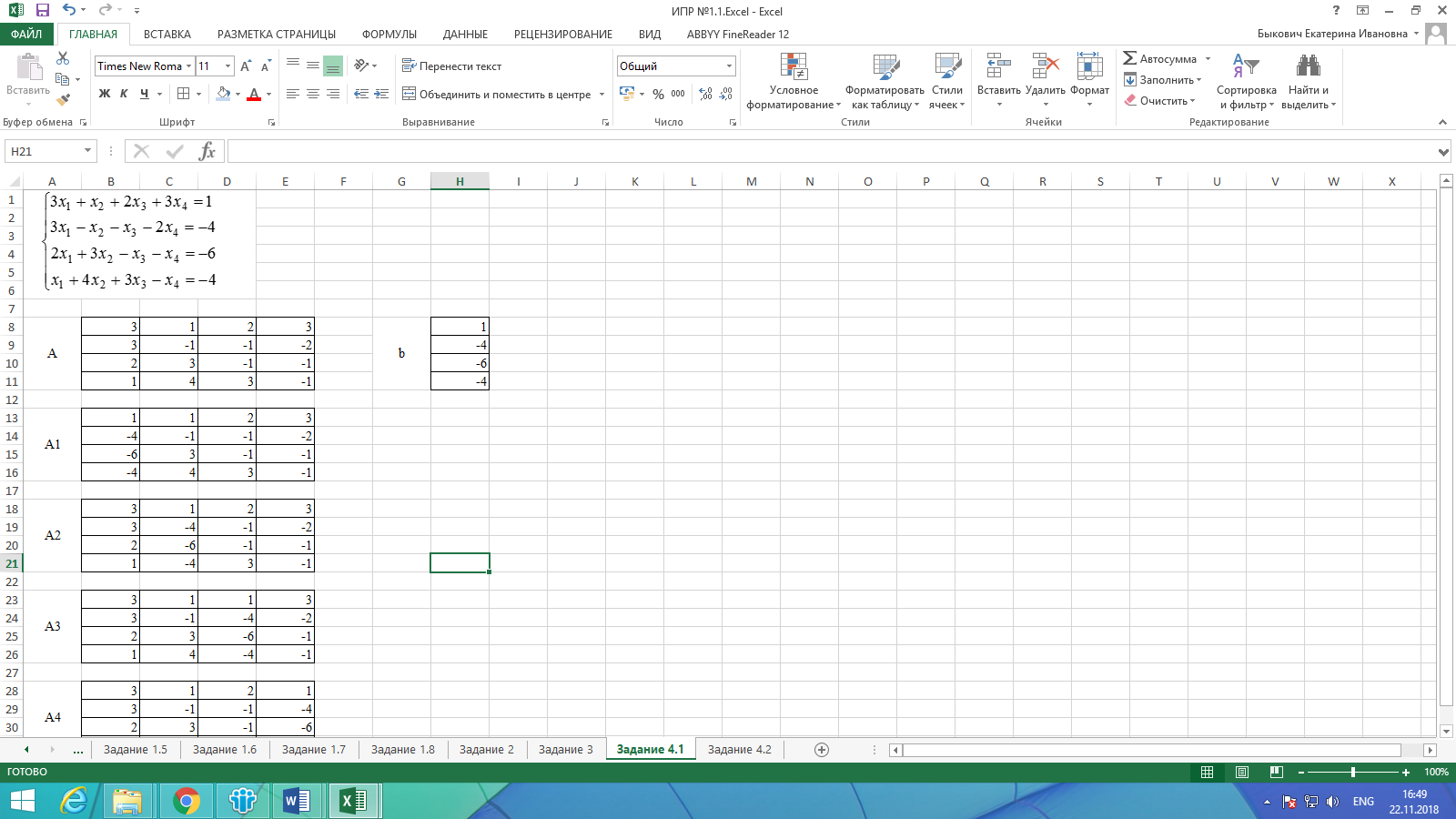
Рисунок 17. Заполнение формы задания 4.1
Для дальнейшего решения необходимо вычислить определитель матрицы A. Установим курсор в ячейку I10 и обратимся к мастеру функций. В категории Математические выберем функцию МОПРЕД, предназначенную для вычисления определителя матрицы, и перейдём ко второму шагу мастера функций. Диалоговое окно, появляющееся на втором шаге содержит поле ввода Массив. В этом поле указывают диапазон матрицы, определитель которой вычисляют. В нашем случае это ячейки B9:E11. Формула =МОПРЕД(B8:E11)
Аналогичные вычисления для вспомогательных определителей.
Воспользуемся формулами Крамера и разделим последовательно вспомогательные определители на главный. В ячейку K11 введём формулу =I11/$I$10. Затем скопируем её содержимое в ячейки K12, K13 и K14. Система решена.
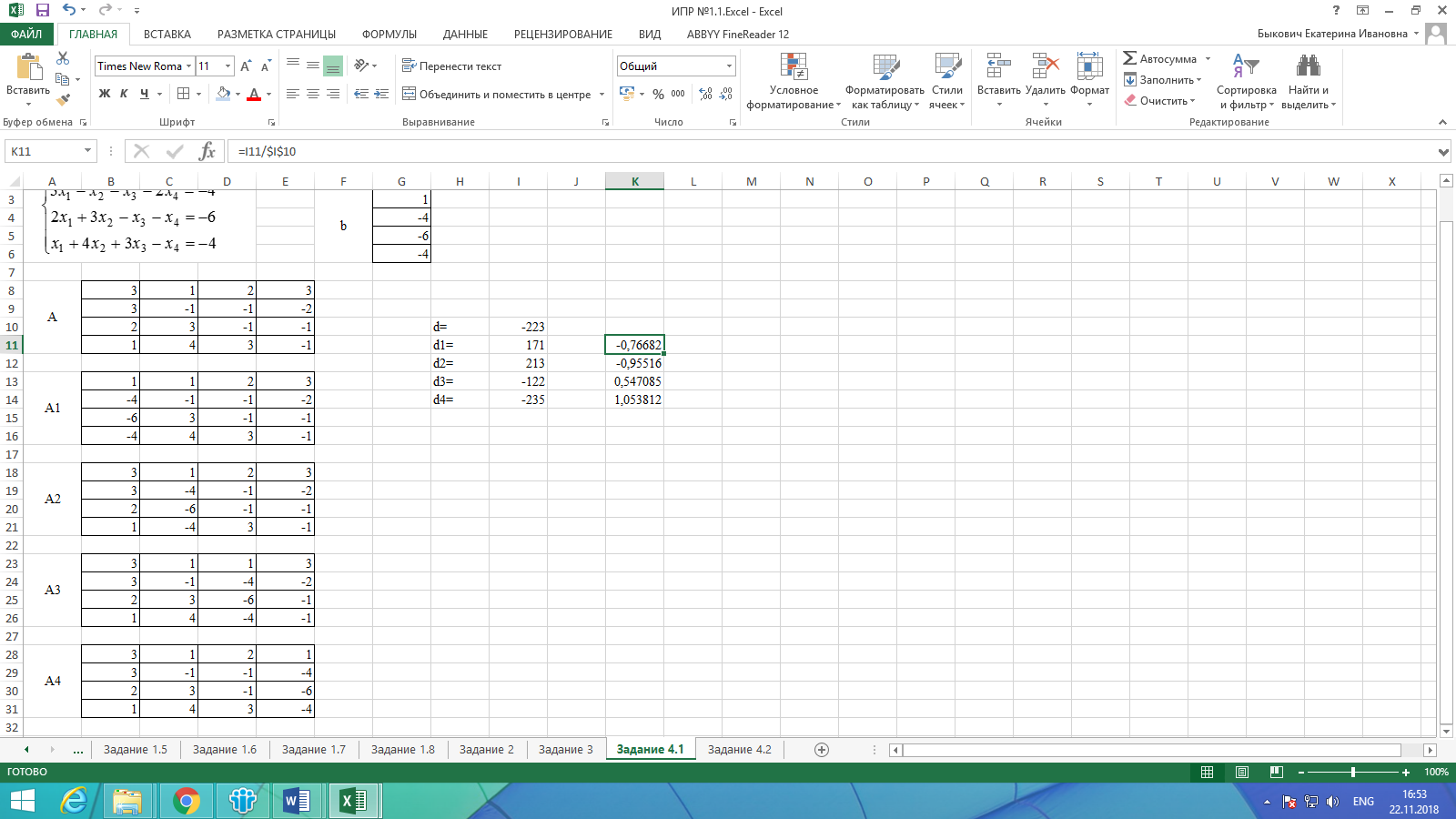
Рисунок 18. Результат задания 4.1
2. На рабочем листе введём матрицу A и вектор b (рис. 19).
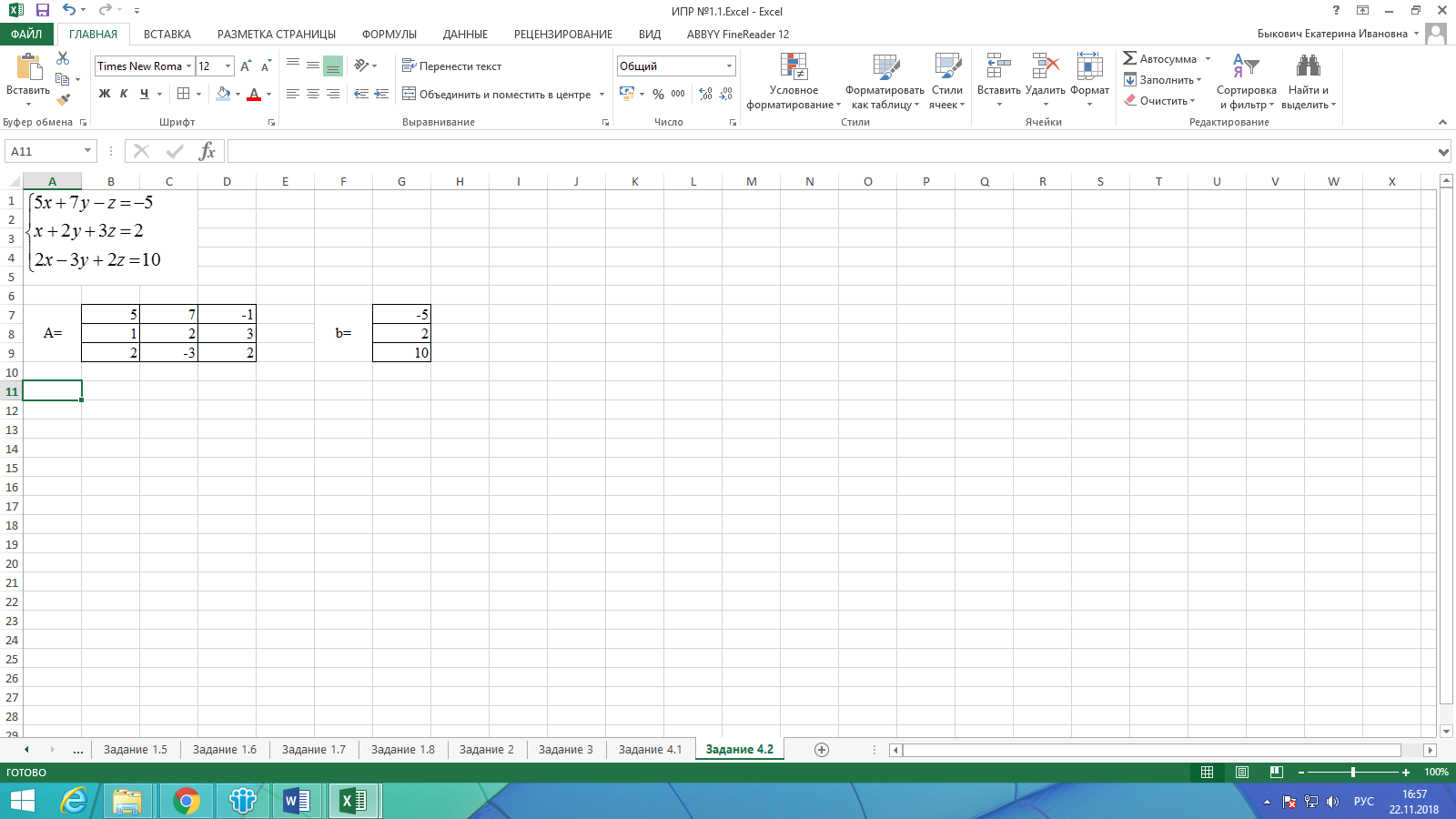
Рисунок 19. Заполнение формы задания 4.2
Для решения системы методом обратной матрицы необходимо вычислить матрицу, обратную к A. Выделяем ячейки В11:D13, теперь обратимся к мастеру функций, и в категории Математические выберем функцию МОБР, выделяем массив B7:D9, ОК. В первой ячейке, выделенного под обратную матрицу диапазона, появится некое число. Для того чтобы получить всю обратную матрицу, необходимо нажать клавишу F2 для перехода в режим редактирования, а затем одновременно клавиши Ctrl+Shift+Enter.
Теперь необходимо умножить полученную обратную матрицу на вектор b. Выделим ячейки для хранения результирующего вектора, например, F11:F13. Обратимся к мастеру функций, и в категории Математические выберем функцию МУМНОЖ, которая предназначена для умножения матриц. В поле Массив1 необходимо ввести диапазон ячеек, в котором содержится первая из перемножаемых матриц, в нашем случае B11:D13 (обратная матрица), а в поле Массив2 ячейки, содержащие вторую матрицу, в нашем случае G7:G9 (вектор b). Если поля ввода заполнены, можно нажать кнопку OK. В первой ячейке выделенного диапазона появится соответствующее число результирующего вектора. Для того чтобы получить весь вектор, необходимо нажать клавишу F2, а затем одновременно клавиши Ctrl+Shift+Enter.
Для того чтобы проверить, правильно ли решена система уравнений, необходимо умножить матрицу A на вектор x и получить в результате вектор b. Умножение матрицы A на вектор x осуществляется при помощи функции =МУМНОЖ(B7:D9;F11:F13), так как было описанной выше.
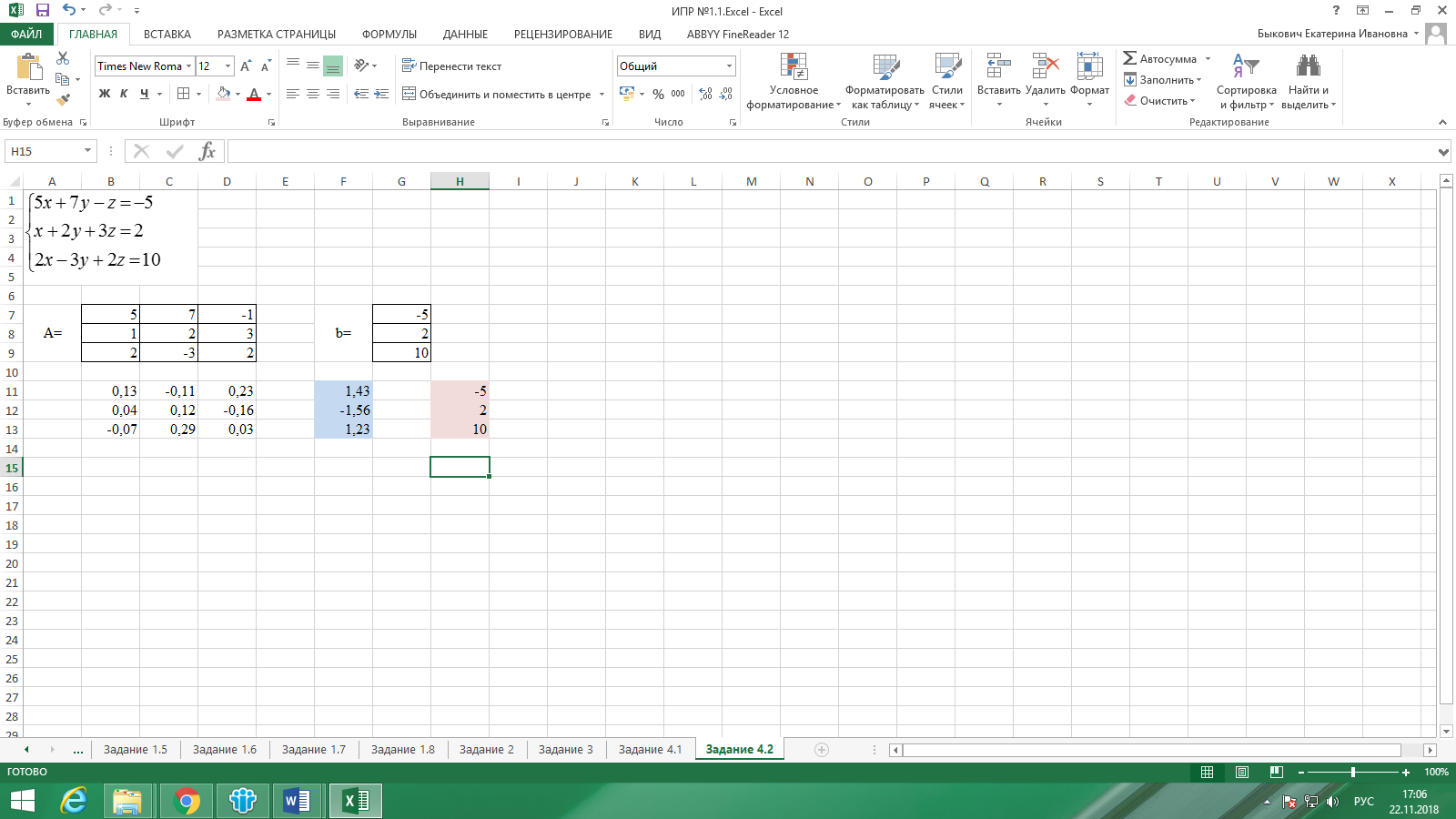
Рисунок 20. Результат задания 4.2

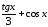

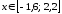
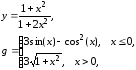
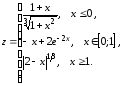
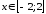
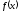
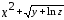
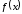
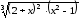
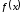
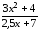
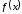
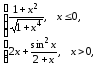
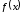
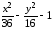
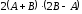 ,
где
,
где